11 Вопрос Векторное уравнение прямой

Положение прямой можно задать по точке и направляющему вектору.

Пусть прямая L задана ее точкой M₀(x₀;y₀;z₀) и направляющим вектором S(m;n;p). Возьмем на прямой L точку M(x;y;z). Обозначим радиус-векторы точек M и M₀ через r и r₀.

Тогда уравнение прямой запишется в виде:

где t – скалярный множитель (параметр).

12 Вопрос Канонические уравнения прямой

S(m;n;p) – направляющий вектор прямой L. M₀(x₀;y₀;z₀) – точка на прямой. соединяет M₀ с произвольной точкой М.

13 Вопрос Общее уравнение прямой

Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:

Т.к. прямая перпендикулярна векторам n₁ и n₂ то направляющий вектор запишется как векторное произведение:

Частные случаи:

     1) By + C = 0 - прямая параллельна оси Ox;

     2) Ax + C = 0 - прямая параллельна оси Oy;

     3) Ax + By = 0 - прямая проходит через начало координат;

     4) y = 0 - ось Ox;

     5) x = 0 - ось Oy.

Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.

Направляющий вектор произвольной прямой в дальнейшем обозначается буквой  , его координаты - буквами l, m, n:

.

Если известна одна точка   прямой и направляющий вектор  , то прямая может быть определена (двумя) уравнениями вида

. (1)

равнение прямой на плоскости: Ах+Ву+С=0

Координаты нормального вектора: (А;В),

14 Вопрос Уравнение прямой с угловым коэффициентом

Если в общем уравнении прямой , то его можно записать в виде уравнения с угловым коэффициентом

где угловой коэффициент, 

a – угол, образованный прямой с положительным направлением оси , – свободный член, равный ординате точки пересечения прямой с осью .

Однозначно определить прямую можно, задав одну точку и угловой коэффициент. А именно, уравнение прямой, проходящей через точку с угловым коэффициентом , определяется по формуле

. (2)

Пример 1. Составить уравнение прямой проходящей через (.)А(-1,2) с угловым коэффициентом .

Решение. Воспользуемся формулой (2), подставив координаты данной точки и угловой коэффициент или общее уравнение .

Ответ: общее уравнение прямой .

15 Вопрос Уравнение прямой в отрезках на прямой

Если в общем уравнении прямой , то разделив (1) на , получаем уравнение прямой в отрезках

,

 

где , . Прямая пересекает ось в точке , ось в точке .

Пример 3. Дано общее уравнение прямой . Записать данное уравнение прямой в отрезках.

Решение. , разделим на 7, запишем . Это уравнение в отрезках. Оно говорит о том, что данная прямая проходит через точки , , т. е. Отсекает на положительной части оси абсцисс , на отрицательной части оси ординат – (-7).

Пример 4. Составить уравнение прямой, отсекающей на осях координат отрезки

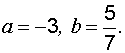
Решение. Уравнение искомой прямой можно записать в отрезках .

Легко можно привести уравнение к общему виду .

Ответ: .