24.6. Дифференциалы высших порядков

Пусть у=ƒ(х) дифференцируемая функция, а ее аргумент х — независимая переменная. Тогда ее первый дифференциал dy=ƒ'(х)dx есть также функция х; можно найти дифференциал этой функции.

Дифференциал от дифференциала функции у=ƒ(х) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается d²y или d²ƒ(х).

Итак, по определению d²y=d(dy). Найдем выражение второго дифференциала функции у=ƒ(х).

Так как dx=∆х не зависит от х, то при дифференцировании считаем dx постоянным:

d²y=d(dy)=d(f'(x)dx)=(ƒ'(х)dx)'•dx=f"(x)dx•dx=f"(x)(dx)² т. е.

d²y=ƒ"(х)dх².                                            (24.5)

Здесь dx² обозначает (dx)².

Аналогично определяется и находится дифференциал третьего порядка

d³y=d(d²y)=d(ƒ"(х)dx²)≈f'(x)(dx)³.

И, вообще, дифференциал n-го порядка есть дифференциал от дифференциала (n-1)-го порядка: dⁿy=d(d^n-ly)=f⁽ⁿ⁾(x)(dx)ⁿ.

Отсюда находим, что , В частности, при n=1,2,3

соответственно получаем:

 

т. е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

 

Отметим, что все приведенные выше формулы справедливы только, если х — независимая переменная. Если же функцию у=ƒ(х), где х — функция от кαкой-mo другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.

Используя формулу дифференциала произведения (d(uv)=vdu+udv), получаем:

d²y=d(f'(x)dx)=d(ƒ'(х))dx+ƒ'(х)•d(dx)=ƒ"(х)dx•dx+ƒ'(х)•d²x, т. е.

d²y=ƒ"(х)dx²+ƒ'(х)•d²x.                               (24.6)

Сравнивая формулы (24.5) и (24.6), убеждаемся, что в случае сложной функции формула дифференциала второго порядка изменяется: появляется второе слагаемое ƒ'(х)•d²х.

Ясно, что если х — независимая переменная, то

d²x=d(dx)=d(l•dx)=dx•d(l)=dx•0=0

и формула (24.6) переходит в формулу (24.5).

<< Пример 24.6

Найти d²y, если у=е^3х и х — независимая переменная.

Решение: Так как у'=3е^3х, у"=9e^3х, то по формуле (24.5) имеем d²y=9e^3xdx².

<< Пример 24.7

Найти d²y, если у=х² и х=t³+1и t— независимая переменная.

Решение: Используем формулу (24.6): так как

у'=2х,    у"=2,    dx=3t²dt,    d²x=6tdt²,

то  d²y=2dx²+2x•6tdt²=2(3t²dt)²+2(t³+1)6tdt²=18t⁴dt²+12t⁴dt²+12tdt²=(30t⁴+12t)dt²

Другое решение: у=х², х=t³+1. Следовательно, у=(t³+1)². Тогда по формуле (24.5)

d²у=у •dt²,

d²y=(30t⁴+12t)dt².

33Теорема Ролля. Если функция y= f(x) непрерывна на отрезке [a; b], дифференцируема во всех внутренних точках этого отрезка (т.е. на (а; b)) и на концах отрезка обращается в нуль f(a) = f(b) = 0, то на (a; b) найдется хотя бы одна точка c  (a; b), в которой f'(c) = 0.

Доказательство. Так как функция f(x) непрерывна на [a; b], то по одной из теорем о непрерывных функциях она достигает на этом отрезке наибольшего значения и наименьшего. Пусть

Заметим, что если М = m, то f(x) = const = 0 (по условию теоремы f(a)=f(b)=0) и, следовательно, f'(x)=0при всех x  [a; b] .

Предположим, что M≠m, тогда, по крайней мере, одно из этих чисел отлично от нуля. Для определенности будем считать, что М ≠0 и М > 0.

Пусть в точке x = c f(c)=М, при этом c≠a и с ≠ b, т.к. f(a)=f(b)=0. Придадим значению c приращение Δx и рассмотрим новую точку c+Δx. Поскольку f(c) – наибольшее значение функции, то f(c+Δx) – f(c)≤0 для любого Δx. Отсюда следует, что

Переходя в этих неравенствах к пределу при Δx→0 и учитывая, что производная при x = c существует, будем иметь:

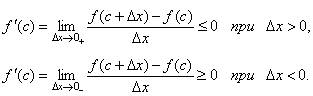
Но неравенства f'(c) ≤ 0 и f'(c) ≥ 0 одновременно возможны лишь в случае, когда

f'(c)=0. Теорема доказана.

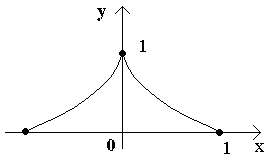
Эта теорема имеет простой геометрический смысл. Если непрерывная кривая, имеющая в каждой точке касательную, пересекает ось Ox в точках x=a и x=b, то на этой кривой найдется хотя бы одна точка с абсциссой c, a < c < b, в которой касательная параллельна оси Ox. Заметим, что доказанная теорема останется справедливой, если предположить, что на концах отрезка функция принимает равные значения f(a)=f(b), не обязательно равные нулю. Кроме того, отметим, что если внутри [a; b] найдется хотя бы одна точка, в которой производная функции f(x) не существует, то утверждение теоремы может оказаться неверным. Пример. Функция непрерывна на [–1; 1], обращается в нуль на концах отрезка. Но производная не обращается в нуль ни в одной точке этого отрезка. 32Теорема Лагранжа. Если функция y= f(x) непрерывна на [a; b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a; b] найдется хотя бы одна точка c, a<c<b такая, чтоf(b) – f(a)=f'(c)(b – a). Доказательство. 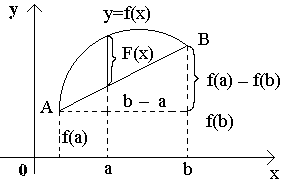Обозначим и рассмотрим вспомогательную функцию F(x) = f(x) – f(a) – k(x – a). Выясним геометрический смысл введенной функции. Для этого рассмотрим график данной функции на [a; b] и напишем уравнение хорды АВ. Заметим, что угловой коэффициент хорды и она проходит через точку A(а; f(a)). Следовательно, ее уравнение y = f(a) + k(x – a). Но F(x)=f(x)–[f(a)+k(x–a)]. ПоэтомуF(x) при каждом x есть разность ординат графика y= f(x) и хорды, соответствующих точкам с одинаковой абсциссой. Легко видеть, что F(x) непрерывна на [a; b] , как разность непрерывных функций. Эта функция дифференцируема внутри [a; b] и F(a)=F(b)=0. Следовательно, к функции F(x) можно применить теорему Ролля. Согласно этой теореме найдется точка c  (a; b), что F'(c)=0. Но F '(x) = f'(x) – k, а значит,F'(c) = f'(c) – k = 0. Подставляя в это равенство значение k, получим , что и требовалось доказать.

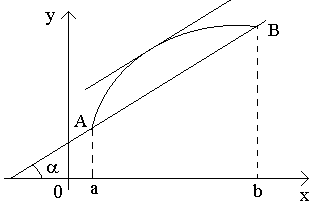
Теорему Лагранжа геометрически можно пояснить так. Рассмотрим график функции y=f(x), удовлетворяющий условиям теоремы и соединим концы графика на [a; b] хордой AB. Как мы уже отметили, отношение для хорды AB, а f'(c) есть угловой коэффициент касательной. Следовательно, теорема утверждает, что на графике функции y=f(x) найдется хотя бы одна точка, в которой касательная к графику параллельна хорде, соединяющей концы дуги.

Теорема Коши. Если f(x) и g(x) – две функции, непрерывные на [a; b] и дифференцируемые внутри него, причем g'(x) ≠ 0 при всех x  (a; b), то внутри отрезка [a; b] найдется хотя бы одна точка c  (a; b), что .

Доказательство.Определим число . Заметим, что g(b) – g(a) ≠ 0, т.к. в противном случае выполнялось бы равенство g(b)=g(a) и по теореме Ролля в некоторой точке d  (a; b)g'(d) = 0. Это противоречит условию теоремы.

Составим вспомогательную функцию.

F(x) = f(x) – f(a) – k[g(x) – g(a)].

Несложно заметить, что F(a)=F(b)=0. Функция F(x) удовлетворяет на [a;b] всем условиям теоремы Ролля. Следовательно, найдется число сÎ(a; b) такое, что F'(c) = 0. Но

F'(x) = f'(x) – k·g(x), а значит F'(c) = f'(c) – k·g'(c) = 0,

откуда .

Заметим, что теорему Коши нельзя доказать, применяя теорему Лагранжа к числителю и знаменателю дроби k. Объясните почему.

ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ

Теорема Ролля. Если функция y= f(x) непрерывна на отрезке [a; b], дифференцируема во всех внутренних точках этого отрезка (т.е. на (а; b)) и на концах отрезка обращается в нуль f(a) = f(b) = 0, то на (a; b) найдется хотя бы одна точка c  (a; b), в которой f'(c) = 0.

Доказательство. Так как функция f(x) непрерывна на [a; b], то по одной из теорем о непрерывных функциях она достигает на этом отрезке наибольшего значения и наименьшего. Пусть

Заметим, что если М = m, то f(x) = const = 0 (по условию теоремы f(a)=f(b)=0) и, следовательно, f'(x)=0при всех x  [a; b] .

Предположим, что M≠m, тогда, по крайней мере, одно из этих чисел отлично от нуля. Для определенности будем считать, что М ≠0 и М > 0.

Пусть в точке x = c f(c)=М, при этом c≠a и с ≠ b, т.к. f(a)=f(b)=0. Придадим значению c приращение Δx и рассмотрим новую точку c+Δx. Поскольку f(c) – наибольшее значение функции, то f(c+Δx) – f(c)≤0 для любого Δx. Отсюда следует, что

Переходя в этих неравенствах к пределу при Δx→0 и учитывая, что производная при x = c существует, будем иметь:

Но неравенства f'(c) ≤ 0 и f'(c) ≥ 0 одновременно возможны лишь в случае, когда

f'(c)=0. Теорема доказана.

Эта теорема имеет простой геометрический смысл. Если непрерывная кривая, имеющая в каждой точке касательную, пересекает ось Ox в точках x=a и x=b, то на этой кривой найдется хотя бы одна точка с абсциссой c, a < c < b, в которой касательная параллельна оси Ox. Заметим, что доказанная теорема останется справедливой, если предположить, что на концах отрезка функция принимает равные значения f(a)=f(b), не обязательно равные нулю. Кроме того, отметим, что если внутри [a; b] найдется хотя бы одна точка, в которой производная функции f(x) не существует, то утверждение теоремы может оказаться неверным. Пример. Функция непрерывна на [–1; 1], обращается в нуль на концах отрезка. Но производная не обращается в нуль ни в одной точке этого отрезка. Теорема Лагранжа. Если функция y= f(x) непрерывна на [a; b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a; b] найдется хотя бы одна точка c, a<c<b такая, чтоf(b) – f(a)=f'(c)(b – a). Доказательство. Обозначим и рассмотрим вспомогательную функцию F(x) = f(x) – f(a) – k(x – a). Выясним геометрический смысл введенной функции. Для этого рассмотрим график данной функции на [a; b] и напишем уравнение хорды АВ. Заметим, что угловой коэффициент хорды и она проходит через точку A(а; f(a)). Следовательно, ее уравнение y = f(a) + k(x – a). Но F(x)=f(x)–[f(a)+k(x–a)]. ПоэтомуF(x) при каждом x есть разность ординат графика y= f(x) и хорды, соответствующих точкам с одинаковой абсциссой. Легко видеть, что F(x) непрерывна на [a; b] , как разность непрерывных функций. Эта функция дифференцируема внутри [a; b] и F(a)=F(b)=0. Следовательно, к функции F(x) можно применить теорему Ролля. Согласно этой теореме найдется точка c  (a; b), что F'(c)=0. Но F '(x) = f'(x) – k, а значит,F'(c) = f'(c) – k = 0. Подставляя в это равенство значение k, получим , что и требовалось доказать.

Теорему Лагранжа геометрически можно пояснить так. Рассмотрим график функции y=f(x), удовлетворяющий условиям теоремы и соединим концы графика на [a; b] хордой AB. Как мы уже отметили, отношение для хорды AB, а f'(c) есть угловой коэффициент касательной. Следовательно, теорема утверждает, что на графике функции y=f(x) найдется хотя бы одна точка, в которой касательная к графику параллельна хорде, соединяющей концы дуги.