31. Статистический и интервальный ряды распределения.

Расположив элементы выборки в порядке не убывания, получим вариационный ряд х₁,х₂,…,х_n. Если в вариационном ряду есть повторяющиеся элементы, то выборку можно записать в виде статистического ряда распределения, т.е. в виде таблицы:

Х	Х’1	X’2	...	X’k
р			...

Для непрерывных случайных величин при достаточно больших объемах выборки n вместо статистического ряда распределения используют интервальный вариационный ряд,

X	[a1;a2)	[a2;a3)	...	[av;av+1)
p			...

Ширина интервала

(где x_(min) – минимальный элемент выборки, х_(max) – максимальный, расчет Δ производится с числом знаков после запятой, на один больше чем в исходных данных). Границы интервалов считаются так: левая граница (л.г.)=х_(min)-0,5Δ; правая граница (п.г.)=(л.г)+Δ

32. Выборочные аналоги функции распределения и функции плотности. Полигон, гистограмма, кумулята.

Выборочным аналогом плотности распределения f_x(x) случайной величины Х служит выборочная плотность распределения . Графиком этой функции является гистограмма – ломанная с вершинами в точках , где через обозначены середины интервалов – полигоном частот, а фигура, состоящая из прямоугольников, в основании которых лежат интервалы группирования (a_j,a_j+1), а высотами являются значения , называется гистограммой. По выборочной плотности распределения легко построить выборочную функцию распределения:

При этом ломанная с вершинами в точках называется кумулятой.

33. Свойства точечных оценок числовых характеристик и параметров распределения.

Статистической оценкой называется любая функция γ=γ(Х₁,Х₂...,Х_n) от элементов выборки Х₁,Х₂,…,Х_n .

Оценка обладающая свойством называется состоятельной оценкой.

Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки .

Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру .

Оценка, обладающая свойством называется эффективной оценкой параметра Θ.

Выборочное среднее является состоятельной, несмещенной и эффективной оценкой математического ожидания МХ.

34. Точечная оценка математического ожидания и ее свойства.

Несмещенная оценка математического ожидания

35. Точечная оценка дисперсии, несмещенная оценка дисперсии.

Смещенной оценкой дисперсии служит выборочная дисперсия

;

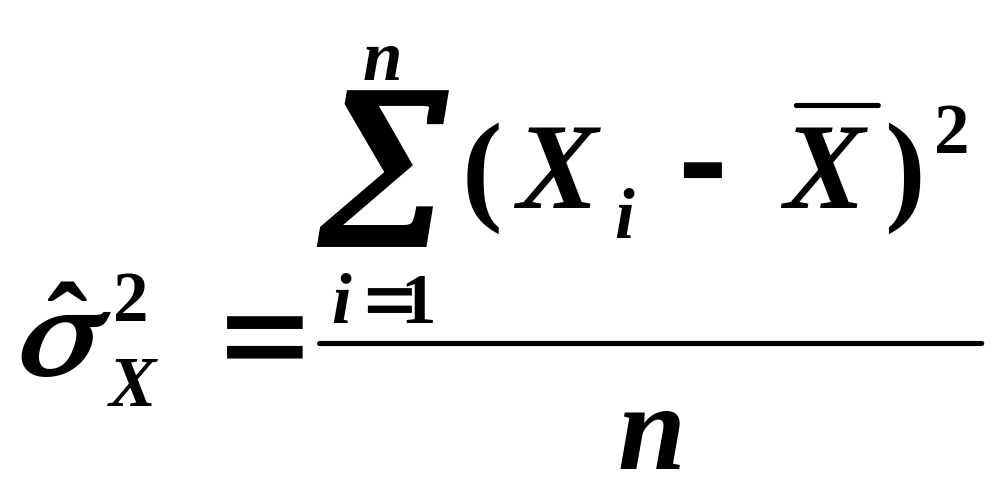Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия

36. Метод моментов. Метод максимального правдоподобия.

Момент – числовая характеристика с.в.

Метод моментов:

1. Определяется зависимость Θ=g(α₁,α₂, …, α_r) параметра Θ от начальных моментов с первого по r-й.

2. Для вычисления оценки параметров Θ по данному методу в эту зависимость g вместо неизвестных теоретических моментов подставляют их выборочные аналоги

Метод наибольшего правдоподобия:

1. Составляется функция правдоподобия:

2. Находится такое значение Θ, при котором эта функция является максимальной, т.е. , и выбирается в качестве оценки.