25. Критерий Вилкоксона.
Данный критерий используется как непараметрический критерий, при любом типе распределения. Критерий Вилкоксона относится к ранговым критериям, причем присваиваемые значения признака могут быть как положительными так и отрицательными. Наблюдения снимают дважды: до эксперимента и после. Под экспериментом понимается некоторое воздействие на объект, в результате которого наблюдаемые показатели могут изменяться в ту или иную сторону. Задачей критерия по статическим данным установить эффективность воздействия. Группа наблюдателей до эксперимента выступает в роли контрольной группы, а группа после эксперимента, в роли экспериментальной группы. В качестве наблюдаемого значения удобно использовать разность наблюдаемых показателей до и после эксперимента для каждого индивидуума. Таким образом из двух групп получается одна выборка значений, среди которых могут быть как положительные так и отрицательные. Затем, чтобы приступить к упорядочиванию выборочных значений, их заменяют соответствующими абсолютными величинами, а затем распределяют по возрастанию. Следовательно, часть рангов будет положительной, а часть других отрицательной. Такие ранги называют знаковыми. Сумма знаковых рангов и есть критерий Вилкоксона.
26. Назовите числовые параметры законов распределения.
Функции распределения являются самым универсальным способом описания поведения результатов измерений и случайных погрешностей. Однако для их определения необходимо проведение весьма длительных и кропотливых исследований и вычислений. В большинстве случаев бывает достаточно охарактеризовать случайные величины с помощью ограниченного числа специальных параметров, основными из которых являются: центр распределения; в начальные и центральные моменты и производные от них коэффициенты — математическое ожидание, СКО, эксцесс, контрэксцесс и коэффициент асимметрии; энтропийный коэффициент.
Координата центра распределения показывает положение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является центр симметрии, т.е. нахождение такой точки Хм на оси х, слева и справа от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5.
Можно определить центр распределения как центр тяжести распределения, т.е. такой точки X̅, относительно которой опрокидывающий момент геометрической фигуры, огибающей которой является кривая р(х), равен нулю:
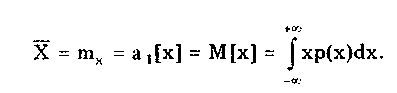
Все моменты представляют собой некоторые средние значения, причем если усредняются величины, отсчитываемые от начала координат, то моменты называют начальными, а если от центра распределения, то центральными. Начальные и центральные моменты г-го порядка определяются соответственно по формулам:
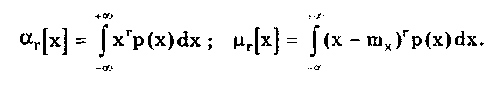
27. Назовите основные классы распределений, используемых в метрологии.
Использование на практике вероятностного подхода к оценке погрешностей результатов измерений прежде всего предполагает знание аналитической модели закона распределения рассматриваемой погрешности. Встречающиеся в метрологии распределения достаточно разнообразны. В качестве примера можно привести результаты исследований фактических распределений погрешностей, имеющих место при измерении электрических и неэлектрических величин разнообразными приборами. Установлено, что примерно 50% распределений принадлежат к классу экспоненциальных, 30% являются уплощенными, а остальные 20% — различными видами двухмодальных распределений. Множество законов распределения случайных величин, используемых в метрологии, целесообразно классифицировать следующим образом: трапецеидальные распределения; уплощеные (приблизительно плосковершинные) распределения; экспоненциальные распределения; семейство распределений Стьюдента; двухмодальные распределения.