21.Методи розв’язування задач динамічного програмування. Основні кроки алгоритму розв’язування задачі динамічного програмування.

22.Метод Франка-Вульфа. Алгоритм розв’язування задачі нелінійного програмування.

Розглянемо метод Франка — Вульфа, процедура якого передбачає визначення оптимального плану задачі шляхом перебору розв’язків, які є допустимими планами задачі.

Нехай необхідно відшукати

за лінійних обмежень:

;

Нехай розв’язок лінійної задачі дав значення цільової функції F0, тоді з точки Х0 в напрямку F0 необхідно рухатись доти, поки не припиниться зростання цільової функції. Тобто у зазначеному напрямку вибирають наступну точку Х1, цільова функція знову замінюється на лінійну, і знову розв’язується задача лінійного програмування.

за умов:

;

.

Нехай розв’язком такої задачі є точка .

З початкової точки в напрямку рухаємося з деяким довільним кроком , визначаючи координати нової точки у такий спосіб:

Зауважимо, що значення параметра доцільно вибирати таким, що дає найбільше значення цільової функції початкової задачі .

Для точки Хk+1 повторюємо розглянутий процес, для чого знову розраховуємо значення градієнта.

23.Модель задачі лінійного програмування в розгорнутому і скороченому вигляді, а також в матричній і векторній формах.

Задачу лінійного програмування зручно записувати за допомогою знака суми «». Справді,задачу можна подати так: за умов: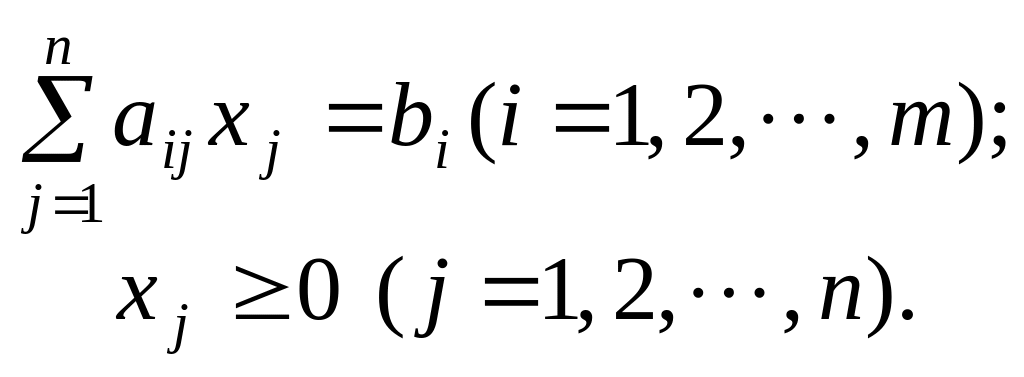 Щекомпактнішим є запис задачі лінійного програмування у векторно-матричному вигляді: max(min) Z = CX max(min) Z = CXза умов: АХ = А₀; Х ≥0,де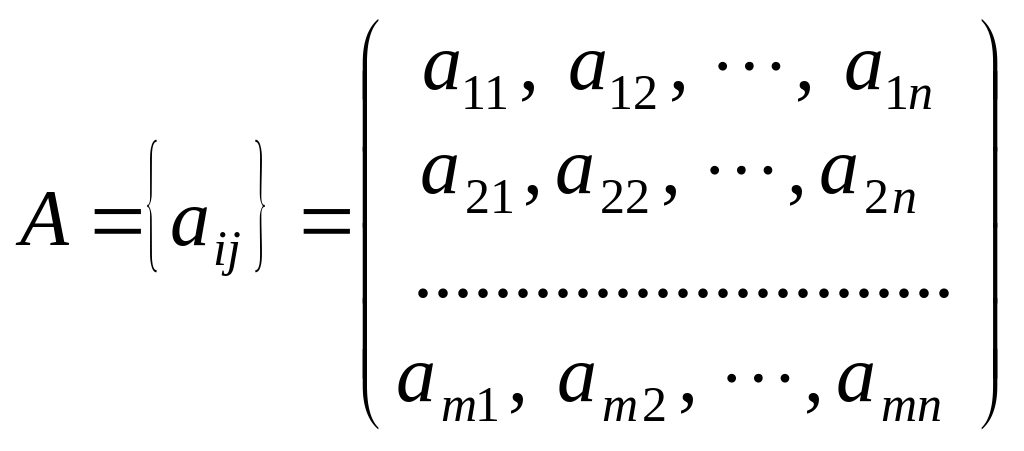 є матрицею коефіцієнтів при змінних;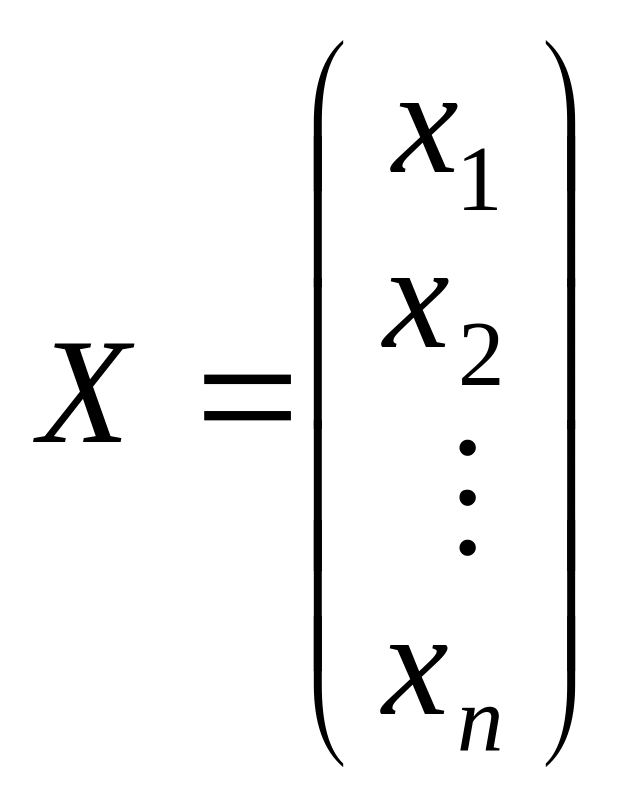 — вектор змінних; 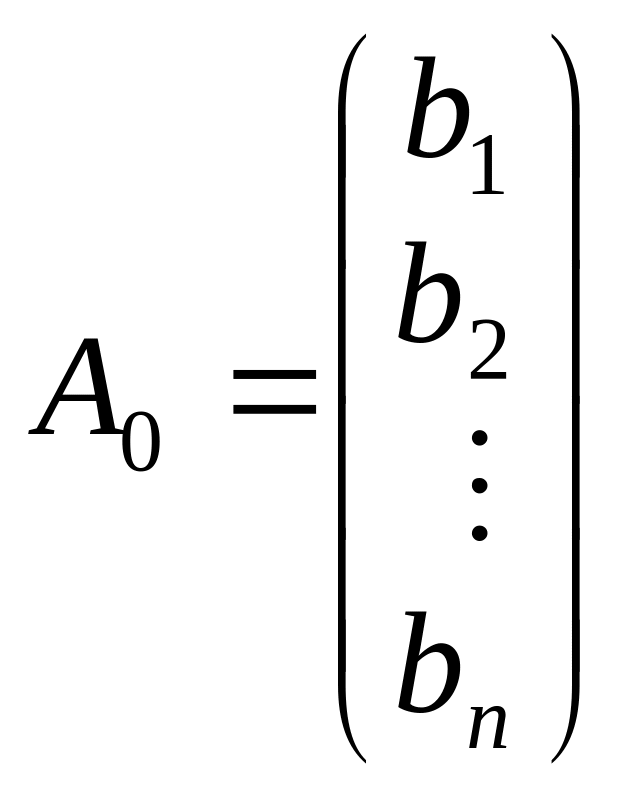— вектор вільних членів;С = (с₁, с₂, …, с_п) — вектор коефіцієнтів при змінних у цільовій функції.Часто задачу лінійного програмування зручно записувати у векторній формі:max(min)Z = CXза умов: A₁x₁ + A₂x₂ + … + A_nx_n = A₀де є векторами коефіцієнтів при змінних.

24.Необхідність використання математичного моделювання економічних процесів.

За цільовим призначенням ЕММ поділяються на теоретико-аналітичні, застосовувані для дослідження загальних властивостей і закономірностей економічних процесів (наприклад, модель Кейнса), та прикладні, призначені для розв’язування конкретних економічних задач (моделі економічного аналізу, прогнозування, управління тощо).

ЕММ можуть бути призначені для дослідження як різних функціональних складових економіки (виробничо-технологічної, соціальної, територіальної структури), так і його окремих частин. Розглядають моделі всієї економіки в цілому та її підсистем — секторів, галузей, регіонів, комплексів моделей виробництва, споживання, формування та розподілу прибутків, трудових ресурсів, ціноутворення, фінансових зв’язків тощо.

Згідно із загальною класифікацією математичних моделей вони поділяються на функціональні та структурні, охоплюючи проміжні форми (структурно-функціональні). У дослідженнях на макрорівні найчастіше використовуються структурні моделі, оскільки для планування та управління велике значення мають взаємозв’язки підсистем. Типовими структурними моделями є моделі міжгалузевих зв’язків. Функціональні моделі широко застосовуються в економічному регулюванні, коли на поводження об’єкта («вихід») впливають, змінюючи «вхід». Прикладом може бути модель поведінки споживачів за умов товарно-грошових відносин. Один і той самий об’єкт може описуватися водночас як структурною, так і функціональною моделлю.