7. Емкостный элемент в цепи синусоидального тока

Емкость отражает явление накапливания энергии электрического поля и характеризуется зависимостью заряда q от напряжения:

Мгновенное значение напряжения на конденсаторе:

Пусть

тогда напряжение на конденсаторе:

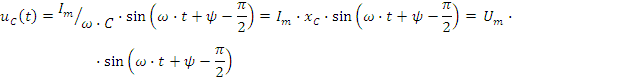
Это напряжение отстает от тока на угол π/2. Векторы тока и напряжения приведены на рис.2.6 б.

Закон Ома для емкости:

где - емкостное сопротивление, измеряется в омах (Ом). Емкостное сопротивление уменьшается с ростом частоты. Зависимость XC от частоты приведена на рис.2.6в. Мгновенная мощность на конденсаторе:

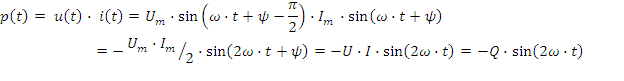
Q- реактивная мощность конденсатора. Временные диаграммы i(t),uC(t),p(t) приведены на рис.2.6г. Среднее значение мощности равно нулю, т.е. рассеивание мощности или потери отсутствуют. Энергия электрического поля в конденсаторе равна:

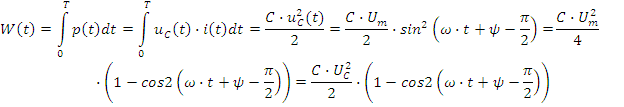
График WC(t) приведен на рис.2.5д. Максимальная энергия электрического поля равна:

Так как:

то

Здесь j⋅xC - емкостное сопротивление в комплексной форме. Закон Ома в комплексной форме:

Векторы ÚC и Í приведены на рис. 2.5е.

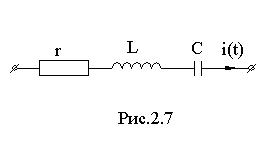
8. Последовательное соединение элементов r, l, c

Для схемы рис.2.7 уравнение по второму закону Кирхгофа для мгновенных значений запишем в виде:

Пусть

тогда:

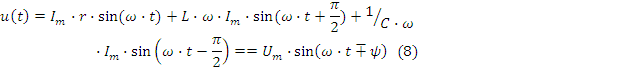
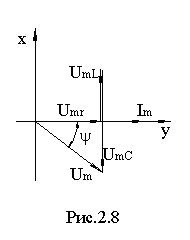
Вектор тока и векторная диаграмма напряжений приведены на рис.2.8 Векторы напряжений на активном и реактивном элементах ортогональны, а векторы напряжений на L и C смещены на π

В комплексной форме уравнение (8) примет вид:

Здесь

На комплексной плоскости сопротивления r, j⋅xL, -j⋅xC, Z – образуют треугольник сопротивления, рис. 2.9.

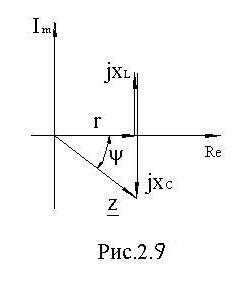
Если сопротивления умножить на Í, получим диаграмму напряжений, рис. 2.10.

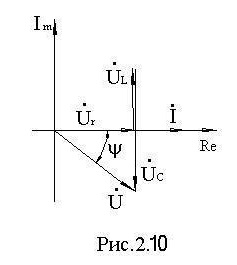
Сравнивая уравнения (8) и (9), отметим, что дифференциальные уравнения (8) после замены мгновенных значений их комплексными символами переводится в уравнение алгебраическое (9). Это одно из преимуществ комплексного метода расчета.Введение понятия комплексного сопротивления, позволяет написать закон Ома для всей цепи в комплексной форме:

Таким образом, для целей переменного тока можно составлять уравнения, по структуре сходной с уравнениями для цепей постоянного тока. В современных условиях контроль над технологическими процессами, потреблением электрической энергии, режимом работы электрооборудования, измерением неэлектрических величин осуществляется с помощью электроизмерительных приборов. Эти приборы измеряют ток, напряжение, мощность, частоту, электрическую энергию и т.д.

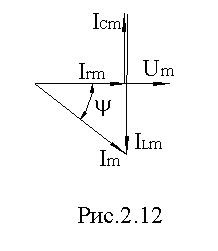
9. Параллельное соединение элементов r, l, c

Для схемы рис.2.11 составим уравнение по первому закону Кирхгофа для мгновенных значений:

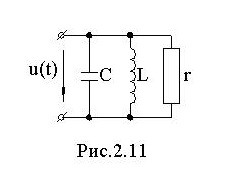
Если

то

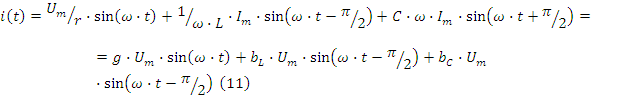
Здесь

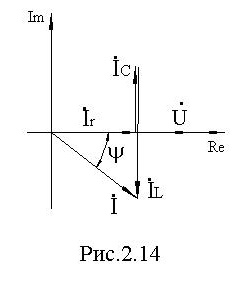
Единица измерения проводимостей - сименс (Сим). Векторная диаграмма токов приведена на рис. 2.12.

Уравнение (11) в комплексной форме:

Здесь

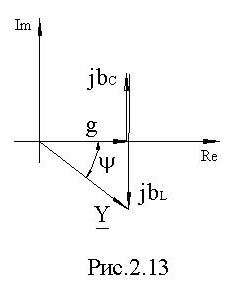
Проводимости g, -j⋅bL, j⋅xC, Y образуют треугольник проводимости, рис. 2.13.

Комплексная векторная диаграмма токов для уравнения (12) приведена на рис. 2.14.