13. Ряды Тейлора и Лорана.

Ряд Лорана по степеням - это формула вида

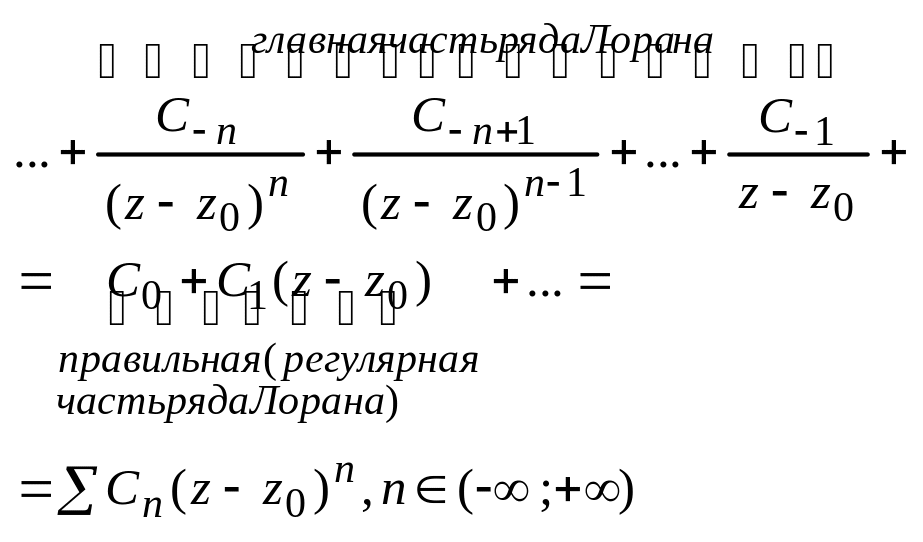
Правильная часть ряда Лорана сходится в круге

Главная часть ряда Лорана сходится в круге , где - внешность круга.

. Если выполняется это условие, то ряд Лорана сходится в кольце .

Теорема Тейлора. Пусть функция является аналитической в точке . Следовательно, , где - ряд Тейлора по степеням . Полученное разложение функции однозначно.

Доказательство.

Теорема Лорана. Пусть функция является аналитической в кольце . Тогда , где - ряд Тейлора по степеням . Полученное разложение функции однозначно.

13. Изолированные точки

Нули ф-ции f(z)=0 наз. изолированными, если их можно окружить непересекающимися окрестностями. Для аналитической ф-ции нули явл. изолированными.

Полюсы.

Предположим, что f(z) аналитична в окрестности z=a, кроме самой точки а, в этом случае точка z=a явл. Изолированной особой точкой ф-ции. В окрестности этой точки f(z) разлагается в ряд Лорана.

Пусть все С_-n равны нулю, тогда. Если перейти к пределу, , но в самой точке ф-ция неопределена. В этом случае точку а наз. устранимой особой точкой ф-ции f(z).

Пусть в главной части ряда Лорана имеется конечное число (к) слагаемых, тогда точка z=a наз. полюсом к-ого порядка. . При z=a С_-к¹0. правую часть обозначим j(z). Функция j(z) явл. Аналитической ф-цией всюду, кроме точки z=a. , где j(z)¹0

. Если для ф-ции f(z) z=a ­ полюс к-ого порядка, то для ф-ции , y(а)¹0, есть ноль к-ого порядка. Справедливо и обратное: если для ф-ции z=a ­ полюс к-ого порядка, w(а)¹0.

Полюсы также явл. Изолированными особыми точками.

Если в разложении (1) главная часть содержит бесконечное число слагаемых, т точка z=a наз. существенно особой точкой.

13. Вычеты.

Если ф-ция аналитическая в какой-то конкр. окрестности z=a, она может быт разложена в ряд Лорана: Особую роль среди коэф-тов играет коэф-т С_-1. Он наз. вычетом ф-ции f(z) в точке z=a. . , где контур g ­ замкнутый контур, окружающий точку z=a и положительно ориентированный. В качестве g можно взят окр. С центром в точке а достаточно малого радиуса (чтобы контур не содержал внутри других особых точек).

.

Вычисление вычетов в полюсе.

Пуст точка z=a явл. полюсом 1-ого порядка. В этом случае разложение в ряд Лорана . Домножим f(z) на z-a

. Переходя к пределу при , получим, что .

13. Основная теорема о вычетах.

Пусть ф-ция f(z) аналитична в некоторой области за исключением крнечного числа особых точек, то согласно теореме (интегр.) Коши для многосвязной области:

. С другой стороны, если интеграл расписать как

.

6 Вопрос § Ортогональные системы вещественных функций

Определение ортогональных функций

Две интегрируемые функций и называются ортогональными на промежутке , если .

Определение ортогональной системы вещественных функций

Система функций называется ортогональной на , если эти функции попарно ортогональны на , то есть , если , .

§ Ряд Фурье по ортогональной системе вещественных функций

Определение ряда по ортогональной системе функций

Пусть – ортогональная система вещественных функций на . Рядом по ортогональной системе вещественных функций называется ряд , где – вещественные коэффициенты.

Теорема о коэффициентах ряда Фурье

Пусть ряд по ортогональной системе вещественных функций равномерно сходится на к функции . Тогда коэффициенты этого ряда имеют вид и называются коэффициентами Фурье.

§ Тригонометрический ряд Фурье

Определение тригонометрического ряда Фурье

Тригонометрическим рядом Фурье называется ряд

Теорема Дирихле (достаточные условия представления функции в виде суммы её ряда Фурье)

Пусть функция f(x ) периодическая, с периодом T=2ℓ; кусочно-непрерывная на любом конечном промежутке [x1, x2] и может иметь разрывы только I рода; кусочно-монотонная. Тогда ряд Фурье, составленный для этой функции, сходится к функции f(x) в каждой точке непрерывности и к среднему арифметическому односторонних пределов в точках разрыва первого рода: ( х0 - точки разрыва I-го рода).

§ Ряд Фурье для чётной и нечётной функции,