4. Основные свойства степенных рядов.
Если
ряда (1), то на (-R;R)
сумма этого рода S
– есть ф-я непрерывная.
Док – во:
Возмем
,
тогда
,
тогда для [-q;q]Î(-R;R)
по теореме Абеля ряд (1) сходится
равномерно. Т. к. x
выбирали
произвольно, то "xÎ(-R;R)
S
– функция
непрерывная.
На интервале сходимости (-R;R) операции почленного диффериецирования и почленного интегрирования не изменяют радиус сходимости.
Док-во.
Пусть
;
- сходится, т. к. –
« -
Если R¹0, то "xÎ(-R;R) ряд (1) можно почленно диффериецировать.
Следствие: степенной ряд можно почленно диффериенцировать сколько угодно раз, при этом R не изменится.
Степенные ряды в (-R;R) можно почленно интегрировать.
5. Ряд Тейлора. Достаточное условие разложимости функции в степенной ряд.
Пусть ф-я f(x) является бесконечно диффериенцируемой, тогда этой ф-и можно поставить в соответствие ряд
Когда x0¹0,
то
В интервале сходимости (-R;R) сумма этого ряда S(x), но не всегда f(x)=S(x).
Если ряд сходится, то его можно представить в виде Sn(x)+rn(x) Pn(x)+Rn(x) и Sn(x)=Pn(x), значит rn(x)=Rn(x) иначе не равны.
Необходимым и
достаточным условием сходимости ряда
(4) к f(x)
является условие
- форма Пеано.
Достаточное условие разложимости функции в степенной ряд. Ряд Тейлора.
Если все производные ограничены одной и той же константой, то ряд Тейлора сходится к ф – и по x.
- сходится по
признаку Даламбера.
У сходящегося общий
член ряда
,
отсюда следует, что
Пусть f(x) бесконечно дифференцируема и
Является
ли этот ряд рядом Тейлора?
………………………………………………………….
.
Пусть x=x0,
тогда
,
или
f(x) – ряд Тейлора.
5.Приближенное вычисление интегралов.
Для вычисления
определенных интегралов
Подинтегральную ф-цию разлагают в ряд Маклорена и в области равномерной сходимости возможно почленное интегрирование
6. Нахождение коэффициентов тригонометрического ряда по формулам Фурье.
Если n и k – целые числа, то
.
6.Интеграл Фурье.
Пусть ф-ция f(x) представлена на отрезке (-l;l)
,
где
;
;
f(x)
абсолютно интегрируема на
,
тогда
*
Ф-ция
, стоящая в правой части явл. Ф-цией от
переменных
.
Устремим
.
Можно показать что если ф-ция f(x)
кусочно-монотонная и ограничена, то
тогда
превращается в следующее (при
)
-интеграл
Фурье.
12. Некоторые основные св-ва интеграла от функции комплексной переменной:
Линейность:
Это св-во обобщается на любое конечное число функций.
При изменении ориентации кривой, по которой берется интеграл, на противоположную, знак интеграла изменяется на противоположный:
.
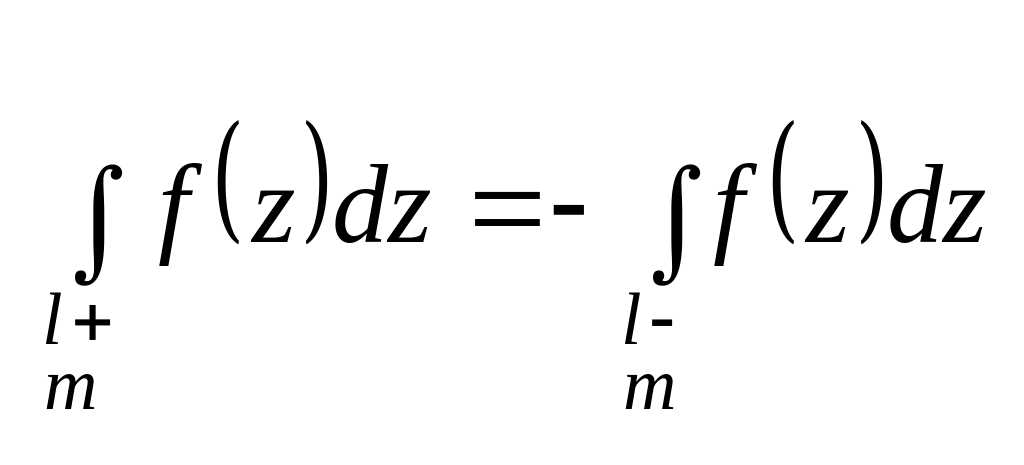Модуль интеграла:
.
12. Интегральная теорема Коши для односвязной области.
Т: Если функция
аналитична в односвязной замкнутой
облости
с границей
,
то
(2)
Односвязная область- область, новые две точки которой можно соединить непрерывной линией, не выходя за эту область. Иначе, область многосвязна,
Док-во (Т):
(поскольку функция
аналитическая и к ней применимо правило
Коши- Римана).
12. Интегральная теорема Коши для многосвязной области.
Т:
-
аналитическая функция в многосвязной
области
с внешней границей
и
-границы
замкнутых контуров внутри области
,
тогда
Док - во:
Приведем в случае трехсвязной области.
Сделаем 2 разреза. Путем их сводим нашу область к односвязной.
Для односвязной
области справедлива интегральная
теорема Коши
Если функция аналитическая, то интеграл от нее не зависит от пути интегрирования.
Если
такова, что интеграл от нее не зависит
от пути интегрирования, то
явл. Аналитической и
(теорема Мереры)
первообразная
для функции
Если
,
то
;
.