Числовые ряды

Числовые ряды являются важным аппаратом, применяемым для вычисления и исследований, как в различных разделах самой математики, так и во многих других.

Понятие числового ряда

Основное определение: Пусть дана бесконечная последовательность чисел a₁, a₂, …, a_n,… Выражение вида

(1)

называют числовым рядом или просто рядом.

Числа a₁, a₂, …, a_n,… называют членами ряда, член a_n с произвольным номером – общим членом ряда. Сумма конечного числа членов ряда

…

называют частичными суммами ряда (1). Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм

(2)

Ряд (1) называется сходящимся, если последовательность его частичных сумм (2) сходится к какому-нибудь числу S

которое в этом случае называется суммой ряда (1). Символически это записывается так:

или

Если последовательность частичных сумм (2) не имеет предела, то ряд (1) называется расходящимся. Расходящийся ряд суммы не имеет.

Пример1: Покажем что ряд

сходится. Возьмем сумму S, первых n чисел ряда

Слагаемые этой суммы могут быть представлены в виде

…

Поэтому

Отсюда следует, сто предел последовательности частичных сумм данного ряда равен единицы:

Таким образом, ряд сходится и его сумма S равна 1.

Основные свойства сходящихся рядов

Если в ряд (1) отбросить конечное число первых членов, например k членов, то получим ряд

(3)

1⁰ . Теорема: Ряд (3) сходится (или расходится ) одновременно с рядом с рядом (1).

Следствие: При исследовании ряда на сходимость можно игнорировать конечное число его первых членов.

2⁰. Теорема: Предел суммы r_k k-го остатка сходящегося ряда (1) при k→∞ равна нулю.

3⁰. Теорема: (необходимый признак сходимости ряда). Общий член a_n сходящегося ряда (1) стремится к нулю при неограниченном возрастании n, т.е.

(4)

Следствие: Если общий член a_n ряда (1) при n→∞ не стремится к нулю, то этот ряд расходится. 4⁰. Теорема: Если ряд (1) сходится и его сумма равна S, то ряд

(5)

где c – произвольное число, также сходится и его сумма равна cS.

Пример 2: Рассмотрим ряд

который называется гармоническим рядом. Поверим, выполняет ли этот ряд необходимое условие сходимости

Предел равен нулю. Значит, необходимое условие сходимости выполняется. Теперь докажем что этот ряд расходится. Если бы этот ряд сходился то, обозначая его сумму через S, мы бы имели

Но

т.е. . Отсюда следует что равенство невозможно, т.е. гармонический ряд расходится.

Таким образом, если общий член ряда стремится к нулю, то еще нельзя сделать вывод о сходимости ряда. Необходимо дополнительное исследование, которое может быть проведено с помощью достаточных условий (признаков) сходимости ряда.

Если же для некоторого ряда его общий член не стремится к нулю, то теорема 4 позволяет сразу сказать, что такой ряд расходится.

Признак сходимости знакоположительного ряда (признак Жамэ)

Теорема: Знакоположительный ряд (a_n ≥ 0) сходится, если при n>n₀, и расходится, если , при n>n₀.

2. Знакочередующиеся ряды. Теорема Лейбница.

Теорема Лейбница:

Если в знакочередующемся ряду , где положительны, члены таковы, что и , то ряд сходится, его сумма положительна и не превосходит первого члена.

Доказательство: Рассмотрим сумму первых членов ряда. По условию 1 выражение в каждой скобке положительно. Следовательно, сумма положительна и возрастает с возрастанием m. Запишем теперь эту же сумму так:

По условию 1 каждая из скобок положительна. Поэтому в результате вычитания этих скобок из мы получим число, меньшее . Таким образом, мы установили, что при возрастании m возрастает и ограничена сверху. Отсюда следует, что имеет предел S

, причем . Однако сходимость еще не доказана. Мы доказали только, что последовательность четных частичных сумм имеет пределом число S. Докажем теперь, что нечетные частичные суммы также стремятся к пределу S. Рассмотрим для этого сумму первых членов исходного ряда. . Так как по условию 2 теоремы , то следовательно Тем самым мы доказали, что как при четном n, так и при нечетном. Следовательно, исходный ряд сходится.

! Теорема Лейбница справедлива, если условия выполняются с некоторого N.

2. Знакопеременные ряды. Абсолютная и условная сходимость.

Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.

Теорема1. Если знакопеременный ряд таков, что ряд, составленный из абсолютных величин его членов сходится, то и данный знакопеременный ряд также сходится.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный ряд называется условно или не абсолютно сходящимся рядом.

3. Функциональные ряды, область сходимости. Равномерная сходимость. Признак Вейерштрассе.

Ряд называется функциональным, если его члены являются функциями от х.

Совокупность тех значений х, при которых функциональный ряд сходится, называют областью сходимости этого ряда.

Функциональный ряд называется равномерно сходящимся на отрезке [a; b], если для любого сколь угодно малого найдется такой номер N, что при всех будет выполняться неравенство для любого х их отрезка [a; b].

Признак Вейерштрассе.

Пусть есть функциональный ряд. Если для него справедливо неравенство и числовой ряд при сходится в некоторой области D, то в этой области ряд сходится равномерно.

3. Основные свойства равномерно сходящихся функциональных рядов.

Непрерывность суммы.

В области равномерной сходимости сумма ряда есть ф-я непрерывная.

Следствие: если функциональный ряд в некоторой области Д сходится равномерно то в этой области возможен предельный переход: .

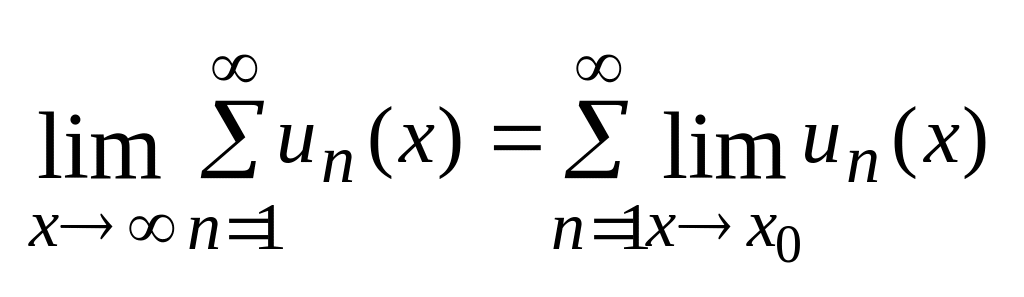В области равной сходимости функциональных рядов их можно почленно интегрировать.

.

Равномерносходящиеся ряды в области равной сходимости можно почленно диффериенцировать.

.

4. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости.

Степенным рядом называется функциональный ряд вида , где - постоянные числа, называемые коэффициентами ряда.

Теорема Абеля.

Если степенной ряд сходится при некотором значении , не равном нулю, то он абсолютно сходится при всяком х, для которого .

Если ряд расходится при некотором значении , то он расходится при всяком х, для которого .

Доказательство: Так как по предположению числовой ряд сходится, то его общий член при , а это значит, что существует такое положительное число М, что все члены ряда по абсолютной величине меньше М. Перепишем ряд в виде и рассмотрим ряд из абсолютных величин его членов:

Члены этого ряда меньше соответствующих членов ряда

При последний ряд представляет собой геометрическую прогрессию со знаменателем и, следовательно, сходится.

Теперь нетрудно доказать и вторую часть теоремы: пусть в некоторой точке ряд расходится. Тогда он будет расходиться в любой точке х, удовлетворяющей условию . Действительно, если бы в какой-либо точке х-, удовлетворяющей этому условию, ряд сходился, то в силу только что доказанной первой части теоремы он должен был бы сходиться и в точке , так как . Но это противоречит условию, что в точке ряд расходится. Следовательно, ряд расходится и в точке х. Теорема полностью доказана.

Интервалом сходимости степенного ряда является такой интервал от –R до R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек х, лежащих вне его, ряд расходится. Число R называют радиусом сходимости степенного ряда.