
- •2. Знакочередующиеся ряды. Теорема Лейбница.
- •2. Знакопеременные ряды. Абсолютная и условная сходимость.
- •3. Функциональные ряды, область сходимости. Равномерная сходимость. Признак Вейерштрассе.
- •3. Основные свойства равномерно сходящихся функциональных рядов.
- •4. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости.
- •4. Основные свойства степенных рядов.
- •5. Ряд Тейлора. Достаточное условие разложимости функции в степенной ряд.
- •13. Ряды Тейлора и Лорана.
- •13. Изолированные точки
- •13. Вычеты.
- •13. Основная теорема о вычетах.
- •6 Вопрос § Ортогональные системы вещественных функций
- •Для функций, заданных на интервале и непериодических функций
- •7. Вопрос Криволинейные интегралы первого рода, их свойства и вычисление
- •7. Поверхностный интеграл первого рода
- •7 Вопрос!!!Криволинейные интегралы
- •8.Вопрос Криволинейный интеграл второго рода
- •8.Поверхностный интеграл второго рода, его свойства
- •9 Вопрос . Формула Грина
- •10 Вопрос. Теория поля
- •1. Скалярное и векторное поле
- •2. Циркуляция векторного поля вдоль кривой
- •3. Ротор векторного поля
- •4. Поток векторного поля
- •5. Дивергенция векторного поля
- •8. Соленоидальные и гармонические векторные поля
- •11 Вопрос Определение функции комплексного переменного.
- •13 Вопрос Вычисление вычетов.
13 Вопрос Вычисление вычетов.
Пусть f(z)
имеет полюс
первого порядка. Тогда она представляется
в виде частного f(z)
=![]() и ряда Лорана
f(z)
=
и ряда Лорана
f(z)
=
![]() +
(z)
. Умножим
f(z)
на (z
– a)
и перейдем
к пределу z
a
+
(z)
. Умножим
f(z)
на (z
– a)
и перейдем
к пределу z
a
lim
f(z)(z – a) = lim
![]() = A-1
(
46 )
= A-1
(
46 )
т.е. вычет функции с полюсом первого порядка в точке а равен пределу произведения функции на двучлен (z – a) при z a .
При вычислении предела в ( 2.17 ) используем правило Лопиталя
lim
= lim
![]() = lim
= lim
![]() =
=
![]() = res f(z) (
47 )
= res f(z) (
47 )
т.е. для определения вычета достаточно значение числителя функции в точке а разделить на значение производной от знаменателя в этой точке
Если f(z) имеет в точке а полюс порядка n, разложение этой функции в ряд Лорана умножим на (z – a)n
(z – a)n f(z) = A-n + A1-n(z – a) + A2-n(z – a)2 + . . . + A-1(z – a)n-1 + (z – a)n (z) ,
(n – 1) раз продифференцируем и получим (n – 1)! А-1 + [(z – a)n (z)](n – 1) . Переход к пределу z a исключит второе слагаемое и определит вычет
res
f(z)
=
![]() lim
lim
![]() (
49 )
(
49 )
Пр. Найти вычеты
функции f(z)
=
![]()
Решение. Полюсами являются точки z = 1 , z = 3
![]() =
=
![]() (z
– 1)
=
(z
– 1)
=
![]() = - ½
= - ½
![]() =
=
![]() (z
– 3)
=
(z
– 3)
=
![]() = 3/2
= 3/2
или по формуле ( 2.18 ) : g(z) = z , h(z) = (z – 1)(z – 3) , h’(z) = 2z – 4 , тогда
=
![]() =
- ½ ;
=
=
- ½ ;
=
![]() = 3/2
= 3/2
Пр. Найти вычеты
функции f(z)
=
![]()
Решение. Здесь z = 2 - полюс третьего порядка, тогда
![]() =
=
![]()
![]()
 =
=
![]() =
2
= 1
=
2
= 1
Вычисление интегралов.
Пусть f(z)
аналитическая
функция в верхней полуплоскости, включая
действительную ось, за исключением n
полюсов ai
расположенных
над осью Ох. Кроме того lim
z2
f(z)
= C
– конечное
число при |z|![]() ,
т.е. на
бесконечности функция становится
двукратной нулевой точкой. Тогда
определенный интеграл
,
т.е. на
бесконечности функция становится
двукратной нулевой точкой. Тогда
определенный интеграл![]() f(x)dx
функции
действительной
переменной
равен
f(x)dx
функции
действительной
переменной
равен
f(x) dx = 2 i ( r1 + r2 + . . . + rn ) ( 50 )
где ri - вычеты функции f(z) в ai . ( 2.20 ) – часть интеграла по замкнутому контуру. Он состоит из действительной оси и полуокружности радиуса R , интеграл вдоль которой равен нулю в силу дополнительного условия.
Пр. Вычислить J
=
![]() .
.
Решение. Функция
f(x)
=
![]() аналитическая в верхней полуплоскости,
за исключением полюса 2 порядка в 2i.
Проверка
дополнительного условия при |z|
аналитическая в верхней полуплоскости,
за исключением полюса 2 порядка в 2i.
Проверка
дополнительного условия при |z|
lim
z2f(z)
= lim
![]() =
lim
=
lim
![]() =
{ z
= r
eit
} = lim
=
{ z
= r
eit
} = lim
![]() =
0
=
0
т.е. конечное число. Вычисление вычета по ( 2.18 )
![]() =
=
![]()
![]()
![]() =
=
![]() =
=
![]() =
=
![]()
Ответ.
J
= 2
i
=
2
i
(
)
=
![]()
Пр. Вычислить J
=![]()
![]() ,
если
-окружности:1)
|z|
= 1, 2)
|z|
= 3, 3)
|z|
= 5
,
если
-окружности:1)
|z|
= 1, 2)
|z|
= 3, 3)
|z|
= 5
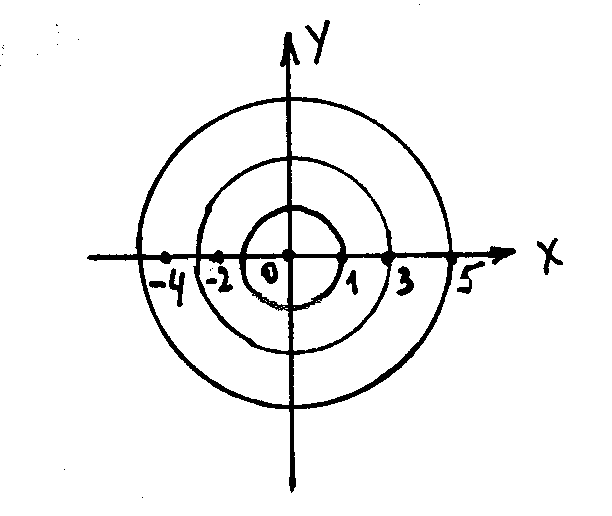
Решение. Найдем вычеты относительно полюсов z = 0 , z = - 2 , z = - 4
 =
=
![]() z
f(z)
=
z
f(z)
=
![]() = 1/8
= 1/8
![]() =
=
![]() (z
+ 2) f(z)
=
(z
+ 2) f(z)
=
![]() = - ¼
= - ¼
![]() =
=
![]() (z
+ 4) f(z)
=
(z
+ 4) f(z)
=
![]() = 1/8
= 1/8
1) Внутри окружности
|z|
= 1 находится
один полюс z
= 0
J1
= 2
i
(![]() )
=
i
/ 4
)
=
i
/ 4
2) Внутри окружности
|z|
= 3 находятся
полюсы z
= 0, z
=-2
J2
= 2
i
(![]() )
= -
i
/ 4
)
= -
i
/ 4
3) Внутри окружности
|z|
= 5находятся
полюсы z
= 0, z
=-2, z
=-4
J3
= 2
i(![]() )=
0
)=
0
