8. Соленоидальные и гармонические векторные поля

Определение 29. Векторное поле A = {A_x, A_y, A_z} называется соленоидальным в области D, если в каждой точке этой области

div A = 0. (121)

Замечание. Так как дивергенция характеризует плотность источников поля А, то в области, где поле соленоидально, нет источников этого поля. Примером соленоидального поля может служить поле точечного заряда е во всех точках, кроме точки, где расположен заряд.

Условием соленоидальности поля является требование, что вектор А является ротором некоторого вектора В: A = rot B. Докажем это.

Действительно, если , то

div A =

=

Определение 30. Скалярное поле, задаваемое функцией u = u(x, y, z), называется гармоническим в некоторой области, если функция и в этой области удовлетворяет уравнению Лапласа: Δ и = 0.

Примеры: линейная функция, потенциал электрического поля точечного заряда или поля тяготения точечной массы.

11 Вопрос Определение функции комплексного переменного.

Опр. Если каждому значению переменной z = x + iy из множества D по правилу f сопоставляется одно или несколько значений w = u + i v из множества W , то f наз. комплексной функцией комплексного переменного (ФКП). D – область определения, W – область значений функции w = f(z).

Функция наз. однозначной, если каждому значению z ставится в соответствие одно значение w и многозначной в ином случае.

Е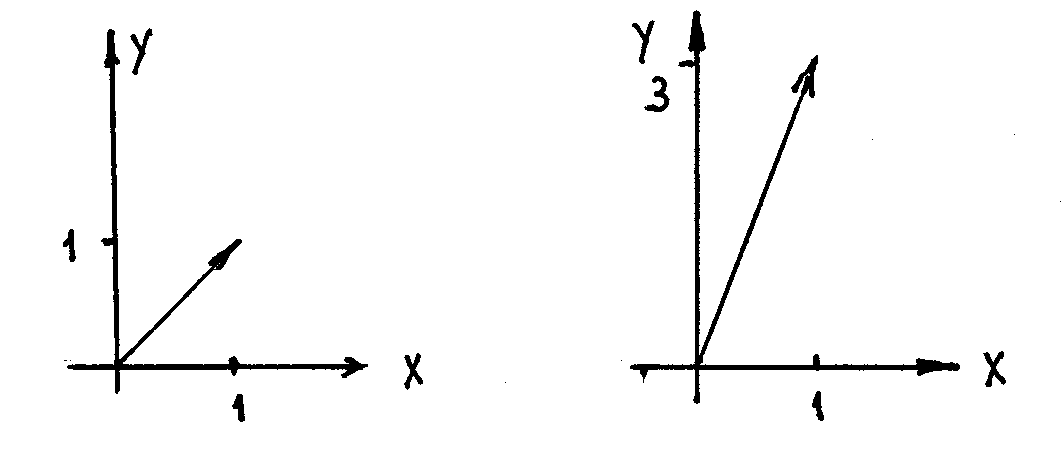 сли w = u + i v есть функция от z = x + iy , то u и v являются действительными функциями от х, у, и наоборот, всякое выражение w =u(x,y)+i v(x,y) есть ФКП от z =x + iy. ФКП w = u(x,y) + i v(x,y) имеет условную запись w = f(z) , которая не означает, что функция зависит от х и у только в комбинации x + i y. Пр. Выражение x + 2i y является функцией переменной z = x + i y.

Пр. Дана функция w = z² + z .

Найти её значение при z = 1 + i .

Решение. w = (1 + i)² + (1 + i) = 1 + 3i .

f

(1 + i) (1 + 3i)

Функция наз. ограниченной, если ее модуль |w| = не превосходит некоторого конечного числа. Предел функции lim f(z) = a при z z₀ складывается из пределов функций u(x,y), v(x,y) при (x,y) (x₀,y₀). Функция f(z) непрерывна в точке z , если функции u(x,y), v(x,y) непрерывны в этой точке.

Принципиально новый момент – геометрический смысл ФКП. Т.к. функция f(z) сопоставляет каждой точке z одной плоскости точку w другой плоскости, то её геометрический смысл - отображать плоскость z в плоскость w .При этом линии и фигуры, описанные изменяющейся z , переходят в линии и фигуры совершенно другой конфигурации.

Имеем некоторую кривую F(x,y) = 0 и ФКП w = u(x,y) + i v(x,y). Надо найти отображение этой кривой на плоскость uOv. Переход к новой системе координат определяют уравнения u = u(x,y), v = v(x,y) . Совершим обратное преобразование

x = x(u,v), y = y(u,v) и перейдем в уравнении кривой к новым переменным

F(x(u,v), y(u,v)) = 0 . Это уравнение определяет отображение исходной кривой.

Пр. В какую кривую отображается окружность |z| = с помощью функции w = z²?

Решение. Имеем окружность x² + y² = 2 и w = (x + i y)² = ( x² – y²) + 2xy i . Получаем систему уравнений перехода к новым координатам u = x² – y² , v = 2xy. Оба уравнения возведем в квадрат и сложим u² + v² = (x² + y²)² x² + y² = . Заменим переменные в уравнении окружности и получим u² + v² = 4 , т.е. окружность |w| = 2 , причем, при прохождении исходной окружности вторая проходится дважды.

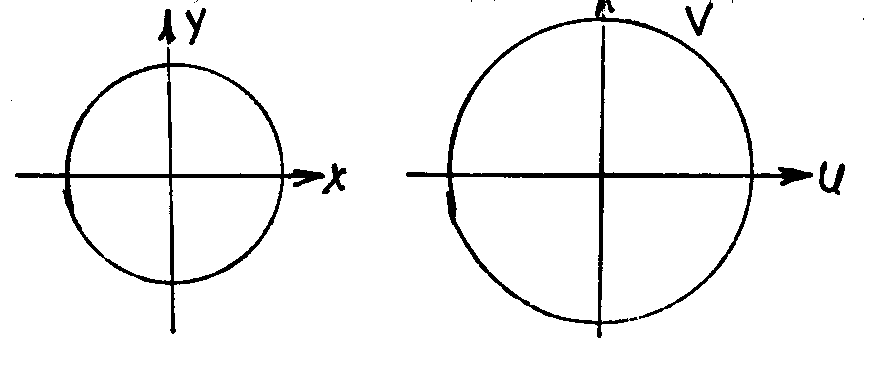
|z| = e^it , (0 < t < 2 ),

w = z² = 2 e^{i 2t}

Элементарные функции комплексной переменной.

Основные элементарные функции для КП подлежат переопределению. Наиболее просто вводится степенная функция по формуле Муавра

zⁿ = (x + i y)ⁿ = rⁿ( cos n + i sin n )

т.е. Re zⁿ = rⁿ cos n , Im zⁿ = rⁿ sin n , r = , arg zⁿ = n .

Действительные функции e^x, sin x, cos x, sh x, ch x представим в виде степенных рядов и заменим в них x на z .

e^z = 1 + z + ( 1 )

sin z = z - ( 2 )

cos z = 1 - ( 3 )

sh z = = z + ( 4 )

ch z = = 1 + ( 5 )

Эти ряды абсолютно сходятся на всей комплексной плоскости, т.к. сходятся ряды из |z| . Cравнение рядов дает простые соотношения для функций. Заменим в ( 1 ), ( 2 ), ( 3 ) z на iz . Тогда из ( 1 ) получаем формулу Эйлера (1743 г.)

e^{i z} = 1 + i z - = cos z + i sin z ( 6 )

а в ( 2 ) и ( 3 ) все слагаемые примут положительный знак и получим

cos iz = ch z , sin iz = i sh z ( 7 )

Соотношения ( 7 ) после замены z на iz принимают вид

ch iz = cos z , sh iz = i sin z ( 8 )

Для КП справедливы формулы

,

sin(z₁ + z₂) = sin z₁ cos z₂ + cos z₁ sin z₂ ( 9 )

cos(z₁ + z₂) = cos z₁ cos z₂ - sin z₁ sin z₂

Для гиперболических функций имеются соотношения аналогичные ( 9 ) и основное тождество ch²z - sh²z = 1 ( 10 )

Определим свойства функций ( 1 ) - ( 5 ) .

Функция e^z e^z = e^{x + i y} = e^x e^{i y} = e^x ( cos y + i sin y ) ( 11 )

т.е. Re e^z = e^x cos y , Im e^z = e^x sin y , | e^z | = e^x , y – аргумент, его главное значение arg e^z = y + 2k , где целое число k определяется условием - < y + 2k < .

При перемещении вдоль мнимой оси функция e^z периодическая, период 2 i ,

Функция sin z Используем формулы ( 9 ), ( 7 ), ( 10 )

sin z = sin(x + i y) = sin x cos iy + cos x sin iy = sin x ch y + i cos x sh y ( 12 )

т.е. Re sin z = sin x ch y , Im sin z = cos x sh y , arg sin z = arctg [ ctg x th y ],

|sin z| = [sin²x ch²y + cos²x sh²y ]^1/2 = [sin²x(1+ sh²y) + cos²x sh²y ]^1/2 =

При перемещении вдоль действительной оси функция sin z периодическая, период 2 .

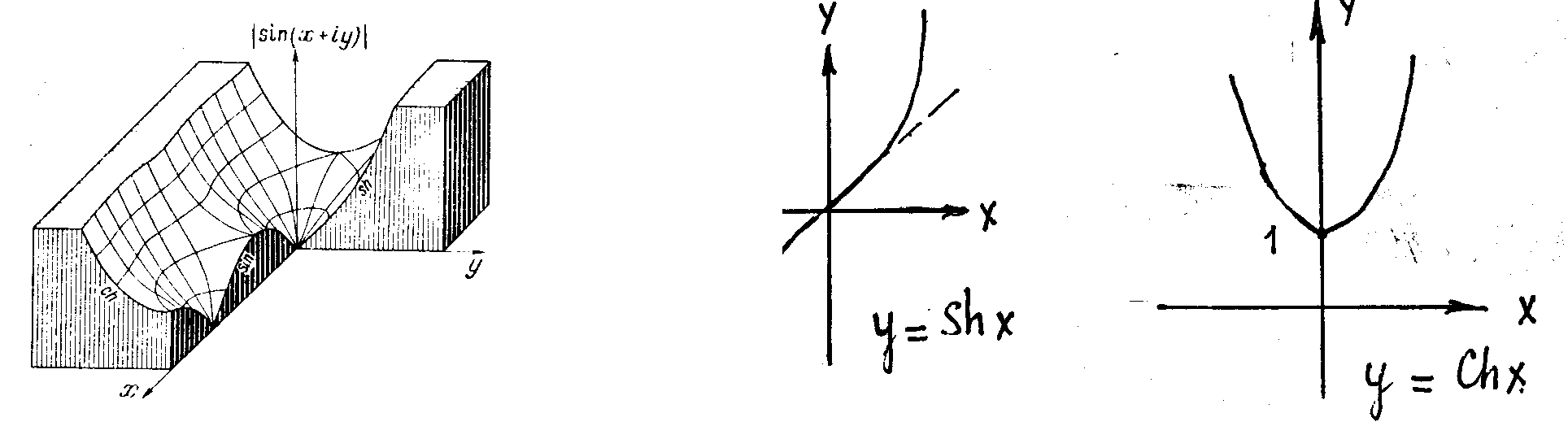
Функция cos z Используем формулы ( 9 ), ( 7 ), ( 10 )

cos z = cos(x + i y) = cos x cos iy - sin x sin iy = cos x ch y - i sin x sh y ( 13 )

т.е. Re cos z = cos x ch y , Im cos z = - sin x sh y , arg cos z = arctg [ - tg x th y ],

|cos z| = [cos²x ch²y + sin²x sh²y ]^1/2 =

При перемещении вдоль действительной оси функция cos z периодическая, период 2 .

Функция sh z Используем формулы ( 9* ), ( 8 ), ( 10 )

sh z = sh(x + i y) = sh x ch iy + ch x sh iy = sh x cos y + i ch x sin y ( 14 )

т.е. Re sh z = sh x cos y , Im sh z = ch x sin y , arg sh z = arctg [ ctg x th y ],

|sh z| = [sh²x cos²y + ch²x sin²y ]^1/2 =

При перемещении вдоль мнимой оси функция sh z периодическая, период 2 i ,

Функция ch z Используем формулы ( 9* ), ( 8 ), ( 10 )

ch z = ch(x + i y) = ch x ch iy + sh x sh iy = ch x cos y + i sh x sin y ( 15 )

т.е. Re ch z = ch x cos y , Im ch z = sh x sin y , arg ch z = arctg [ th x tg y ],

|ch z| = [ch²x cos²y + sh²x sin²y ]^1/2 =

При перемещении вдоль мнимой оси функция ch z периодическая, период 2 i ,

Функции tg z, ctg z, sh z, ch z определяют формулы

Функция ln z Натуральный логарифм числа z = r( cos + i sin ) есть КЧ (x + i y), удовлетворяющее равенству

e^{x + i y} = r ( cos + i sin ) или e^x ( cos y + i sin y ) = r ( cos + i sin )

Откуда следует e^x = r или x = ln r , y = + 2k , т.е.

Ln [ r ( cos + i sin ) ] = ln r + i( + 2k ) ( 16 )

Логарифм КЧ равен логарифму его модуля плюс i , умноженное на одно из значений аргумента.

Общая показательная функция a^z является многозначной a^z = e^{z ln a} ( 17 )

Функция arcsin z Прямую функцию z = sin w = умножим на 2i e^{i w} и получим квадратное уравнение e^{2i w} - 2i e^{i w} - 1 = 0 . Его решение e^{i w} = iz + прологарифмируем и получим

w = arcsin z = -i ln(iz + ) ( 18 )

Аналогично вычисляются: arccos z = -i ln(z + ) , arctg z = ( 19 )

Производная ФКП.

Производная однозначной ФКП w = f(z) определяется как предел отношения приращения функции к приращению аргумента

lim = при ( 20 )

Если предел существует и не зависит от способа стремления к нулю, то функция

w = f(z) наз. аналитической в окрестности точки z .

Определим условие независимости предела ( 20 ) от способа стремления к нулю. Процесс определяют два процесса и . Их относительная скорость h может быть различной. Представим отношение = как функцию от h и определим условие обращения этой функции в константу.

Заменим в отношении на дифференциалы и затем перейдем к пределу

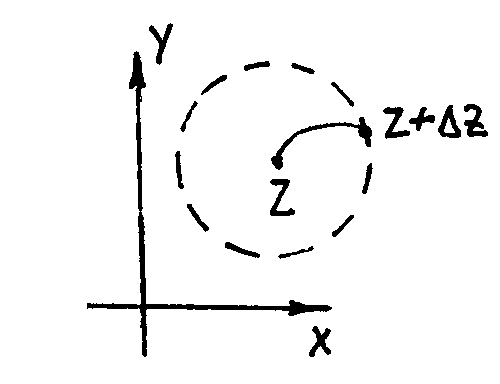
du = u`<sub>x</sub> dx + u`_y dy , dv = v`<sub>x</sub>dx + v`_ydy

= =

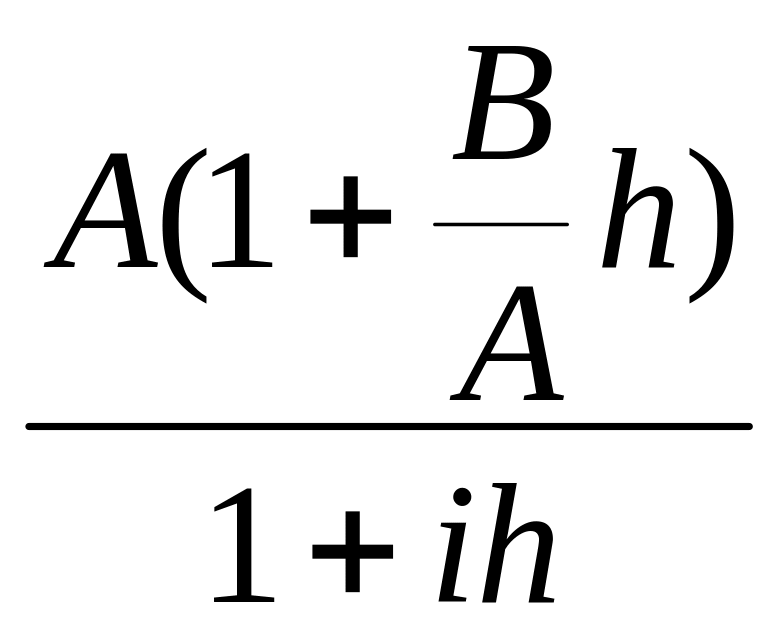Независимость производной от h выполняется при B = i A или u`<sub>y</sub> + iv`_y = i(u`<sub>x</sub> + iv`_x)

Отсюда следуют необходимые условия дифференцируемости Коши – Римана

, ( 21 )

Если частные производные от u и v непрерывны в области D и выполняется условие Коши – Римана, то функция w = f(z) дифференцируема в этой области.

Поскольку частные производные связаны между собой, то выражение для полной производной имеет разные формы

= А = = = = ( 22 )

Пр. Проверим аналитичность функции w = z* по формулам ( 20 ) и ( 21 ). Пусть движение от точки z + z к точке z идет по кривой y = g(x). Тогда при

lim = lim = lim =

т.е. предел отношения приращений функции и аргумента включает тангенс угла наклона касательной к кривой y = g(x) , которая произвольна. Имеем u = x , v = -y . Тогда u’_x = 1, v’_y = - 1 , т.е. условия Коши – Римана ( 20 ) для w = z* не выполняются.

ФКП w = u(x,y) + i v(x,y) , зависящая от двух переменных , всегда является аналитической, если фактически зависит только от их комбинации x + i y , т.е. является функцией одной независимой переменной z . Покажем, что это требование эквивалентно условию Коши – Римана.

Заменим в w(x,y) x на z – iy и продифференцируем по у .

= + i [ ] =

= -i + i [ ] =

При выполнении условий Коши – Римана получаем , т.е. функция w не зависит от у , а только от z . Т.о., замена в функции действительной переменной f(x) аргумента х на КП z приводит к аналитической функции f(z) .

Пр. Функция w = x + 2i y = z + iy не аналитическая, а функция w = x² – y² + 2ixy = z² - аналитическая.

Вычислим производные от нескольких элементарных функций.

1. w = z² . Т.к.u = x² – y², v = 2xy, то = = = 2x + i2y = 2z

Аналогично доказывается общая формула = n z^{n - 1} ( 23 )

2. w = e^z . Т.к. по ( 11 ) e^z = e^x (cos y + i sin y) , то = = e^x cos y + i sin y = e^z

Производная от экспоненты равна самой функции = e^z ( 24 )

3. w = sin z . Т.к. по ( 12 ) sin z = sin x ch y + i cos x sh y , то c учетом ( 13 ) имеем

= = cos x ch y - i sin x sh y = cos z ( 25 )

4. w = ln z . Т.к. по ( 16 ) ln z = ln ( ) + i [ arctg( ) + 2k ] , то

= = + i = = ( 26 )

Аналогично вычисляются следующие производные

( cos z )` = - sin z , ( sh z )` = ch z , ( ch z )` = sh z ,

( arcsin z )` = , (arcos z )` = , ( arctg z )` = ( 27 )

Таким образом, производные от основных элементарных функций от действительных и комплексных переменных полностью совпадают, также как и все правила дифференцирования.

Продифференцируем первое уравнение из ( 21 ) по х , второе по у и сложим их

, ( 28 )

В результате получаем уравнение Лапласа для u и аналогичным образом для v , т.е. мнимая и действительная части всякой аналитической функции являются функциями гармоническими. Их общее свойство: изменение функции вдоль х и вдоль у идет с одинаковым по модулю ускорением. Но не всякое сочетание двух гармонических функций образует аналитическую функцию. Функции u и v должны быть сопряженными. Зная u можно построить v и наоборот.

Пр. Дана действительная часть u(x,y) = x² – y² – x дифференцируемой функции f(z), где z = x + iy. Найти функцию f(z).

Решение. Вычисляем . Т.к. ( 1 условие Коши – Римана), то . Это ДУ интегрируем v(x,y) = 2xy – y + , где - произвольная функция. Это решение дифференцируем по х : = 2y + . Т.к. ( 2 условие Коши – Римана), то = - 2y - . Но из условия задачи следует . Сравнение производных дает = 0 или = const , т.е сопряженная функция равна v(x,y) = 2xy – y + С .

Ответ: f(z) = (x² – y² – x) + i (2xy – y +С) = (x² – y²) +i 2xy + (x + i y) + C = z² + z + C

Конформное отображение.

Дана аналитическая функция w = f(z) , которая сопоставляет точкам области D точки области W. Выберем в D две близко расположенные точки m и m₁ . Им соответствуют точки М и М₁ в W. Отрезки mm₁ и MM₁ соединяют z с z + z и w с w + w . Этим векторам соответствуют КЧ z и w .

Отношение модулей векторов равно . Перейдем к пределу m₁ m

lim = lim = |f `(z)| ( z 0)

т.е. модуль производной показывает во сколько раз длина отрезка в окрестности точки z больше длины отображения этого отрезка.

Пусть m₁ приближается к m вдоль линии l . Тогда соответствующее движение М₁ к М пойдет по линии L . Аргумент КЧ z определяет угол между вектором mm₁ и осью Ох , а аргумент w между вектором ММ₁ и осью Ou. Разность этих аргументов определит угол между векторами mm₁ и ММ₁ , причем, разность аргументов равна аргументу частного

arg w - arg z = arg , ( )

При m₁ m секущие mm₁ и ММ₁ становятся касательными и предел

lim arg = arg f `(z) ( z 0)

о пределит угол между касательной к l в точке z и касательной к L в точке w, т.е. arg f `(z) дает угол поворота прямой в точке z в результате преобразования f(z). Этот угол не зависит от параметров линии. Поэтому, при прохождении через точку z двух линий l и l₁ под углом их отображения L и L₁ будут пересекаться под тем же углом .

Сохранение угла приводит к тому, что бесконечно малый треугольник в окрестности точки z отображается в подобный треугольник в плоскости w, т.е. его стороны изменяют длины в отношении |f `(z)| :1 и поворачиваются на угол arg f `(z) . Это свойство подобия следует из факта существования производной, т.е. аналитичности функции f(z).

Опр. Конформным ( подобным ) отображением наз. отображение с помощью аналитической функции.

Пр. При помощи функции w = z³ отобразить на плоскость uOv линию y = x .

Решение. Имеем w = ( x + iy)³ = x³ + 3x²iy + 3x(iy)² + (iy)³ = (x³ -3xy²) + (3x²y – y³) i , т.е.

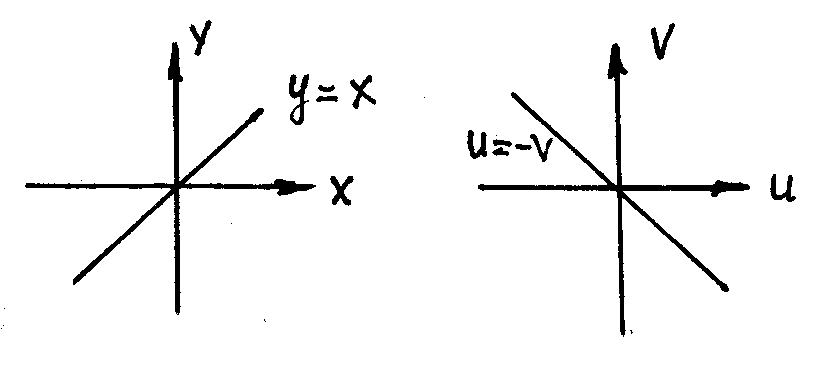
u = x³ - 3xy² , v = 3x²y – y³ . Определим значение этих координат для точек линии y = x : u = - 2x³ , v = 2x³, т.е. v = - u . Это биссектриса 2 и 4 квадранта.

Пр. При помощи функции w = 2z +1 отобразить на плоскость uOv окружность x²+y²=1.

Решение. Имеем w = 2(x + iy) + 1 = (2x + 1) + 2yi , т.е. u = (2x + 1) , v = 2y . Находим обратное преобразование координат x = (u – 1)/2 , y = v/2 и делаем замену переменных в уравнении окружности [(u – 1)/2]² + [v/2]² = 1 (u – 1)² + v² = 4 . Отображение есть окружность с радиусом 2 и центром в точке (1;0).

12 ВОПРОС Теорема Коши.

Если f(z) аналитическая функция в односвязной области D , то интеграл f(z) dz зависит только от положения конечных точек А и В кривой L и не зависит от формы кривой, или интеграл по замкнутой кривой всегда равен нулю.

f(z) dz = 0 ( 34 )

Доказательство. От криволинейного интеграла по замкнутому контуру на плоскости всегда можно перейти к двойному интегралу по области, ограниченной этим контуром по формуле Грина P(x,y) dx + Q(x,y) dy =

В нашем случае

u dx – v dy = - ; v dx + u dy =

но частные производные от аналитической функции f(z) удовлетворяют условиям Коши – Римана , , которые обращают эти интегралы в ноль.

Неопределенный интеграл от ФКП.

Рассмотрим выражение F(z) = f( ) d , где f( ) – аналитическая функция в области D , а точки z₀ и z соединяет произвольная гладкая кривая L . Функция F(z) , удовлетворяет равенству

F`(z) = f(z) ( 35 )

Действительно, при h 0

F`(z) = lim = lim = lim =

= f(z) + lim = f(z)

В ближайшей окрестности точки z функция отличается от f(z) на бесконечно малую (h) более высокого порядка, чем h . Т.к. F(z) имеет производную, то она является аналитической и наз. первообразной для f(z). Её значение зависит от выбора точки z₀ и она определяется с точностью до константы.

Опр. Совокупность всех первообразных ФКП f(z) наз. неопределенным интегралом

f(z) dz = F(z) + C ( 36 )

Правила вычисления интегралов комплексных и действительных переменных совпадают.

Основная теорема интегрального исчисления.

Интеграл от функции f(z) , аналитической в D, равен приращению её первообразной функции, при переходе из начальной в конечную точку пути интегрирования

f(z) dz = F(b) - F(a) ( 37 )

Действительно, интеграл f( ) d = F(z) + C дает первообразную с точностью до константы. Пусть z z₀ и контур замыкается. Тогда по теореме Коши F(z₀) + C = 0 или C = - F(z₀) , т.е. константа равна первообразной в начальной точке.

Вычислим теперь Пр.1 по формуле ( 37 ). f(z) dz = (1 – iz)dz =

= (1 – iz)d(1 – iz) = (1 – iz)² |₁^-i = [ (1 + i²)² – (1 – i)² ] = -1

Пр.2 Вычислить z² dz , если прямая АВ соединяет точки z_А = 1, z_B = i

z² dz = z²dz = 1/3 z³ |₁ⁱ = -1/3 (1 + i )

Формула Коши.

Формула Коши выражает значение аналитической функции в любой точке z внутри области определения через её значения на произвольном контуре, окаймляющем точку.

f(z₀) = ( 38 )

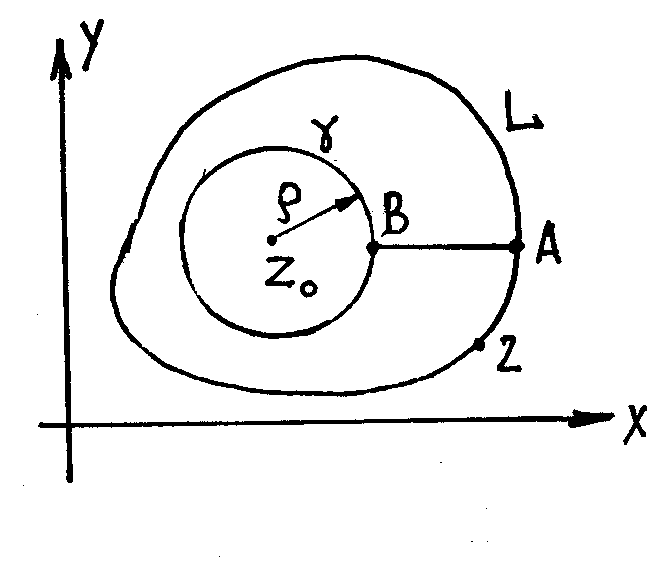
Доказательство. Вокруг выделенной точки z₀ проведем окружность радиуса и соединим её прямой АВ с замкнутым контуром L. Контур L’₊ = AB + _- + BA + L₊ , охватывает кольцевую область, где функция f(z)/(z₀ – z) аналитическая. По теореме Коши ( 34 ) и свойствам ( 31 )

имеем = - - + = 0 , т.е. интеграл по внешнему контуру кольцевой области равен интегралу по внутреннему контуру того же направления

= ( 39 )

Вычислим его. = + = J₁ + J₂

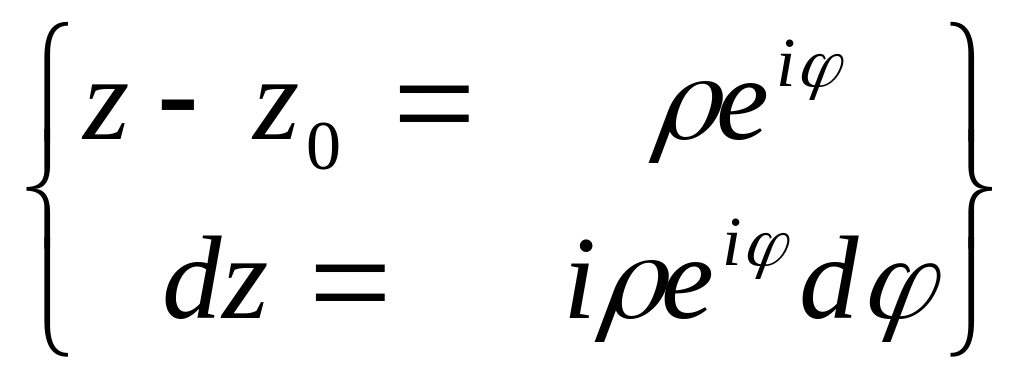J₁ = f(z₀) = = i f(z₀) = 2 i f(z₀)

В J₂ приращение функции заменим на модуль его максимального значения |f(z)– f(z₀)| < , тогда J₂ < | | = 2 . Т.к. радиус произволен, то при 0 и 0, т.е. J₂ = 0. Отсюда следует формула ( 38 ), которая дает явный вид зависимости функции от z₀ . Продифференцируем ( 38 ) по z₀ n раз и получим

f⁽ⁿ⁾(z₀) =