
- •3.2 Центральная предельная теорема и ее применения.
- •3.3. Предельные теоремы в схеме Бернулли.
- •Упражнения
- •Ответы к упражнениям
- •Задание для самостоятельной работы
- •Задание для самостоятельной работы
- •3.4. Дополнительные задачи, связанные с центральной предельной теоремой
- •Контрольные вопросы к главе 3
Задание для самостоятельной работы
Решить задачи: [1], гл.18, №№ 556, 557, 559, 561, 562, 563, 565, 566, 567, 569, 570.
Нормальная асимптотика закона Пуассона.
Теорема 3.3.3.
Пусть
![]() ,
,
![]() - стандартизованная пуассоновская
случайная величина. Тогда для
характеристической функции
- стандартизованная пуассоновская
случайная величина. Тогда для
характеристической функции
![]() справедливо утверждение:
справедливо утверждение:
![]() .
На основании свойства 6) характеристической
функции это означает, что предельным
законом для
.
На основании свойства 6) характеристической
функции это означает, что предельным
законом для
![]() при
при
![]() является нормальный
.
является нормальный
.
◄ Доказательство см. [1], задача 18.572►
Из утверждения
теоремы следует, что при достаточно
больших значениях параметра
![]() можно приближенно аппроксимировать
пуассоновское распределение нормальным.
можно приближенно аппроксимировать
пуассоновское распределение нормальным.
Пример 3.3.17.
Для некоторого автопарка среднее число
автобусов
,
отправляемых в ремонт после месяца
эксплуатации на городских линиях, равно
4. Считая, что
подчиняется закону Пуассона с параметром
=4,
вычислить вероятности событий
![]() для
для
![]() двумя способами: по точной формуле для
пуассоновского распределения и в
приближении нормальности.
двумя способами: по точной формуле для
пуассоновского распределения и в
приближении нормальности.
◄ Обозначим
![]() - точное значение искомой вероятности
(находим по таблице П4 задачника []);
- точное значение искомой вероятности
(находим по таблице П4 задачника []);
![]() - в приближении
нормальности. Результаты вычислений
представлены в таблице 3.3.3, где указаны
относительные погрешности вычислений
по приближенной формуле.
- в приближении
нормальности. Результаты вычислений
представлены в таблице 3.3.3, где указаны
относительные погрешности вычислений
по приближенной формуле.
Таблица 3.3.3.
m |
|
|
|
1 |
0,98168 |
0,9332 |
4,94 |
2 |
0,7619 |
0,8413 |
10,42 |
4 |
0,56653 |
0,5 |
11,7 |
6 |
0,21487 |
0,1587 |
26 |
Снова наблюдается
картина, аналогичная той, которая
получается при аппроксимации биномиального
распределения нормальным (см.табл.3.3.2):
точность приближения резко падает при
удалении левой границы промежутка
от среднего значения
![]() .
Заметим однако, что значение
=4
не является достаточно большим, чтобы
гарантировать хорошую точность
нормального приближения ►
.
Заметим однако, что значение
=4
не является достаточно большим, чтобы
гарантировать хорошую точность
нормального приближения ►
Пример 3.3.18.
Обследуются две группы деловых людей.
В первой группе (экологи) имеется в
среднем 1% курящих. Во второй (политики)
– число курящих составляет в среднем
10%. Обозначим
![]() - число курящих для каждой группы.
Вычислить
- число курящих для каждой группы.
Вычислить
![]() .
.
◄ Очевидно можно
считать, что
![]() ,
где
,
где
![]() =0,01;
=0,01;
![]() =0,1.
Таким образом, для первой группы
выполняются условия:
=0,1.
Таким образом, для первой группы
выполняются условия:
![]() ,
,
![]() 1
и
1
и
![]() =2=
=2=![]() ,
то есть выполнены условия применимости
теоремы Пуассона (закон редких явлений).
Используя пуассоновскую аппроксимацию
биномиального распределения, получаем:
,
то есть выполнены условия применимости
теоремы Пуассона (закон редких явлений).
Используя пуассоновскую аппроксимацию
биномиального распределения, получаем:
![]() =0,00003.
=0,00003.
Для второй группы
выполняются условия:
![]() =20,
=20,
![]() =
=![]() =4,24>1
и промежуток
=4,24>1
и промежуток
![]() содержит среднее значение. Следовательно
можно ожидать, что применение интегральной
теоремы Муавра-Лапласа даст приемлемую
точность. Имеем:
содержит среднее значение. Следовательно
можно ожидать, что применение интегральной
теоремы Муавра-Лапласа даст приемлемую
точность. Имеем:
 =0,9909.
=0,9909.
Заметим, что если
для второй группы принять за основу не
биномиальное, а пуассоновское распределение
с
![]() =20
1,
то применяя нормальную аппроксимацию
непосредственно к пуассоновскому
распределению (теорема 3.3.3), получим:
=20
1,
то применяя нормальную аппроксимацию
непосредственно к пуассоновскому
распределению (теорема 3.3.3), получим:
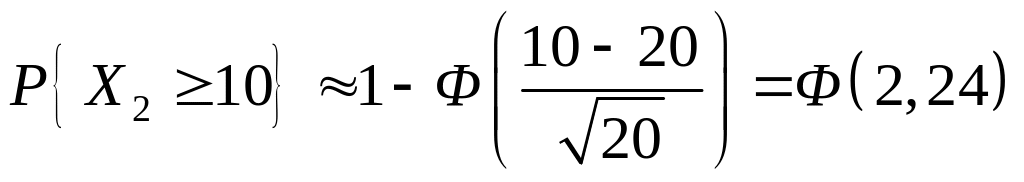 =0,9873.
Заметим, что относительная погрешность
данного результата по сравнению с
предыдущим составляет 0,34%.►
=0,9873.
Заметим, что относительная погрешность
данного результата по сравнению с
предыдущим составляет 0,34%.►
