Раздел 9 Задача линейного программирования с ограничениями целочисленности
Во всех рассмотренных выше задачах линейного программирования мы предполагали, что все переменные принимают вещественные значения. Например, в задаче об оптимальном плане производства предполагалось, что завод производит некоторые бесконечно делимые виды продукции, например, цемент или стиральный порошок. Представим теперь, что наш завод производит разнообразные виды инструментов: дрели, пилы, молотки и т.п. Разумеется, теперь план производства должен выражаться целыми числами. (Мы не можем планировать произвести 132.35 дрелей.) Мы имеет дополнительное ограничение целочисленности. Как решать такие задачи линейного программирования? Рассмотрим для простоты задачу типа (2.1)-(2.2) о выборе наилучшего плана производства.
Способ 1, округление. Если решения, близкие к оптимальным, выражаются достаточно большими целыми числами, мы можем сначала решить задачу линейного программирования без ограничения целочисленности; получить её оптимальное решение, выражающееся, вообще говоря, вещественными числами; а затем, округлить все компоненты оптимального решения до целых чисел. Например, если оптимальное решение – это набор (348.2, 236.7, 138.9, 429.5), то решение (348, 236, 138, 429) будет либо оптимальным для целочисленной задачи, либо не очень отличающимся от этого оптимального (кроме некоторых особо исключительных ситуаций). Такое отклонение не очень существенно, если мы имеем дело с большими целочисленными значениями.
В случае, когда значения не очень велики, нам необходимы точные методы.
Способ 2, методы отсечения. Сначала, как и выше, мы решаем нашу задачу без ограничения целочисленности рассмотренными ранее методами. Если получившееся оптимальное решение целочисленное, то оно, очевидно, является искомым и задача решена. В противном случае мы добавляем к первоначальному набору ограничений новое ограничение, которое должно обладать следующими тремя свойствами:
ограничение – линейное;
должно отсекать найденное нецелочисленное решение (т.е. это решение не должно ему удовлетворять);
не должно отсекать ни одного целочисленного допустимого решения.
Такое ограничение называется правильным отсечением. Далее решается новая задача с добавленным правильным отсечением и всё рассуждение повторяется – вплоть до получения искомого целочисленного плана, решения исходной задачи.
Рассмотрим один из способов построения
правильного отсечения, разработанный
Гомори. Рассмотрим для примера некоторую
задачу линейного программирования
(без ограничения целочисленности),
имеющую конечное оптимальное решение;
и пусть на последнем шаге симплекс-метода
мы получили следующие выражения базисных
переменных, к примеру,
через свободные переменные
:
(9.1)
Таким образом, оптимальным решением
задачи без ограничений целочисленности
является соответствующее данному шагу
базисное решение
.
Если данный вектор целочисленный, то и
целочисленная задача решена: он является
её решением. В противном случае, пусть,
скажем, число
− нецелое. Тогда Гомори предлагает
рассмотреть ограничение
.
(9.2)
(Здесь фигурными скобками обозначена,
как обычно, дробная часть числа: например,
.)
Установим, что оно является правильным
отсечением:
Его линейность очевидна.
При подстановке в (9.2) значений оптимального нецелочисленного решения получаем
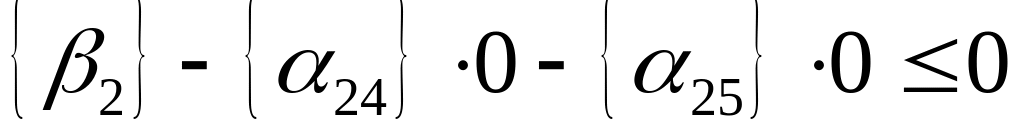или
,
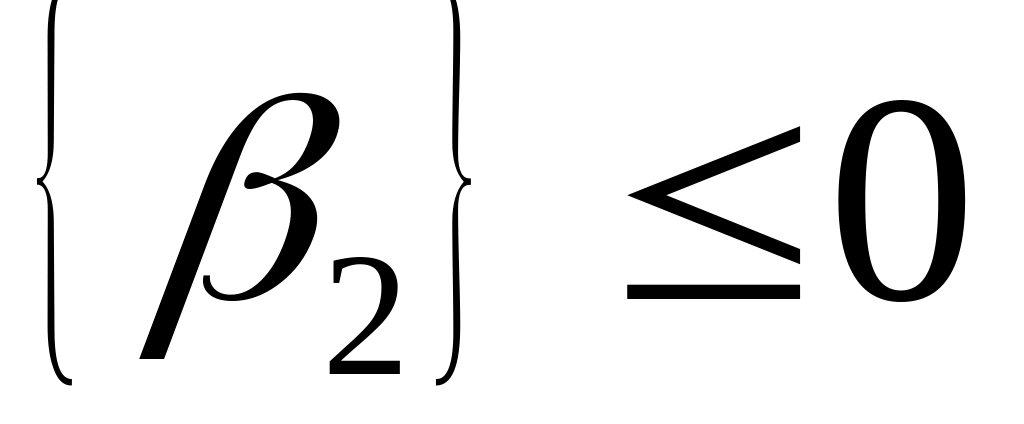что неверно, т.к.
− нецелое.
Пусть ( , ) – допустимое целочисленное решение. Тогда оно удовлетворяет (9.2) и, в частности, второму уравнению, в силу которого имеем
.
Отсюда в силу простых свойств дробной
части (она не изменяется при прибавлении
целого числа и имеет место неравенство
для любых вещественных чисел
)
выводим искомое неравенство
(в силу того, что числа
− неотрицательные целые и следующего
следствия указанного выше неравенства:
для любых вещественных
и любых целых неотрицательных
).
Итак, ограничение (9.2) – правильное отсечение. Мы добавляем его к ограничениям задачи и решаем новую задачу линейного программирования, и затем всё повторяется до тех пор, пока мы не получим в качестве оптимального целочисленное решение, которое и будет искомым для первоначальной целочисленной задачи.