Варианты заданий:
1 вариант |
|
2 вариант |
|
3 вариант |
|
4 вариант |
|
5 вариант |
|
6 вариант |
|
7 вариант |
|
8 вариант |
|
9 вариант |
|
10 вариант |
|
11 вариант |
|
12 вариант |
|
13 вариант |
,
|
14 вариант |
|
15 вариант |
|
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
.
,
,
,
,
.
,
,
,
,
.
Задача
3:
Определить равновесный размер популяции,
если на
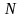особей
в единицу времени,
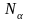особей
рождается, а гибнет
.
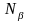Предполагается при этом, что начальная
численность популяции равна
особям.
Построить график логистической кривой.
Решение:
Определим
величины
,
,
,
,
.
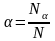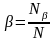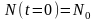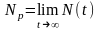Тогда согласно модели Мальтуса
,
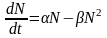найдем соответствующие составляющие,
при этом разделим переменные и
проинтегрируем:
.
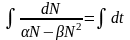Работаем с правой частью последнего равенства:
.
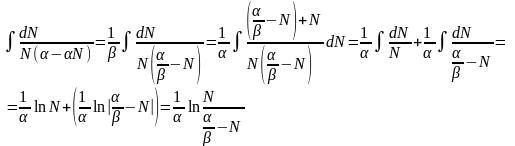Подставляя
в последнее равенство:
,
,
,
.
,
.
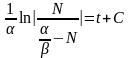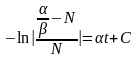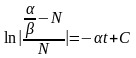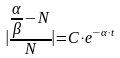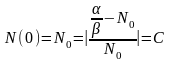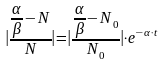Чтобы
не путать с рождаемостью, обозначим
параметр
,
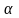стоящий под степенью экспоненты как
,
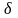являющийся характеристикой
пропорциональности роста численности
популяции. Для его нахождения, используем
тот же подход, что и в задаче 1.
а)
если
,
,
.
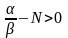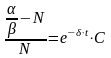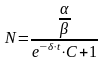б)
если
,
,
.
.
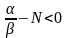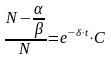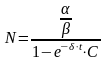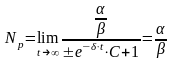, поэтому используем формулу .
Варианты заданий:
1 вариант |
|
2 вариант |
|
3 вариант |
,
|
4 вариант |
|
5 вариант |
,
|
6 вариант |
|
7 вариант |
|
8 вариант |
,
|
9 вариант |
|
10 вариант |
,
,
|
11 вариант |
|
12 вариант |
|
13 вариант |
|
14 вариант |
|
15 вариант |
|
,
,
,
,
.
,
,
,
,
.
,
,
,
.
,
,
,
,
.
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
.
,
,
,
,
.
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
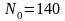
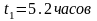
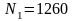
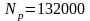
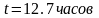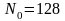
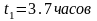
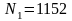
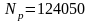
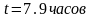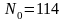
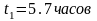
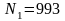
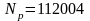
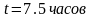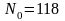
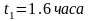
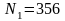
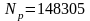
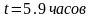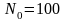
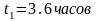
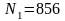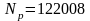
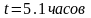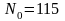
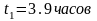
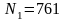
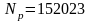
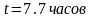
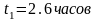
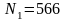
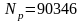
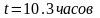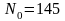
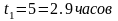
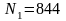
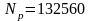
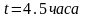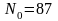
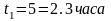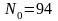
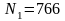
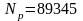
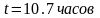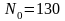
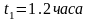
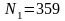
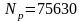
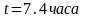
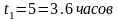
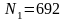
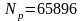
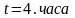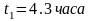
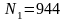
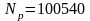
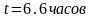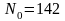
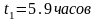
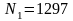
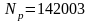
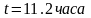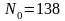
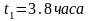
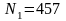
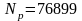
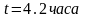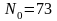
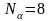
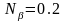
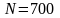
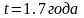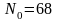
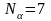
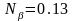
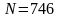
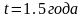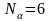
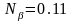
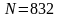
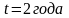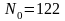
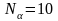
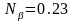
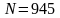
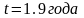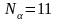
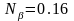
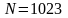
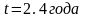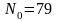
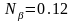
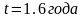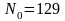
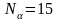
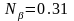
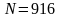
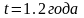
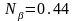
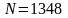
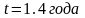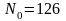
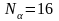
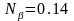
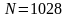
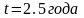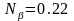
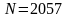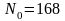
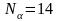
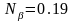
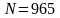
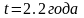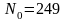
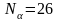
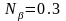
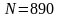
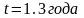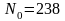
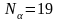
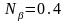
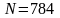
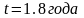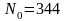
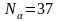
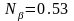
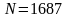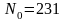
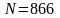
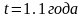