
- •Лабораторные работы по мат. Моделированию (заочники) Лабораторная работа №1.
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Лабораторная работа №2.
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Лабораторная работа №3.
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Лабораторная работа №4.
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Варианты заданий:
- •Лабораторная работа №5.
- •Варианты заданий:
- •Варианты заданий:
Лабораторные работы по мат. Моделированию (заочники) Лабораторная работа №1.
Цель: расчет задач по теме «Гидростатика и гидродинамика»
Задача
1.
Из отверстия в дне высокого сосуда
вытекает вода. Сечение сосуда
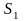 ,
сечение струи
,
сечение струи
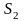 (рис. 2). Найдите ускорение, с которым
перемещается уровень воды в сосуде.
(рис. 2). Найдите ускорение, с которым
перемещается уровень воды в сосуде.
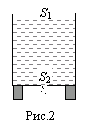
Решение: Будем считать жидкость несжимаемой. Тогда для каждого момента времени, согласно уравнению неразрывности струи, можно записать
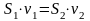 ,
(1.1)
,
(1.1)
где
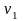 - скорость воды в сосуде,
- скорость воды в сосуде,
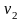 - скорость воды в струе вблизи отверстия.
Возьмем производную по времени от (1.1)
- скорость воды в струе вблизи отверстия.
Возьмем производную по времени от (1.1)
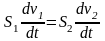 ,
,
где
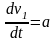 - ускорение воды в сосуде,
- ускорение воды в сосуде,
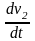 - ускорение свободного падения, так на
выходе из сосуда вода начинает свободно
падать. Таким образом,
- ускорение свободного падения, так на
выходе из сосуда вода начинает свободно
падать. Таким образом,
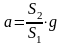 .
.
Варианты заданий:
1 вариант |
S1=2.3 см2, S2=0.3 см2.
|
2 вариант |
S1=2.4 см2, S2=0.2 см2.
|
3 вариант |
S1=2.7 см2, S2=0.3 см2.
|
4 вариант |
S1=2.3 см2, S2=0.8 см2.
|
5 вариант |
S1=2.3 см2, S2=0.3 см2.
|
6 вариант |
S1=2.8 см2, S2=0.7 см2.
|
7 вариант |
S1=2.5 см2, S2=0.4 см2.
|
8 вариант |
S1=2.9 см2, S2=0.25 см2.
|
9 вариант |
S1=2.45 см2, S2=0.33 см2.
|
10 вариант |
S1=2.43 см2, S2=0.32 см2.
|
11 вариант |
S1=2.56 см2, S2=0.36 см2.
|
12 вариант |
S1=2.49 см2, S2=0.23 см2.
|
13 вариант |
S1=2.38 см2, S2=0.25 см2.
|
14 вариант |
S1=2.54 см2, S2=0.31 см2.
|
15 вариант |
S1=2.46 см2, S2=0.32 см2.
|
Задача
2.
И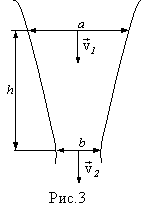 з
крана выливается вода. Начиная с
некоторого места, диаметр струи
уменьшается на протяжении
з
крана выливается вода. Начиная с
некоторого места, диаметр струи
уменьшается на протяжении
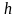 от
от
 до
до
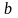 (рис. 3). Сколько воды вытечет из крана
за время
(рис. 3). Сколько воды вытечет из крана
за время
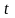 .
.
Решение: Воспользуемся условием стационарности течения несжимаемой жидкости
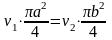 .
(1.2)
.
(1.2)
Для идеальной жидкости справедливо уравнение Бернулли:
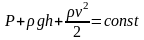 .
.
Поскольку жидкость свободно падает, то давления в обоих сечениях одинаковы, и уравнение Бернулли принимает вид:
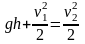 .
(1.3)
.
(1.3)
За время через любое сечение протекает один и тот же объем воды, поэтому можно записать
 .
(1.4)
.
(1.4)
Выразим скорость из (1.2) и (1.3):
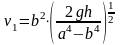 .
.
Подставим полученное значение в (1.4) и получим окончательный ответ:
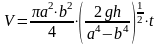 .
.
