Раздел 2. Дифференциальное исчисление функции одной переменной.

1.Производная. Таблица производных.

От руки написать.

2.Общее правило дифференцирования.

Правила дифференцирования

Теорема. Если функции u=f(x), v=g(x) дифференцируемы в точке х0, то сумма, разность, произведение и частное этих функций также дифференцируемы в точке ч0 и выполняются следующие формулы:

(U+(-)v)?=u’+(-)v’

(uv)’= u’v + uv’

(u/v)’= (u’v - uv’)/v2

Правило дифференцирования сложной функции.

Производная сложной и обратной функций.

Теорема. Если функция y=f(x) дифференцируема в точке t0, g(t0)=x0, то сложная функция y=f(g(x)) также дифференцируема в точке t0 и выполняется след. Формула:

f’(g(x))=f’(x0)*g’(t0)

Теорема. Если y=f(x) имеет обратную ф-ю x=g(y) и в точке х0 производная f?(x) не равна 0, то обратная функция g(y) диф-ма в точке y0=f(x0) и

g’(y)=1/f(x0)

Правило логарифмического дифференцирования.

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него.

Производная параметрически заданной функции

Если функция f задана параметрически x = φ(t), y = ψ(t), α < t < β, где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то

5Производная сложной и обратной функций.

Теорема. Если функция y=f(x) дифференцируема в точке t0, g(t0)=x0, то сложная функция y=f(g(x)) также дифференцируема в точке t0 и выполняется след. Формула:

f’(g(x))=f’(x0)*g’(t0)

Теорема. Если y=f(x) имеет обратную ф-ю x=g(y) и в точке х0 производная f?(x) не равна 0, то обратная функция g(y) диф-ма в точке y0=f(x0) и

g’(y)=1/f(x0)

Производная элементарных функций.

Обл. определения производной f’(x) явл. множество всех точек x0, в которых y=f(x) имеет конечную производную.

Производная каждой элементарной ф-и явл. элементарной ф-ей.

Производная логарифмической ф-и: (logax)’=1/xlna

Производная показательной ф-и: ax= ax lna

Производная степенной ф-и: (xa)’ = axa-1

Производная тригонометрической функции:

(Sinx)’=cosx

(cosx)’=-sinx

(tgx)’=1/cos2x

Производные обратных тригонометрических функций:

(Arcsinx)’=1/(1-x2)1/2

(Arccosx)’=-1/(1-x2)1/2

(arctgx)’=1/(1+ x2)

6.Дифференциал.

Дифференциал (от лат. differentia — разность, различие) - в математике, главная линейная часть приращения функции. Если функция y = f (x) одного переменного х имеет при х = х0 производную, то приращение Δy = f (x0 + Δx) - f (x0) функции f (x) можно представить в виде Δy = f' (x0) Δx + R, где член R бесконечно мал по сравнению с Δх. Первый член dy = f' (x0) Δх в этом разложении и называется дифференциалом функции f (x) в точке x0. Из этой формулы видно, что дифференциал dy линейно зависит от приращения независимого переменного Δx, а равенство Δy = dy + R показывает, в каком смысле Д. dy является главной частью приращения Δy.

7.Теорема Ферма.

Если функция у = f (х),  определенная в интервале (а ; b), достигает в  некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует  производная f ′(с), то f ′(с) = 0.  

Геометрический смысл этой теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой с параллельна оси абсцисс.

8.Теорема Ролля.

Если функция у = f (х),  непрерывная на отрезке [а ; b] и  дифференцируемая в интервале (а ; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а ; b) существует такая точка с, что f ′(с) = 0. Геометрически эта теорема означает  следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс.

9.Теорема Коши.

Если функции f (х) и g (х): 1) непрерывны на отрезке [а ; b];  

2)  дифференцируемы в интервале (а ; b);  

3) g'(x) ≠ 0 в этом  интервале,  

то в интервале (а ; b) существует  такая точка с, что имеет место равенство 

 

10.Теорема Лагранжа.

Если функция у = f (х) непрерывна на отрезке [а ; b] и  дифференцируема в интервале (а ; b), то в этом интервале найдется такая точка с, что  

Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х)  между точками А и В найдется такая внутренняя точка С, что касательная к графику в точке С параллельна хорде АВ.

11. Правило Лапиталя.

Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

lim(g) не равна нулю в окрестности а

lim(g) = lim(f) = 0 или бесконечности

функции диффиренцируемы в окрестности а

12. Формула Маклорена для функций : sinx, cosx, e^x.

Формулы Маклорена некоторых элементарных функций

1) f(x)=e^x ->'(x)=f "(x)=…=f(n+1)(x)=e^x ->0)=f '(0)=f "(0)=…=f(n+1)(0)=1

2) f(x)=sinx

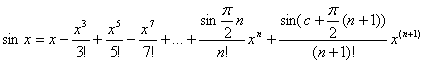(6)

3) f(x)=cosx

(7)

13 . Необходимый и достаточный признаки монотонности функции.

Связь между непрерывностью и дифференцируемостью функции. Если функция  f ( x ) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно:  непрерывная функция может не иметь производной.  

С л е д с т в и е . Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.

Достаточные признаки монотонности функции.

Если  f ’( x ) > 0  в каждой точке интервала ( a, b ), то функция  f ( x ) возрастает на этом интервале.

Если  f ’( x ) < 0  в каждой точке интервала ( a, b ) , то функция  f ( x ) убывает на этом интервале.

13. Необходимый и достаточный признаки существования экстремума.

Необходимое условие экстремума. Если x0 - точка экстремума функции f ( x )  и производная  f’  существует в этой точке, то  f’ ( x0 ) = 0.

Эта теорема - необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке.

Достаточные условия экстремума.

Если производная при переходе через точку  x0  меняет свой знак с плюса на минус, то  x0  - точка максимума.

Если производная при переходе через точку  x0  меняет свой знак с минуса на плюс, то  x0  - точка минимума.

 

15.Достаточное условие выпуклости.

Если вторая производная дважды дифференцируемой функции положительна (отрицательна) на множестве X, то функция выпукла вниз (вверх) на этом множестве. Необходимое условие выпуклости слабее: если функция выпукла вниз (вверх) на множестве X, то f''(x)і 0, xО X (или f''(x)Ј 0 ) xО X. Например, функция y = x4 выпукла вниз на всей числовой прямой, но y'' = 12x2 обращается в ноль при x = 0.

16. Необходимое и достаточное условие существование тчк перегиба.

Необходимое условие существования точки перегиба: если функция f(x), дважды дифференцируемая в некоторой окрестности точки x0, имеет в x0 точку перегиба, то .

Достаточное условие существования точки перегиба: если функция f(x) в некоторой окрестности точки x k раз непрерывно дифференцируема, причем k нечётно и , и при , а , то функция f(x) имеет в x0 точку перегиба

17. Необходимое и достаточное условие существование наклонной асимптоты.

Для того чтобы график функции   имел при  наклонную асимптоту, необходимо и достаточно, чтобы существовали два предела

 и 

(   и  )