15.Дифракция света. Условия наблюдения дифракции. Принцип Гюйгенса. Принцип Гюйгенса-Френеля.

ДИФРАКЦИЯ СВЕТА

в узком смысле — явление огибания лучами света контура непрозрачных тел и, следовательно, проникновение света в область геом. тени; в широком смысле — проявление волновых св-в света в условиях, близких к условиям применимости представлении геометрической оптики.

В естеств. условиях Д. с. обычно наблюдается в виде нерезкой, размытой границы тени предмета, освещаемого удалённым источником. Наиболее контрастна Д. с. в пространств. областях, где плотность потока лучей претерпевает резкое изменение (в области каустической поверхности, фокуса, границы геом. тени и др.). В лабораторных условиях можно выявить структуру света в этих областях, проявляющуюся в чередовании светлых и тёмных (или окрашенных) областей на экране. Иногда эта структура проста, как, напр., при Д. с. на дифракционной решётке, часто очень сложна, напр. в области фокуса линзы. Д. с. на телах с резкими границами используется в инструментальной оптике и, в частности, определяет предел возможностей оптич. устройств.

Принцип Гюйгенса.

каждая точка волновой поверхности является источником вторичных сферических волн

Принцип Гюйгенса-Френеля.

каждая точка волновой поверхности является источником вторичных сферических волн,

которые интерферируют между собой

Условия наблюдения дифракции

-Дифракция происходит на предметах любых размеров, а не только соизмеримых с длиной волны l

Трудности наблюдения заключаются в том, что вследствие малости длины световой волны интерференционные максимумы располагаются очень близко друг к другу, а их интенсивность быстро убывает

16. Законы Френеля. Радиус зоны Френеля для сферической волны и плоской волны.

Законы Френеля

- Для того чтобы найти амплитуду световой волны от точечного монохроматического источника света А в произвольной точке О изотропной среды, надо источник света окружить сферой радиусом r=ct

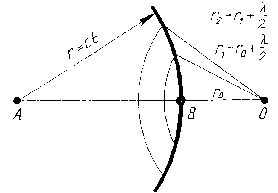
-Интерференция волны от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке P, т. е. необходимо произвести сложение когерентных колебаний от всех вторичных источников на волновой поверхности

-Так как расстояния от них до точки О различны, то колебания будут приходить в различных фазах.

Наименьшее расстояние от точки О до волновой поверхности В равно r0

-Первая зона Френеля ограничивается точками волновой поверхности, расстояния от которых до точки О равны:

где l — длина световой волны

- Вторая зона:

Аналогично определяются границы других зон

17. Дифракция Френеля на круглом отверстии и круглом диске.

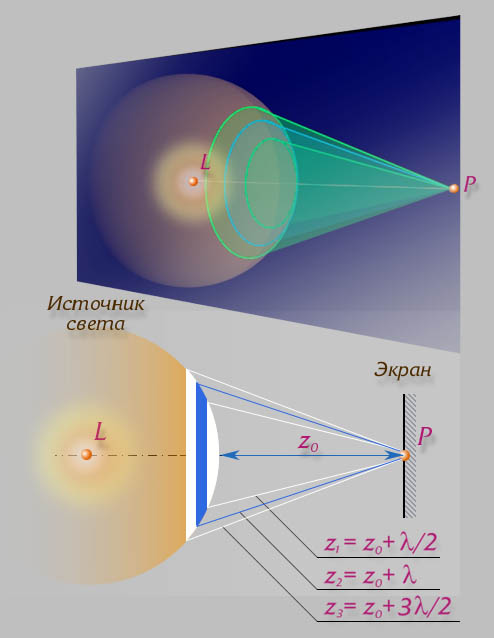
Рассмотрим дифракцию в сходящихся лучах, или дифракцию Френеля, осуществляемую в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию.

Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 1).

Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами,

где знак плюс соответствует нечетным m и минус - четным m.

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А =А1, т.е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием (см. § 177). Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если т нечетное - то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.

Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.

Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то Am ≪ A1 и результирующая амплитуда A = A1/2, т. е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблюдается, свет распространяется, как и в отсутствие круглого отверстия, прямолинейно.

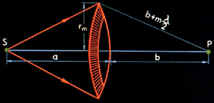
Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем иа экране Э в точке В, лежащей на линии, соединяющей S с центром диска.

В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает т первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна

Или

так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.

С увеличением радиуса диска первая открытая зона Френеля удаляется от точки В и увеличивается угол jт (см. рис.) между нормалью к поверхности этой зоны и направлением на точку В. В результате интенсивность центрального максимума с увеличением размеров диска уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место весьма слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распространяющимся прямолинейно.

Отметим, что дифракция на круглом отверстии и дифракция на диске впервые рассмотрены Френелем.