1.3 Возведение комплексного числа в целую степень и извлечение корня из комплексных чисел

Произведение комплексных чисел, записанных в тригонометрической форме, находится по формуле

(12)

– при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Деление выполняется по формуле

. (13)

Возведение комплексного числа в натуральную степень производится по формуле

. (14)

Следствием формулы (14) является формула Муавра (1667-1754)

. (15)

Извлечение корня n-ой степени из комплексного числа производится по формуле:

(16)

где – корень - ой степени из комплексного числа имеет (только) различных значений. Точки, соответствующие значениям , являются вершинами правильного -угольника, вписанного в окружность радиуса с центром в начале координат. Для геометрического определения корней (16) следует найти по данной формуле одно значение корня, поставить соответствующую точку на окружности, разбить затем окружность на равных частей – таким образом могут быть построены остальные вершины -угольника.

Приведем несколько примеров.

Пример 1. Вычислить ; решение записать в алгебраической, тригонометрической и показательной формах.

Представим число в тригонометрической форме:

.

По формуле(4) находим:

.

Так как здесь , то последняя запись представляет исходное число в тригонометрической форме. В алгебраической форме записи число имеет вид: и в показательной: .

Пример 2. Вычислить .

Представим число в тригонометрической форме: .

По формуле (16) находим:

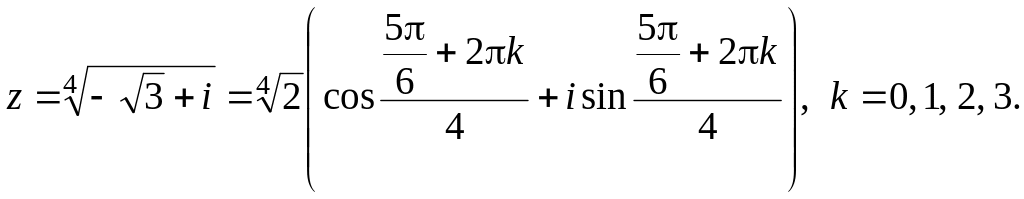
Полагая последовательно равным 0, 1, 2 и 3, находим корни:

; ;

; .

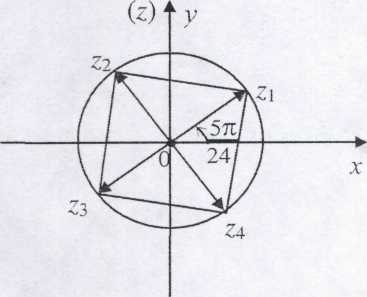
Рисунок 5

Для построения этих чисел на комплексной плоскости проведем окружность радиуса . На окружности отметим точку . Разбивая далее окружность на четыре равные части, изобразим остальные точки (рисунок 5; заметим, что радиан соответствует угол равный 37°30').

Пример 3. Решить уравнение .

Имеем .

Значение определим алгебраическим путем. Положим: ( и – действительные числа). Возводя в квадрат и используя определение равенства комплексных чисел, находим систему уравнений: , , . Исключая , приходим к уравнению , или _. Определим корни уравнения:

.

Знак минус перед корнем следует отбросить, так как – действительное число. Далее находим: и .

Запишем найденные решения: и и, окончательно,

; .

Замечание. Решение квадратных уравнений (иногда) можно найти с помощью теоремы Виета. Пусть требуется решить уравнение . Если взять и , то получим, что , . На основании теоремы Виета устанавливаем, что 1 и – корни исходного уравнения.

1.4 Множества точек на комплексной плоскости. Задание геометрических мест

Приведем некоторые примеры использования геометрического смысла модуля комплексного числа, его аргумента, введенных алгебраических операций.

Пример 1. Какое множество точек на плоскости определяется условием ?

Имеем и, значит, . По условию или . Последнее неравенство определяет множество точек в первом и третьем квадрантах, соответственно над и под гиперболой (рисунок 6).

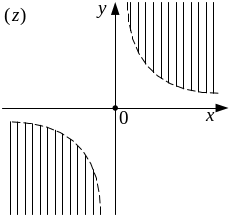
Рисунок 6

Пример 2. Какое множество точек на плоскости определяется условием ?

Комплексное число изображается вектором, началом которого является точка и концом – точка . Угол между этим вектором и осью есть и он меняется в пределах от до . Следовательно, данное неравенство определяет угол между прямыми, выходящими из точки и образующими с осью углы в и (рисунок 7).

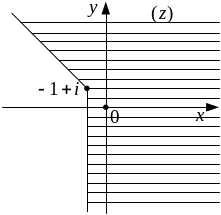
Рисунок 7

Пример 3. Какая кривая задается уравнением , где и – действительные положительные числа, причем .

Модуль есть расстояние между точками и , модуль – расстояние между точками и . По условию сумма расстояний от точки до двух данных точек и есть величина постоянная. Значит, точка лежит на эллипсе. Уравнение этого эллипса имеет вид , где (рисунок 8).

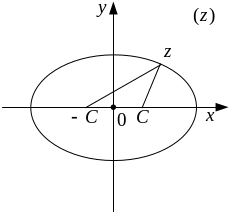
Рисунок 8

Пример 4. Какая кривая определяется уравнением ?

Имеем 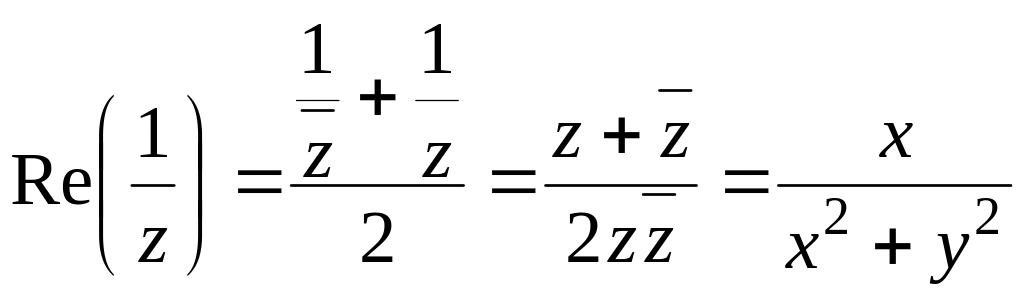. По условию или – это окружность (см. рисунок 9).

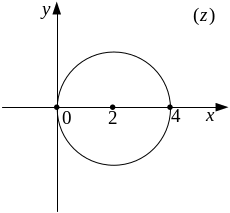
Рисунок 9

Пример 5. Написать в комплексной форме уравнение прямой .

Подставляя и по формуле (9) в уравнение прямой, получаем , или . Обозначив , получим уравнение: – уравнение прямой в комплексной форме.