3 Аналитические функции. Условия Коши-Римана

3.1 Дифференцирование функции комплексного переменного. Аналитичность функции

Определение 1. Функция называется дифференцируемой в точке , если существует предел

. (44)

Этот предел называется производной функции в точке .

Для производной функции комплексного переменного вводятся обозначения , .

Определение 2. Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке.

Теорема 1. Если функция дифференцируема в точке, то она в этой точке непрерывна.

Теорема, обратная данной, неверна, так как можно привести примеры функций, непрерывных в точке, но не являющихся в ней дифференцируемыми.

Теорема 2. Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно, чтобы приращение функции можно было представить в виде: , где .

Теорема 3. Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно, чтобы функции , были дифференцируемы в этой точке и выполнялись условия Коши-Римана (иногда их называют условиями Даламбера-Эйлера):

. (45)

Определение 3. Функция называется аналитической (регулярной) в данной точке , если она дифференцируема как в самой точке , так и в некоторой ее окрестности.

Определение 4. Функция называется аналитической в области , если она аналитична в каждой точке этой области.

Очевидно, что функция, аналитическая в точке, будет и дифференцируема в ней. Обратное может не иметь места.

Из определения следует, что функция аналитична в области , если она дифференцируема в этой области.

Замечание. Так как все определения аналогичны определениям в случае функции действительной переменной, значит для функции комплексной переменной справедливы обычные правила дифференцирования и теоремы о производной сложной и обратной функций.

Для любой аналитической функции имеем

. (46)

Пример 1. Показать, что функция аналитична, и найти .

Получаем , т.е. , . Поэтому , , , и, следовательно, условия (45) выполняются во всей плоскости; по первой из формул (46) имеем .

Пример 2. Является ли функция аналитической хотя бы в одной точке?

Получаем , так что , . Условия Коши–Римана имеют вид: , и выполняются только в точке . Следовательно, функция дифференцируема только в точке и нигде не аналитична. По определению (44) запишем: 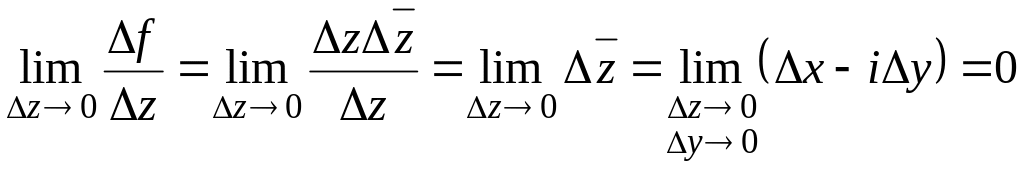. Таким образом, производная существует и равна нулю.

3.2 Гармонические функции. Сопряженно-гармонические функции. Восстановление аналитической функции

Определение 1. Функция называется гармонической в области , если она имеет в этой области непрерывные частные производные до второго порядка включительно и в этой области лапласиан , т.е. .

Определение 2. Две гармонические функции , , удовлетворяющие условию (45), называются сопряженно-гармоническими функциями.

Теорема. Для того чтобы функции , были соответственно действительной и мнимой частями аналитической функции , необходимо и достаточно, чтобы они были сопряженно-гармоническими функциями.

Пользуясь условиями Коши-Римана, аналитическую функцию можно восстановить, если известна ее действительная или мнимая часть .

Пример 1. При каких условиях трехчлен является гармонической функцией?

Находим: , . Лапласиан (т.е. ), если при любом .

Пример 2. Найти аналитическую функцию, если известна ее мнимая часть при дополнительном условии .

Так как , то из условий Коши-Римана (45) находим производные (1); (2). Решив первое из этих уравнений, находим: , где – произвольная функция переменной . Для определения дифференцируем по и подставляем в (2): , откуда и . Следовательно, и окончательно получим:

.

Определим : и ; таким образом, .