3.3 Геометрический смысл модуля и аргумента производной

Если функция аналитична в точке и , то равен коэффициенту растяжения в точке при отображении плоскости на плоскость . Аргумент производной равен углу, на который нужно повернуть касательную в точке к любой гладкой кривой на плоскости , проходящей через точку , чтобы получить направление касательной в точке .

Пример. Найти коэффициент растяжения и угол поворота при отображении в точке .

Имеем , так что . Перейдя от алгебраической формы записи комплексного числа к тригонометрической, получим: , т.е. . угол поворота .

3.4 Конформные отображения

Определение 1. Отображение называется конформным в точке , если оно сохраняет углы между кривыми и обладает свойством постоянства растяжений в точке по всем направлениям, выходящим из точки .

Теорема 1. Если функция аналитическая в точке и , то отображение является конформным в точке .

Определение 2. Функция называется однолистной в области , если для любых из .

Пример 1. Функция не является однолистной на всей комплексной плоскости, так как для и выполняется условие .

Определение 3. Отображение называется конформным в области , если оно конформно в каждой точке области и функция является аналитической и однолистной в области .

Докажем следующую теорему.

Теорема 2. Пусть функция – однолистная и аналитическая в области и в каждой точке области . Тогда отображение будет конформным в области .

Доказательство: в силу условия при и теоремы 1. отображение, осуществляемое функцией , является конформным в каждой точке области D.

Следовательно, отображение будет конформным в области , так как выполняются все условия определения 3.

Таким образом, мы доказали, что условия аналитичности, однолистность и неравенство нулю производной функции является достаточными условиями конформности отображения, осуществляемого этой функцией.

3.5 Основная задача и общие теоремы теории конформных отображений

В настоящем параграфе приведем без доказательства ряд теорем, которые имеют большое значение при решении задач на конформные отображения.

Основной задачей теории конформных отображений является следующая задача.

Даны две области и комплексной плоскости; требуется найти функцию осуществляющую конформное отображение одной из этих областей на другую. Эта задача не всегда имеет решение. Например, невозможно взаимно-однозначное конформное отображение; многосвязной области на односвязную.

Таким образом, возникают вопросы об условиях существования и однозначного определения функции, конформно отображающей область на область .

Б.Риманом в 1851 году была доказана следующая теорема, которую называют основной теоремой теории конформных отображений.

Теорема 3. Пусть и – две произвольные односвязные области, границы которых состоят более чем из одной точки. Тогда существует и только одно конформное отображение области на область такое, что

, , (*)

где , , – заданное действительное число (см. рисунок 13).

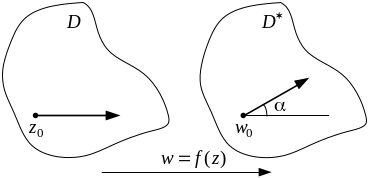
Рисунок 13

Условия (*) называются условиями нормировки конформного отображения. Вместо (*) можно задать другие условия. Например, можно задать

, ,

где , – внутренние, , – граничные точки областей и соответственно, или

, ,

где , , – различные граничные точки области , , , – различные граничные точки области , причем точки , , и , , следуют в порядке положительного обхода границ и областей и соответственно.

Теорема Римана устанавливает факт существования функции, конформно отображающей область на область , но не дает удобного способа построения ее. Кроме того, эта функция выражается через элементарные функции лишь для простых областей. Поэтому изучение частных случаев отображений с помощью комбинаций элементарных функций имеет большое практическое значение.

Приведем без доказательства теорему о соответствии границ.

Теорема 4. Пусть и – односвязные области, причем их границы и – простые замкнутые кусочно-гладкие кривые.

Если функция конформно отображает область на область , то

1) функцию можно непрерывно продолжить на замыкание области , т.е. можно доопределить на так, что получится непрерывная в функция;

2) эта функция отображает однозначно кривую на кривую с сохранением ориентации.

Для практики важен следующий в известном смысле обратный теореме 4. принцип соответствия границ.

Теорема 5. Пусть в односвязной области , ограниченной контуром , задана однозначная аналитическая функция , непрерывная в и осуществляющая взаимно однозначное отображение контура на некоторый контур плоскости . Тогда, если при заданном отображении контуров сохраняется направление обхода, то функция осуществляет конформное отображение области на внутреннюю область , ограниченную контуром .

Из принципа соответствия границ следует, что для того, чтобы определить область , на которую аналитическая функция конформно отображает данную область , достаточно найти контур, на который эта функция отображает границу области и установить направление обхода этого контура.

Пример 1. Найти область , на которую функция конформно отображает область , ограниченную контуром :

.

Решение: пусть , .

Тогда . Отсюда , , т.е. , .

Контур отображается в контур .

или

,

т.е. окружность радиуса 10 с центром в точке .

Легко убедиться, задав контуры параметрическими уравнениями, что положительное направление обхода контура соответствует положительному направлению обхода контура .

Тогда на основании принципа соответствия границ, заключаем, что функция осуществляет конформное отображение внутренности рассматриваемой окружности на внутренность окружности

.

Пример 2. Найти функцию, которая отображает конформно угол плоскости на угол плоскости (рисунок 12).

Решение: поставленную задачу решает комплексная функция , так как она произвольный луч , отображает на луч , . при изменении от 0 до луч описывает открытый угол , а его образ луч описывает открытый угол – верхнюю полуплоскость. Указанное отображение будет однолистным в , аналитичным и , если (точка ).

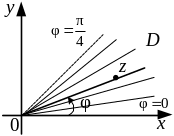
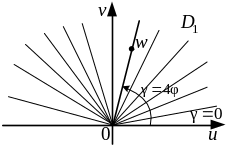
Рисунок 12

12