12. Постановка задачи безусловной оптимизации фнп. Градиентные методы и метод наискорейшего спуска.

ПЗ: àmin. Найти хотя бы один локальный мин.функции , (существует или удовлетворяет определенному условию) с заданной точностью:

1.по решению , где -приблизиженное значение, -лок. Мин.

2.по градиенту ,

К методам 1 –го порядка (градиентным методам).

1)метод наискорейшего спуска

2) градиентный с дробным шагом

3) овражный

В том случае, когда доступна только первая производная, то в качестве направления спуска естественно рассматривать антиградиентное направление. Методы, использующие в качестве направления поиска вектор-градиент, называют градиентными. Алгоритм этих методов отличается от предыдущего отсутствием вычисления вторых производных и добавлением пункта вычисления длины шага.

Метод наискорейшего спуска

Самый известный из семейства градиентных методов это метод наискорейшего спуска. Он так назван потому, что спуск вдоль антиградиентного направления осуществляется в точку минимума.

Алгоритм:

1.вводим x0 (начального приближения), eg-точность по градиенту конечного решения и e1g точность по производной по направлению).

2.Пока /f ’(x0)/<eg, n=0

2.1.вычисляем направление спуска Pk= - f ’(x0)= - grad (x0), при к=к+1

2.2 Производим одномерную оптимизацию поиска из точки х0 вдоль направления Рк, то х1=argmin f(x0+αPk) c точностью e1g (e1g≤eg)

2.3 Критерии останова

Δх=х1-х0, если /Δx/<ex, то аварийный выход, застряли х0, f(x0), f ’(x0), /Δx/-длина последнего шага

2.4х0=х1

3. вывод полученного значения х0, f(x0), f ’(x0)

13. Постановка задачи безусловной оптимизации фнп. Градиентный метод с добрым шагом. Алгоритм выбора длины шага.

ПЗ: àmin. Найти хотя бы один локальный мин.функции , (существует или удовлетворяет определенному условию) с заданной точностью:

1.по решению , где -приблизиженное значение, -лок. Мин.

2.по градиенту ,

Градиентный метод с добрым шагом

Алгоритм этого метода схож с алгоритмом метода наискорейшего спуска кроме п 2.2

Алгоритм:

1.вводим x0 (начального приближения), eg-точность по градиенту конечного решения и e1g точность по производной по направлению).

2.Пока /f ’(x0)/<eg, n=0

2.1.вычисляем направление спуска Pk= - f ’(x0)= - grad (x0), при к=к+1

2.2 Поиск хорошего шага вдоль направления Рк из точки х0 (вместо е1g, будет коэффициент γ дробления шага, коэффициент β, ех также будет меняться)

x=x1+αPk, хороший шаг будет тогда, когда будет выполняться условия существенного убывания

f(x0+αPk)<f(x0)+βα grad (x0)Pk

0.3≤β≤0.7

Поиск хорошего шага осущ-я фиксированием х0, если не выполняется условие существенного убывания с коэ-м α, то делаем простое уменьшение α, α=α*γ, 0.1<α<0.7.

α уменьшаем до тех пор пока функция не будет себя вести как линейная функция.

14. Постановка задачи безусловной оптимизации фнп. Овражный метод.

ПЗ: àmin. Найти хотя бы один локальный мин.функции , (существует или удовлетворяет определенному условию) с заданной точностью:

1.по решению , где -приблизиженное значение, -лок. Мин.

2.по градиенту ,

О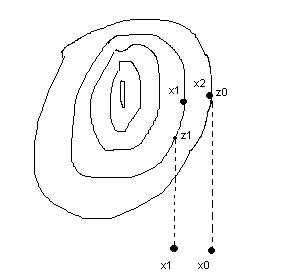 вражный метод

Суть: берется 2 точки х0, х1 и осуществляется спуск Z0 и Z1 и делается шаг. Дальше х2 спускаемся на дно положением Z2. дальше делаем снова шаг и т.д.

Алгоритм:

1. Вводим х0 и х1, коэ – т шага α, точность еg, х ^к=х1

   1. Z0=argmin f(x0+γ (-grad (x0))) c некоторой точностью eg/

   2. Z1=argmin f(x1+β (-grad (x1))), g(x)=f ’(x)=grad (x)

2. Пока не выполняется условие самой лучшей точки, /grad (x^k)/>eg, инициализируем счетчик к=0

2.1 Проводим одномерный поиск Z0 из точки х0 и Z1 из точки х1 .

2.2 переупорядочиваем точки Z1 и Z0, таким образом, чтобы f(Z1)<f(Z0)

2.3 Делаем пробный шаг из точки х2=Z1+α (Z1-Z0)

2.4 Z2=argmin f(x2-γ g (x))

2.5 Анализируем пробный шаг, если шаг удачный f(Z2)<f(Z1), то Z0=Z1, Z1=Z2,

Иначе шаг α= -α/2 и идем к п.2.3- в любом случае

γ- коэффициент шага