1.5 Інженерний розрахунок кожухотрубчастого протиточного теплообмінного апарату на еом з використанням лінійного алгоритму

Крім описаних у лабораторних роботах 1–3 методів моделювання теплообмінних апаратів з побудовою рівнянь теплового балансу для основного потоку і для холодоагента з урахуванням гідродинаміки їх руху, на практиці широко використовують також інженерні методи розрахунку.

Нижче представлений інженерний метод розрахунку кожухотрубчастого протиточного теплообмінника, працюючого в стаціонарному режимі.

При побудові математичної моделі теплообмінника прийняті наступні допущення:

• теплопередача не супроводжується зміною агрегатного стану теплоносіїв;

• втрати теплоти не враховуються;

• коефіцієнти теплопередачі в трубному і міжтрубному просторах розраховуються при початкових температурах теплоносіїв;

• теплоносій, що віддає теплоту («гарячий» поток), направляється у труби, а теплоносій, що сприймає теплоту («холодний» поток) - в міжтрубний простір.

Через те, що в теплообміннику не змінюється склад матеріальних потоків:

G_Г^К = G_Г^Н; G_Х^К = G_Х^Н C_Х^К = C_Х^Н; C_Гi^К = C_Гi^Н; i = 1,...,NK.

де G – витрата теплоносія; С – концентрація речовини; індекси К і Н позначають кінцевий і початковий стан, а Г і Х – гарячий і холодний потоки.

Кількість теплоти, передана через стінку, дорівнює:

Q = K_TF [(∆t₂-∆t₁)ln(∆t₂/∆t₁)], (1.18)

де К_Т – коефіцієнт теплопередачі; F – площа поверхні теплообміну.

∆t₂ = t_H^Г - t_X^K; ∆t₁ = t_Г^K – t_X^Н.

Кількість теплоти:

- відданої гарячим теплоносієм:

Q = _Г (t_Г^Н – t_Г^К); (1.19)

- прийнятої холодним теплоносієм:

Q = _X(t_X^К -t_X^Н) (1.20)

при цьому водяні еквіваленти дорівнюють:

_Г = G_Г^НС_РГ; _X = G_X^HC_PX.

Рівняння теплового балансу теплообмінника має вигляд:

_Г(t_Г^H - t _Г^K) = _X(t_X^K – t_X^H). (1.21)

З рівняння (1.21) знаходимо:

t_Г^K =t_Г^H – (t_X^K – t_X^H)/N; N = _Г/_X. (1.22)

Через те, що ми зневажаємо втратами теплоти:

_Г (t_Г^H – t_Г^K) = K_TF [(t_Г^H – t_X^K) - (t_Г^K – t_X^H)]/ln[(t_Г^Н - t_X^K)/(t_Г^K – t_X^H)] (1.23)

Підставивши (1.22) в (1.23) і виконавши прості перетворення, одержуємо:

t_X^K = (t_Г^H(N^.В – N) + t_X^H(В – N^.В))/(В – N),

M = K_TF/_Г, В = Ехр((1 – N)М).

Коефіцієнт теплопередачі розраховується по формулі:

K_T = 1 /(1/_TP+∑r_CT+1/_M), (1.24)

де _TP і _M – коефіцієнти тепловіддачі в трубному і міжтрубному просторах; ∑r_CT – сума термічних опорів стінки.

Теплоємності потоків розраховують по формулі:

. (1.25)

Додаток 2

2. Розробка модулів реакторів для автоматизованого розрахунку і проектування складних хіміко-технологічних систем

Проектування хіміко-технологічних систем (ХТС), що базується на методі математичного моделювання, припускає наявність математичних моделей окремих елементів ХТС і рівнянь технологічних зв'язків між ними.

Велику актуальність здобуває задача автоматизації проектування ХТС, тобто створення автоматизованих програм моделювання ХТС. Такі програми названі організуючими чи моделюючими, складаються з двох частин: бібліотеки стандартних програм (модулів) елементів ХТС і програми–диспетчера, що здійснює звертання до того чи іншого модуля з одночасним автоматичним вибором оптимального варіанту конструкції апарата.

Програмні модулі оформляються таким чином, щоб їхня робота не залежала від того, відкіля надходить вхідна інформація. Кожен модуль представляється визначеною обчислювальною процедурою і робить розрахунок параметрів вихідних потоків (витрат, концентрацій компонентів, температур) на підставі відомих значень вхідних і керуючих перемінних.

Етап розробки бібліотеки модулів є найменш формалізованим і найбільш трудомістким. У першу чергу це відноситься до хімічних реакторів - одних з важливих та важкостандартизуємих елементів ХТС.

У хімічному реакторі протікає складний технологічний процес: хімічне перетворення, перенесення і перемішування реагуючих речовин і продуктів реакції, передача тепла. У залежності від того, які властивості реактора необхідно досліджувати, для того самого реактора може бути обрано кілька різних моделей.

Нижче наведні лабораторні роботи які призначаються студентам для самостійного розрахунку найбільш розповсюджених у хімічній технології неорганічних речовин хімічних реакторів:

• каскаду реакторів ідеального змішування;

• змішувача потоків;

• проточного ізотермічного реактора витиснення зі складною хімічною реакцією в реакційному обсязі;

• ізотермічного реактора ідеального змішування зі складною хімічною реакцією в реакційному обсязі.

Розрахунок каскаду реакторів ідеального змішування (РІЗ) інтераційним методом

Хімічні процеси в безвідходних виробництвах мають самостійне значення для одержання цільових продуктів основного хімічного виробництва і для допоміжних процесів – очищення газових викидів, стічних вод і твердих відходів.

У промисловій практиці з технологічних розумінь нерідко потрібно забезпечити повне перемішування і такий ступінь завершення процесу, що в одиничному реакторі досягти неможливо. У такому випадку використовують ланцюжок послідовно з'єднаних реакторів ідеального змішування чи каскад реакторів. Каскади реакторів широко застосовуються в хімічній технології, зокрема, для окислювання SO₂ в SO₃, хлорування бензолу, очищення хімстоків та інших процесах.

Розрахунок каскаду реакторів ідеального змішування ітераційним методом на ЕОМ

Для розрахунків каскаду реакторів, у яких швидкість реакції є функцією концентрації вихідної речовини, найбільш зручно використовувати формулу Ньютона:

,

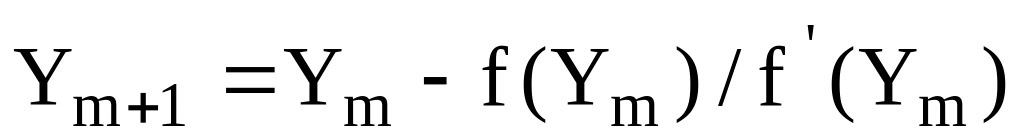(2.1)

де m – номер ітерації; Ym – будь-яке наближення кореня функції;

– наступне, більш точне, значення шуканого кореня;

– функція, корені якої визначаються; – її похідна.

Загальне рівняння матеріального балансу для i-го реактору ідеального змішування має вигляд:

. (2.2)

Для стаціонарного режиму час перебування можна визначити по формулі:

, (2.3)

де Vpі – об’єм i-го реактору;  – об'ємна швидкість; – швидкість реакції по і-ому компоненту, яка розраховується по рівнянню:

, (2.4)

де р – порядок реакції.

У випадку каскаду реакторів рівного об’єму τi = τ1 (i = 1, 2, …,n – номер реактора) справедлива рівність:

.

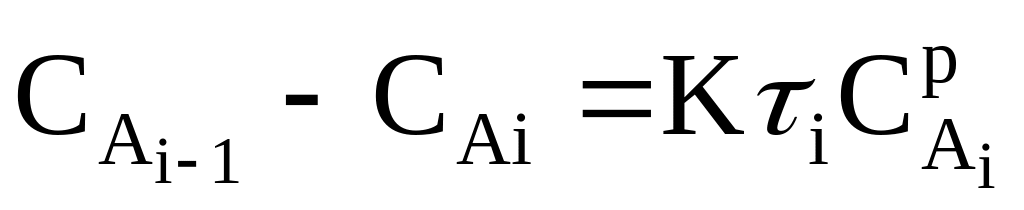(2.5)

Позначимо частку непрореагованої речовини в і-му реакторі: . Тоді ступінь перетворення дорівнює:

.

У результаті нескладних перетворень рівняння (2.3) приймає вид:

.

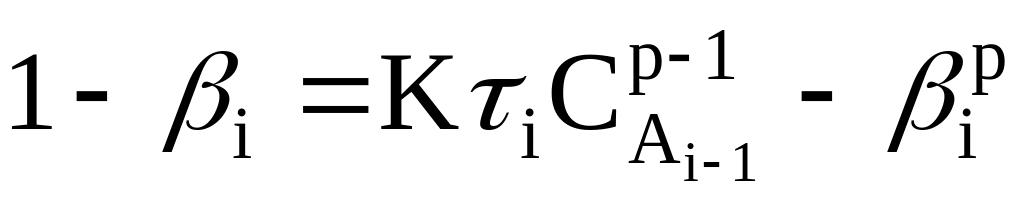(2.6)

Рівняння (1.6) можна записати у вигляді деякої функції:

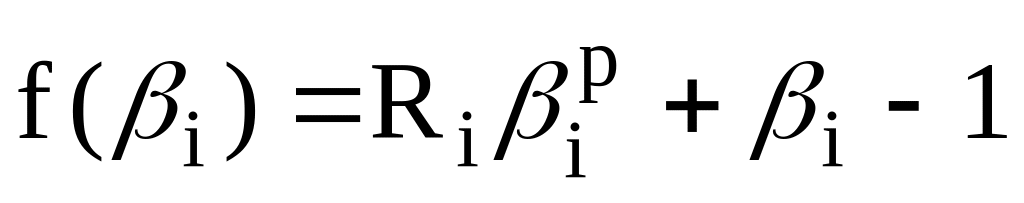, де .

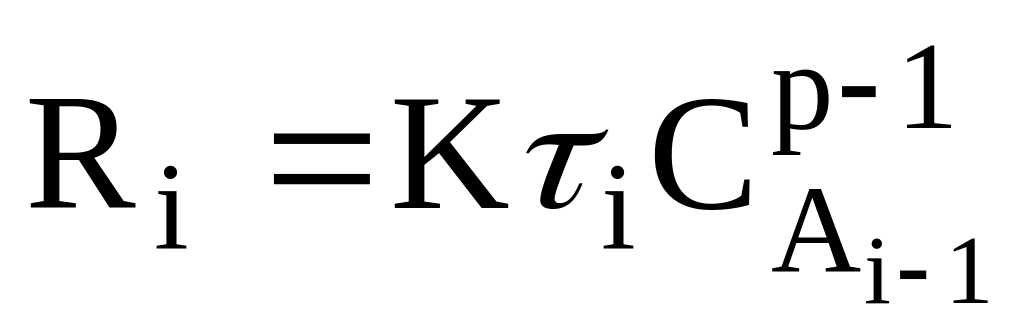(2.7)

Визначення ступеню перетворення в реакторах зводиться, таким чином, до находження кореня рівняння (2.7).

Рішення такої задачі зручно виконувати методом інтерації, використовуючи формулу Ньютона:

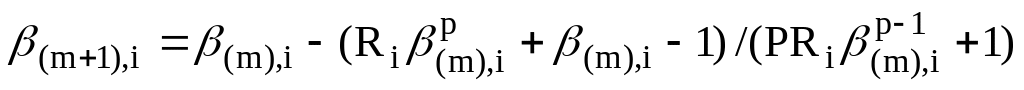
(2.8)

Формула (1.8) дозволяє обчислити для будь-якого порядку реакції р. Як початкове наближення можна прийняти =1. Частку непрореагованої речовини у вихідному потоці каскаду РІЗ розраховуємо по формулі:

,

(2.9)

чи к = 1.2.3.....n-1.n.

Формули (2.7 – 2.9) є вихідними при складанні програми на ЕОМ на базі яких проводять обчислення значень _і, _k, C_Ai. Точність обчислень _і по формулі (2.8) вибирається в залежності від характеру задачі. Для інженерних розрахунків приймаємо, що  =0,001.

Розрахунок змішувача потоків ітераційним методом

При складанні математичного опису змішувача потоків (рис.2.1) скористаємося наступними допущеннями:

• структура потоку в апараті відповідає режиму ідеального змішування;

• режим змішування в апараті – сталий;

• в реакційному об’єму апарата відсутні джерела і стоки речовини і теплоти;

• число потоків, що змішуються, n = 2; (при необхідності змішування більшого числа потоків у схему можна включити декілька послідовно з'єднаних змішувачів);

• теплоємності компонентів i-го потоку розраховується при температурі цього потоку.

Рис.2.1. Схема змішувача потоків

Gj, tj, Cj – витрата, температура і вектор концентрації j-го технологічного потоку.

Загальне рівняння матеріального балансу має вигляд:

,

де G – витрата вихідного потоку; G1, G2, – витрати вхідних потоків.

Рівняння матеріального балансу для i-го компоненту має вигляд:

,

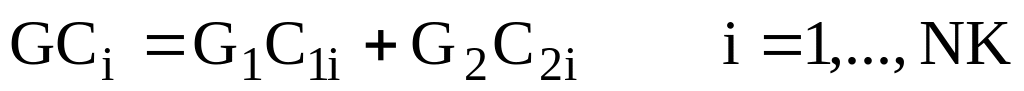(2.10)

де C1 – масова частка i-ої речовини у вихідному потоці;

C1i, C2і – масові частки і-ої речовини в першому і в другому вхідних потоках;

NK – число речовин у потоці.

Очевидно, що:

.

Рівняння теплового балансу має вигляд:

,

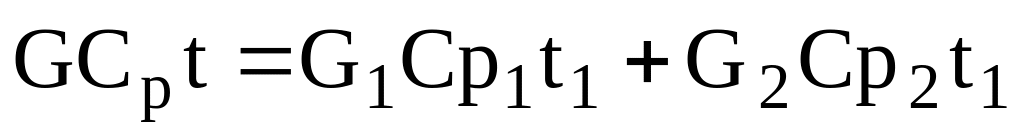(2.11)

де Сp – питома теплоємність вихідного потоку; t – температура вихідного потоку; Сp1, Сp2 – питомі теплоєності вхідних потоків; t1, t2 – температури вхідних потоків.

Звідси:

.

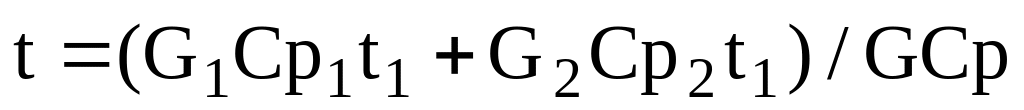(2.12)

Температурна залежність питомої теплоємності i-ої речовини в j-му потоці може бути представлена як функція температури:

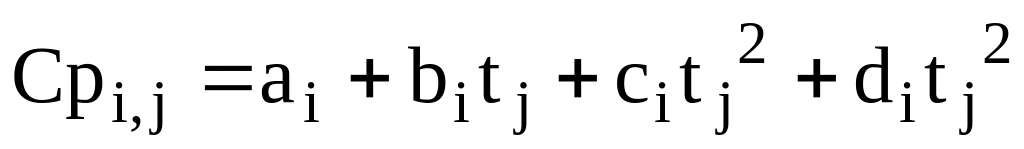
(2.13)

де a, b, c, d – емпірічні коефіцієнти, знайдені для кожної речовини.

Теплоємність j-го потоку обчислюється за правилом адитивності:

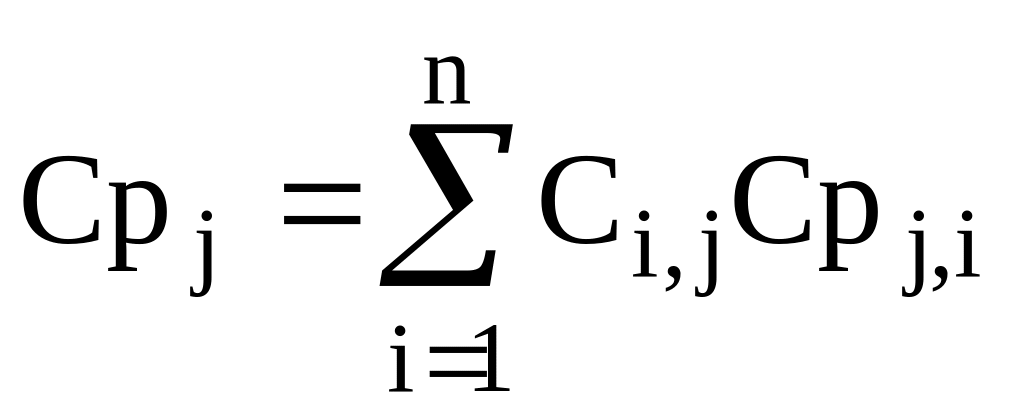
(2.14)

Для вирішення рівняння (2.12) скористуємось методом простої ітерації:

t_k+1 = (G₁Cp₁(t₁)t₁ + G₂Cp₂(t₂)t₂)/(GCp(t_k),

де k = 0,1,2,... – номер ітерації.

Умови закінчення розрахунку: |t_k-1 - t_k| < .