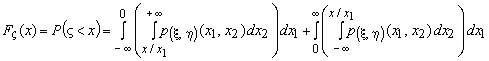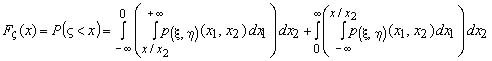- •1. Приведите классическое определение вероятности и укажите, при соблюдении каких условий оно применимо.
- •2. Исходя из трех аксиом теории вероятностей, докажите, что вероятность любого события подчиняется неравенству р(а)?1
- •5. Если появление события в непременно влечет за собой появление события а, то как в этом случае соподчинены противоположные им события ? и b?
- •8. Приведите пример какого-либо опыта с конечным числом элементарных исходов, в условиях которого нельзя исчислять вероятности событий по формуле классического определения вероятности
- •9. Приведите известные вам формулы комбинаторики, которые используются при непосредственном исчислении вероятности по её классическому определению
- •10. Приведите определение условной вероятности
- •11. Зависимость и независимость двух событий (определение)
- •12. Теорема умножения вероятностей для зависимых и независимых событий (формулировка
- •20. Сформулируйте условия, при выполнении которых применяется теорем Байеса. Приведите формулировку и краткое доказательство этой теоремы
- •20. В каком документе закреплено право граждан свободно искать, передавать, производить и распространять информацию
- •21. Функция распределения случайной величины и её свойства
- •22. Функция плотности распределения вероятности и её свойства
- •23. Ряд распределений дискретной случайной величины и его свойство
- •24. Математическое ожидание дискретной случайной величины и его свойства
- •25. Дисперсия дискретной случайной величины и её свойства. Среднее квадратичное отклонение св
- •26. Математическое ожидание непрерывной случайной величины и его свойства
- •27. Дисперсия непрерывной случайной величины и её свойства. Среднее квадратическое отклонение св
- •28. Начальные и центральные моменты случайных величин. Выражение мат.Ожидания и дисперсии св через моменты
- •30. На основе закона распределения альтернативно распределенной случайной величины получить выражение для математического ожидания биномиально распределенной случайной величины
- •31. На основе закона распределения альтернативно распределенной случайной величины получить выражение для дисперсии биномиально распределенной случайной величины
- •32. Случайная величина принимает целые значения в промежутке от 0 до n с равной вероятностью. Вывести выражение для математического ожидания этой случайной величины
- •37. Вывести выражение для дисперсии случайной величины, распределенной по закону Пуассона
- •38. Вывести выражение для математического ожидания случайной величины, распределенной по геометрическому закону
- •43. Плотность распределения и функция распределения равномерной случайной величины, ее числовые характеристики
- •44. Плотность распределения и функция распределения показательной случайной величины. Ее числовые характеристики
- •45. Плотность распределения и функция распределения нормальной случайной величины (распределение Гаусса), ее числовые характеристики
- •46. Функция Лапласа, ее свойства
- •47. Вероятность попадания нормально распределенной случайной величины на отрезок, правило «трех сигм»
- •48. Функции случайных величин и их числовые характеристики
- •49. Числовые характеристики случайных величин, распределенных по равномерному, показательному и нормальному законам (значения мат. Ожидания и дисперсии)
- •50. Дайте определение совместной функции распределения двумерной случайной величины и укажите ее свойства. Обоснуйте эти свойства и/или приведите примеры их выполнения
- •55. Доказать локальную предельную теорему Муавра-Лапласа
- •56. Доказать интегральную предельную теорему Муавра-Лапласа
- •57. Доказать теорему Бернулли о сходимости относительной частоты появления события к вероятности этого события
- •58. Доказать неравенство Чебышева
- •59. Доказать теорему Чебышева
- •60. Понятие генеральной совокупности, выборки из нее. Представление выборки в виде вариационного ряда. Определение вариационного ряда
- •61. Эмпирическая функция распределения, ее свойства, способ построения по выборке
- •62. Понятие оценок числовой характеристики или параметра случайной величины. Свойства оценок
- •63. Нахождение несмещенной оценки генеральной средней (математического ожидания) случайной величины
- •64. Нахождение несмещенной и смещенной оценок генеральной дисперсии случайной величины
- •66. Оценка плотности распределения выборки, ее свойства, способ построения
- •67. Понятие точечных и интервальных оценок (доверительных интервалов) параметров случайной величины. Определения. Примеры
- •68. Свойства точечных оценок параметров: несмещенность, состоятельность, эффективность (определения)
- •69. Определение и свойства оценок: выборочного среднего, выборочной дисперсии и исправленной выборочной дисперсии
- •70. Отличие относительной частоты события от его вероятности по предельной теореме Бернулли (по следствию из теоремы м-л)
- •71. Выборочный коэффициент ковариации (формула)
- •72. Доказать, что выборочное среднее является состоятельной и несмещенной оценкой математического ожидания
- •73. Доказать, что выборочная дисперсия является смещенной оценкой дисперсии
- •74. Доказать, что исправленная выборочная дисперсия является несмещенной оценкой дисперсии
- •75. Какими понятиями определяется интервальная оценка параметра? Какая существует между ними связь в виде формулы?
- •80. Назначение и суть метода моментов и метода максимального правдоподобия
- •81. Сформулируйте основной принцип статистической проверки гипотез
- •82. Что такое ошибка 1 -го рода?
- •88. Что такое критерий согласия?
- •90. Модель парной линейной регрессии: уравнение и основные вероятноcтные допущения
44. Плотность распределения и функция распределения показательной случайной величины. Ее числовые характеристики
08 января 2008 Манакова Юля |
F(x) = 0, x<0; = 1-e^-λx, x>=0. f(x) = 0, x<0; = λe^-λx, x>=0. p(a<X<b)=(e^-a) –(e^-b). M(X)= ∫ от 0 до ∞ (xλ e^-λx)dx = -xe^-λx│+ ∫ от 0 до беск (e^-λx)dx= 1\λ(e^-λx)| = 1\λ. D(X) = ∫ от 0 до беск (x^2 * λe^-λx) dx – 1\(λ^2) = - (x^2) e^-λx| +2 ∫ x e ^-λx dx = 1\x^2 |
45. Плотность распределения и функция распределения нормальной случайной величины (распределение Гаусса), ее числовые характеристики
08 января 2008 Манакова Юля |
f(x) = (1\σ *корень из 2π) *е^( - (x-a)^2\2 σ^2) = 1\ σ φ(x-a\ σ). F(x) = (1\σ *корень из 2π)∫от -∞ до х (e^(-(z-a)^2\2 σ^2))dz = 1\2 = Ф0(x-a\ σ). M(X) = (1\σ *корень из 2π) )∫от -∞ до ∞(x*е^( - (x-a)^2\2 σ^2))dx = (1\корень из 2п)∫от -∞ до ∞(tσ+α)e^(-t^2\2)dt = (σ\корень из 2п)∫ t e^(-t^2\2)dt (это =0) = α\корень из 2п )∫ e^(-t^2\2)dt = a. D(X) = (1\σ *корень из 2π) )∫от -∞ до ∞(x-a)^2* e^( - (x-a)^2\2 σ^2) = σ^2. График пл-ти норм распределения называют нормальной кривой (кривой Гаусса). Ф-ция f(x) = (1\σ *корень из 2π) *е^( - (x-a)^2\2 σ^2) определена на всей оси х, расположена над осью 0х (принимает при всех значениях х положителбные значения), предел = 0 (при |x| стрем-ся к беск-ти), гр-к ф-ции симметричен относительно прямой х = а, при х = а максимум = 1\σ *корень из 2π. |
46. Функция Лапласа, ее свойства
08 января 2008 Манакова Юля |
Функцией Лапласа называется функция вида Ф(Х)= 1\корень из 2п ∫от 0 до х (е^(z^2\2))dz Св-ва; 1. Функция Ф(х)—нечетная, т.е. Ф(-х) =-Ф(х) 2. Функция монотонно возрастает, т.е. х2>x1 следовательно, Ф(х2)>Ф(х1) )=-1\2 )=1\2. Ф(-3.Ф(+ |
47. Вероятность попадания нормально распределенной случайной величины на отрезок, правило «трех сигм»
08 января 2008 Манакова Юля |
P(c<=X<=d) = P(c<=X<d)= P(c<X<=d)= P(c<X<d) = Ф0 (d-a\σ) - Ф0 (c-a\σ) Пр-ло 3х сигм: P(|X-a| <3σ) = P (a-3σ<X<a+3σ) = Ф0((a+3σ)-a\ σ) - Ф0((a-3σ)-a\ σ) = Ф0(3) – Ф0(-3) = 2Ф(3) = 0.9973, т.е. вер-ть того, что отклонение по абсолютной в-не будет меньше утроенного среднего квадратического отклонения, равна 0.9973. Если распредел-е изучаемой СВ неизвестно, но условие, указанное в привидённом правиле, выполняется, то есть основание предполагать, что изучаемая в-на распределена норм; в противном случае – нет. |
48. Функции случайных величин и их числовые характеристики
11 января 2008 Мыльникова Сонечка |
||||||||||||||||||||||||||||||||||||
Функции
случайных величин.Плотность
вероятности суммы двух случайных
величин
~ Распределение
произведения двух случайных величин
Если
- случайная величина с областью значений
X
и функция f(x)
определена на множестве X
, то
=
f(x)
- тоже случайная величина. Задача об
отыскании функции распределения
случайной величины
по известной функции распределения
случайной величины
легко решается, если f(x)
- непрерывная монотонно возрастающая
функция. Доказано, что тогда функция
распределения F
(x)
случайной величины
задается формулой F
(x)=F
([f(x)]-1).Здесь
F
(x)
- известная функция распределения
случайной величины
, а символом [f(x)]-1
обозначена функция, обратная к функции
f(x).
Плотность распределения случайной
величины
для дифференцируемой f(x)
вычисляется по формуле
Найдем распределение произведения случайных величин - случайной величины = , которая принимает значения 0, 1, 2, 3, 4, 6, 8. Вычислим соответствующие вероятности:P( = = 0) = P( = 0, = 1) + P( = 0, = 2) + P( = 0, = 3) + P( = 0, = 4) = 0.1;P( = 1) = P( = 1, = 1) =0.1; P( = 2) = P( = 1, = 2) + P( = 2, = 1) =0.15; и т.д.В результате получим распределение случайной величины = :
Для
того чтобы найти распределение
произведения непрерывных случайных
величин,
необходимо выполнить более громоздкие
вычисления.Пусть (
,
) - непрерывный двумерный случайный
вектор с плотностью распределения
p(
)(x1,
x2).
Построим функцию распределения
случайной величины
=
. Согласно определению
Область D={ x1x2 < x, x > 0} изображена на рисунке слева, а область D={ x1x2 < x, x < 0} - справа.
При
x>0
имеем:
.
При
x<0:
|

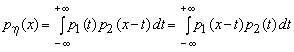 .Распределение
произведения двух случайных
величин Порядок
построения распределения произведения
двух дискретных случайных величин
проще всего объяснить на примере.Пусть
(
,
) - дискретный случайный вектор с
распределением:
.Распределение
произведения двух случайных
величин Порядок
построения распределения произведения
двух дискретных случайных величин
проще всего объяснить на примере.Пусть
(
,
) - дискретный случайный вектор с
распределением: