Формула Тейлора

Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.

Теорема:

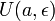
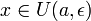
Пусть функция f(x) имеет n + 1 производную в некоторой окрестности точки a,  Пусть  Пусть p — произвольное положительное число, тогд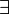а:   точка 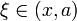  при x < a или  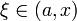 при x > a: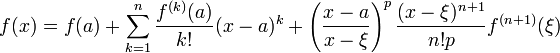

Различные формы остаточного члена

В форме Лагранжа:

В форме Коши:

Ослабим предположения:

• Пусть функция f(x) имеет n − 1 производную в некоторой окрестности точки a

• И n производную в самой точке a, тогда:

 — остаточный член в асимптотической форме (в форме Пеано, в локальной форме)

16

Достаточным условием сходимости ряда Тейлора является бесконечная диффер f(x) и ограниченность производной ¥порядка от f(x) док-во  Rn(x)=f^n+1(c)/(n+1)!(x-a)^n+1 ]|f(c)^n+1| < M | Rn(x)| < M|(x-f)^n+1| /n+1)! M>0 расм ряд  (x-a)+(x-a)^2/2!+…+.(x-a)^n/n!+(x-a)^n+1/(n+1)!  По признаку Деламбера (n→∞)Lim(x-a)^n+1/(n+1)!*(n!/(x-a)^n=(n→∞)Lim|(x-a)|/n+1=0<1 ряд сходится А абсолютный член ряда стремиться к нулу  (n→∞)LimRn(x)=M(n→∞)Lim(x-a)^n+1/(n+1)=0  ряд Макларена для  f(x)=e^x e^x=1+x/1!+x^2/2!+x^n/n!+e^c*x^n+1/(n+1)!- ф-ла Макларена  f^(n)(x)=e^x  f^(0)=1 e^x=1+x/1!+x^2/2!.... (x=1):(n→∞)Lim x^(n+1)* n!/ ((n+1)!*x^n)=0<1 a0+a1*x+…+an*x^n+A_n+1x^n=1 R=(n→∞)Lim(n=1)!/n!= ∞=(n→∞)Lim (an)/a_n+1 X=1 e=1+1+1/2+1/6+R4(x)=16/6+e^c/24 (e-8/3)=e^c/24<3/24=1/8 f(x)=sin(x) f`(x)=cos(x)=sin(x+¶/2) f``(x)=sin(x+2¶/2) f^(n)(x)=sin(x+n*¶/2) sin(x)=x-x^3/3!+x^5/5!+…+(-1)^n8x^2n+1)/(2n+1)!

17

Разложение некоторых функций в ряд Маклорена

 

18

. Применение степенных рядов

Разложения 1-7 из предыдущего пункта позволяют, используя соответствующее разложение, вычислять приближенно значения функций, интегралы, приближенно интегрировать дифференциальные уравнения. Пример 9. С помощью степенного ряда вычислить  с точностью до 0,0001. Решение. Разложим функцию в степенной ряд: Тогда имеем:  . Так как получившийся ряд является знакочередующимся, то сумма знакочередующегося ряда не превосходит первого члена такого ряда. Ясно, что часть ряда, которую в задаче следует отбросить, также является знакочередующимся рядом и его сумма не превзойдет модуля первого отброшенного члена ряда. Таким образом, первый отброшенный член ряда должен быть меньше заданной погрешности, то есть 0,0001. Вычислив еще несколько членов ряда  , видим, что  . Отбросив этот и следующие за ним члены ряда, получим .

19

Тригонометрический ряд Фурье — представление произвольной функции f с периодом τ в виде ряда

(1)

или используя комплексную запись, в виде ряда:

.

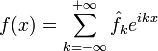20

    Коэффициенты Фурье функции f периода   

либо

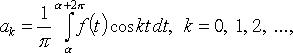
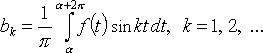
21