
- •Необходимый признак сходимости числового ряда.
- •Предельная форма
- •Доказательство
- •Интегральный признак
- •7. Непрерывность суммы равномерно сходящегося ряда из непрерывных функций. Почленное интегрирование и дифференцирование ряда
- •Формула Тейлора
- •Различные формы остаточного члена
- •Разложение некоторых функций в ряд Маклорена
- •Яды Фурье для четных и нечетных функций
- •Двойной интеграл
- •I. Вычисление двойных интегралов с помощью двойного интегрирования.
- •Определения
- •Поверхностный интеграл первого рода [править]Определение
- •Поверхностный интеграл второго рода [править]Определение
Предельная форма
Условие радикального признака равносильно следующему:
![]()
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
-
Если для ряда
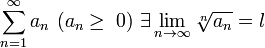 ,
то
,
тоесли
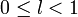 ряд
сходится,
ряд
сходится,если l > 1 ряд расходится,
если l = 1 вопрос о сходимости ряда остается открытым.
Доказательство
1.
Пусть l <
1.
Очевидно, что существует такое ![]() ,
что l +
ε < 1.
Поскольку существует предел
,
что l +
ε < 1.
Поскольку существует предел ![]() ,
то подставив в определение предела
выбранное εполучим:
,
то подставив в определение предела
выбранное εполучим:
![]()
Раскрыв модуль, получаем:
![]()
![]()
(l − ε)n < an < (l + ε)n
Поскольку l +
ε < 1,
то ряд ![]() сходится.
Следовательно, по признаку
сравнения ряд
тоже
сходится.
сходится.
Следовательно, по признаку
сравнения ряд
тоже
сходится.
2. Пусть l > 1. Очевидно, что существует такое , что l − ε > 1. Поскольку существует предел , то подставив в определение предела выбранное εполучим:
Раскрыв модуль, получаем:
(l − ε)n < an < (l + ε)n
Поскольку l −
ε > 1,
то ряд ![]() расходится.
Следовательно, по признаку
сравнения ряд
тоже
расходится.
расходится.
Следовательно, по признаку
сравнения ряд
тоже
расходится.
Интегральный признак
Пусть
тогда
ряд
и
несобственный интеграл
|
7
Если P<1 ряд расходится
p>1 ряд сходится
8
Т.
(признак Лейбница): Если для ряда![]()
выполняются
условия:![]() то
этот ряд сходится, причем его сумма
то
этот ряд сходится, причем его сумма![]() и
и![]()
Рассмотрим
частичную сумму![]() члены
которой сгруппируем по два:
члены
которой сгруппируем по два:
![]()
В силу условия
1)
разности в скобках положительны, поэтому
последовательность![]() возрастающая
и
возрастающая
и![]()
Перегруппируем
члены![]()
![]()
отсюда![]() Возрастающая
и ограниченная последовательность
имеет предел
Возрастающая
и ограниченная последовательность
имеет предел![]()
Для
последовательности нечетных сумм![]() в
силу условия
в
силу условия
2) имеем
![]()
Таким
образом,![]() и
ряд сходится
и
ряд сходится
9
Сходящийся ряд ![]() называется
сходящимся абсолютно, если сходится
ряд из модулей
называется
сходящимся абсолютно, если сходится
ряд из модулей ![]() ,
иначе — сходящимся условно.
,
иначе — сходящимся условно.
Аналогично,
если несобственный
интеграл ![]() от
функции сходится, то он называется
сходящимся абсолютно или условно в
зависимости от того, сходится или нет
интеграл от ее модуля
от
функции сходится, то он называется
сходящимся абсолютно или условно в
зависимости от того, сходится или нет
интеграл от ее модуля ![]() .
.
В случае общего нормированного пространства модуль в определении заменяется на норму.
Признаки абсолютной сходимости
[править]Признак сравнения
Если ![]() при
при ![]() ,
то:
,
то:
если ряд
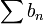 сходится,
то ряд
сходится
абсолютно
сходится,
то ряд
сходится
абсолютноесли ряд расходится, то ряд расходится
Согласно критерию
Коши, 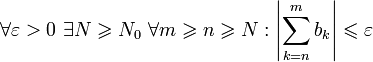 .
Значит,
.
Значит, 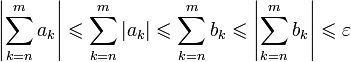 ,
и по критерию Коши ряд
сходится.
Второе утверждение следует из первого,
так как если бы ряд
сходился,
то и ряд
сходился
бы.
,
и по критерию Коши ряд
сходится.
Второе утверждение следует из первого,
так как если бы ряд
сходился,
то и ряд
сходился
бы.
[править]Признак сходимости рядов с монотонно убывающими членами
Пусть ![]() .
Тогда ряд
сходится
тогда и только тогда, когда сходится
ряд
.
Тогда ряд
сходится
тогда и только тогда, когда сходится
ряд ![]()
Условная сходимость
[править]
У этого термина существуют и другие значения, см. Сходимость.
Ряд
называется условно сходящимся,
если сам он сходится, а ряд, составленный
из абсолютных
величин его
членов, расходится. То есть, если ![]() существует
(и не бесконечен), но
существует
(и не бесконечен), но ![]() .
.
10
Функциональный
ряд, его сходимость.
Рассмотрим ряд,  ,
членами которого являются функции,
определенные на промежутке
,
членами которого являются функции,
определенные на промежутке ![]() .
При каждом фиксированном
.
При каждом фиксированном ![]() имеем
числовой ряд, сходимость которого может
быть исследована рассмотренными ранее
методами. Сумма функционального
ряда
также
является функцией от х:
имеем
числовой ряд, сходимость которого может
быть исследована рассмотренными ранее
методами. Сумма функционального
ряда
также
является функцией от х: ![]() .
По определению предела последовательности:
если для
.
По определению предела последовательности:
если для ![]() можно
указать номер
можно
указать номер ![]() (
что интересно, для каждого фиксированного
- свой номер, т.е.
(
что интересно, для каждого фиксированного
- свой номер, т.е. ![]() ),
такой, что для
),
такой, что для ![]() выполняется
неравенство
выполняется
неравенство ![]() ,
то это и означает, что функциональный
ряд сходится к функции
,
то это и означает, что функциональный
ряд сходится к функции![]() .
Множество
.
Множество ![]() ,
для которого это выполняется, называется
областью сходимости функционального
ряда.
,
для которого это выполняется, называется
областью сходимости функционального
ряда.
ПРИМЕР 1. Нахождение области сходимости функционального ряда.
![]()
Равномерная
сходимость функционального ряда.
Пусть
,
т.е. функциональный ряд сходится. Если
для
можно
указать номер
независимо
от ![]() ,
такой, что для
,
такой, что для![]() выполняется
неравенство
,
то говорят, что функциональный ряд
сходится равномерно на множестве .
выполняется
неравенство
,
то говорят, что функциональный ряд
сходится равномерно на множестве .
ПРИМЕР 2. Изучение сходимости функционального ряда.
Исследование
на равномерную сходимость.
Признак Вейерштрасса равномерной
сходимости функционального ряда: если
существует сходящийся числовой ряд ![]() с
положительными членами, такой, что для
всех
с
положительными членами, такой, что для
всех ![]() ,
начиная с некоторого номера и
всех
выполняется
неравенство
,
начиная с некоторого номера и
всех
выполняется
неравенство![]() ,
то функциональный ряд
сходится
на
равномерно.
Числовой ряд
в
этом случае называют мажорантой для
функционального ряда.
,
то функциональный ряд
сходится
на
равномерно.
Числовой ряд
в
этом случае называют мажорантой для
функционального ряда.
11
Равномерная
сходимость последовательности функций (отображений)
— свойство последовательности ![]() ,
где X —
произвольное множество, Y =
(Y,d) —метрическое
пространство,
,
где X —
произвольное множество, Y =
(Y,d) —метрическое
пространство, ![]() сходится
к функции (отображению)
сходится
к функции (отображению) ![]() ,
означающее, что для любого
существует
такой номер Nε,
что для всех номеров n > Nε и
всех точек
,
означающее, что для любого
существует
такой номер Nε,
что для всех номеров n > Nε и
всех точек ![]() выполняется
неравенство
выполняется
неравенство
![]()
Обычно
обозначается ![]() .
.
Это условие равносильно тому, что
![]()
12

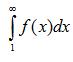 сходятся
или расходятся
одновременно.
сходятся
или расходятся
одновременно.