7. Непрерывность суммы равномерно сходящегося ряда из непрерывных функций. Почленное интегрирование и дифференцирование ряда

 

Теорема. Пусть    на  . Пусть  . Тогда  .

Доказательство. Требуется доказать, что   функция    непрерывна в точке  , т.е.  . Зафиксируем произвольное  . Ввиду равномерной сходимости  . В частности,  . По условию, при любом    функция   - непрерывная. Значит,  . При выбранных    имеем:    , что и требовалось доказать. Вычисление определённого интеграла. Формула Ньютона-Лейбница.

Следствие. Сумма равномерно сходящегося ряда, члены которого являются непрерывными функциями, есть непрерывная функция.

Доказательство. Применим предыдущую теорему к последовательности частичных сумм ряда.

Теорема. (почленное интегрирование ряда). Пусть ряд   равномерно сходится к своей сумме   на отрезке    и все  . Тогда     .

Доказательство. Обозначим при произвольном  ,  . Тогда   - непрерывная функция и, т.к. по предыдущей теореме   - непрерывная функция,    - также непрерывная функция. Тогда 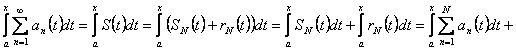   . Для доказательства теоремы достаточно доказать, что   при  , т.к., по определению,    . Но  . Поэтому при      и требуемое утверждение доказано.

Замечание. Для функциональных последовательностей эта теорема формулируется следующим образом: Пусть   на  . Пусть  . Тогда  .

Теорема. (о почленном дифференцировании ряда).

Пусть:

1.                   ;

2.                  Ряд   сходится на    (и пусть его сумма обозначена  );

3.                  Ряд   равномерно сходится на  .

Тогда   или, иными словами,  .

Доказательство. Обозначим    - сумму ряда  . Тогда    - непрерывная на   функция. Поэтому    существует ее интеграл от   и он, по предыдущей теореме, равен    . Значит,    или  .

Замечание. Соответствующая теорема для последовательностей может быть сформулирована так: Пусть  . Пусть  ,   и пусть  ,  . Тогда  , или  .

13

Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:

в котором коэффициенты a_n берутся из некоторого кольца R.

(Нильс Хенрик Абель (1802 – 1829) – норвежский математик)

[an error occurred while processing this directive]

  Теорема. Если степенной ряд   сходится при x = x₁ , то он сходится и притом абсолютно для всех  .

 

  Доказательство. По условию теоремы, так как члены ряда ограничены, то

где k- некоторое постоянное число. Справедливо следующее неравенство:

Из этого неравенства видно, что при x<x₁ численные величины членов нашего ряда будут меньше ( во всяком случае не больше ) соответствующих членов ряда правой части записанного выше неравенства, которые образуют геометрическую прогрессию. Знаменатель этой прогрессии   по условию теоремы меньше единицы, следовательно, эта прогрессия представляет собой сходящийся ряд.

Поэтому на основании признака сравнения делаем вывод, что ряд   сходится, а значит ряд   сходится абсолютно.

 

Таким образом, если степенной ряд  сходится в точке х₁, то он абсолютно сходится в любой точке интервала длины 2  с центром в точке х = 0.

 

Следствие. Если при х = х₁ ряд расходится, то он расходится для всех  .

 

Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что   ряд абсолютно сходится, а при всех  ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.

Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.

Радиус сходимости может быть найден по формуле:

 Пример. Найти область сходимости ряда 

Находим радиус сходимости  .

Следовательно, данный ряд сходится прилюбом значении х. Общий член этого ряда стремится к нулю.

14

Теорема 2.2. (непрерывность суммы ряда). На любом отрезке  целиком лежащем внутри интервала сходимости степенного ряда (1.2), сумма ряда есть непрерывная функция.

Доказательство. Каждая частичная сумма степенного ряда, очевидно, является непрерывной функцией. По теореме 2.1 на любом отрезке целиком лежащем внутри интервала сходимости ряда сходимость является равномерной. Сумма ряда, являющаяся пределом равномерно сходящейся последовательности непрерывных функций, сама является непрерывной функцией. Теорема доказана.

Теорема 2.3. (Почленное интегрирование степенного ряда). Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то последовательность интегралов от частичных сумм ряда сходится к интегралу от суммы ряда.

Доказательство следует из аналогичной теоремы для функциональных рядов (теорема 2.2 предыдущей лекции).

Теорема 2.4. (Почленное дифференцирование степенного ряда). Пусть степенной ряд

   (2.1)

 имеет радиус сходимости R. Тогда ряд

   (2.2) 

полученный в результате почленного дифференцирования ряда (2.1), также имеет радиус сходимости R. Производная суммы ряда (2.1) равна сумме ряда (4.2):   

Из теоремы 2.4 следует

Теорема 2.5. Степенной ряд в пределах его интервала сходимости можно дифференцировать почленно любое число раз. При этом радиусы сходимости всех рядов, полученных дифференцированием данного ряда, совпадают с радиусом сходимости этого ряда.

Наряду со степенными рядами вида

   (2.3)

 будем рассматривать ряды вида

   (2.4)

Ясно, что подстановкой   ряд (2.4) превращается в ряд (2.3). Поэтому ряд (2.4) сходится при  ( R – радиус сходимости ряда (2.3)). Итак, интервал сходимости ряда (2.4) есть 

Все свойства, которыми обладает ряд (2.3) в интервале (-R,R), переносятся на ряд (2.4) в интервале   

15