Вывести 1 замечательный предел:
П
усть
,
.
Ясно, что
,
но
,
т.е.
,
т.к.
.
Билет №8-1. Доказать теорему Бернулли-Лопиталя для предела отношения двух бесконечно малых функций.
Теорема. Пусть ф-ции f(x)
и g(x)
определены и дифференцируемы в
,
представляют собой б.м.ф. при
,
причем
в
.
Если
.
Доказательство: Рассмотрим {
.
Доопределим по непрерывности данные
функции нулем в точке a
(f(a)=0, g(a)=0).
Тогда на [a,
]
функции f(x)
и g(x)
непрерывны, на (a;
)
f(x) и g(x)
дифференцируемы. По теореме Коши
при
по условию теоремы
>
Замечание 1: точка а может быть бесконечной,
тогда
или
Формулировка: пусть f(x)
b g(x)
определены и дифференцируемы на
и представл. Б.м.ф. при
,
причем
Если
Замечание 2: если
и
удовлетворяют всем условиям Б-Л и
,
то
и т. д.
Билет №8-2. Векторная функция скалярного аргумента: и её производная. Касательная к пространственной кривой. Теорема о производной вектор-функции постоянной длины.
Рассмотрим [a,b].
Пусть любому
поставлен
в соответствии некоторый вектор
,
тогда говорят, что на [a,b]
задана векторная функция скалярного
аргумента.
Пусть задана ортонормированная система
координат с базисом
,
тогда
Функции x(t), y(t), z(t)- скалярные функции действительного аргумента – координатные функции для вектор-функции .
Геометрический смысл векторной функции:
Ф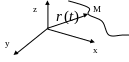
ункции
соответствует
некоторая кривая
Такое представление кривой называют
годографом.
называется пределом функции
скалярного
аргумента при
если:
.
Рассмотрим приращение векторной функции,
придадим t приращение
,
тогда
.
Производной
в
точке
называется предел разностного отношения
при
,
.
,
.
=
=
Пусть
.
Предельное положение секущей
при
называют касательной к кривой Г в точке
.
. Тогда при
касательная в точке
параллельна вектору
.
Уравнение касательной:
.
-
каноническое уравнение касательной.
Теорема: Пусть векторная функция
скалярного аргумента
,
- является непрерывно-дифференцируемой
функцией на
,
которой соответствует некоторая кривая
Г:
.
Тогда
длина
дуги Г удовлетворяет:
(при этом Г имеет конечную длину).
Доказательство:
,
где
,
по условию теоремы, функция
непрерывно-дифференцируема, значит
на отрезке
- непрерывная функция.
,
(по 1 теореме Вейерштрасса).
при
.
Билет №9-1. Формула Тейлора с остаточным членом в форме Пеано, Лагранджа.
Теорема. Пусть ф-ция F(x)
определена в
и имеет в
производные до (n+1)-го
порядка включительно. Пусть x
– произвольное значение аргумента
ф-ции из
,
тогда для произвольного значения P,
p>0
,
расположенная между a и
x, такие что справедлива
следующая формула:
.
.
Формула называется формулой Тейлора с
центром в точке a;
-
остаточный член в формуле Тейлора в
общем виде.
эта функция – многочлен степени n
– многочлен Тейлора с центром в точке
а.
Обозначим
.
Рассмотрим вспомогательную функцию
.
,
где
Покажем, что на [a;x]
удовлетворяет
всем условиям теоремы Ролля:
непрерывность на [a;x];
дифференцируема на (a;x);
;
;
;
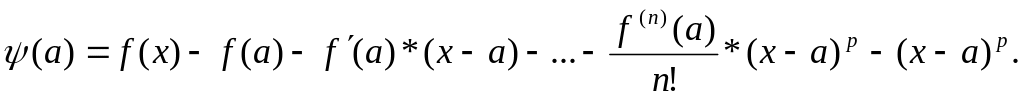
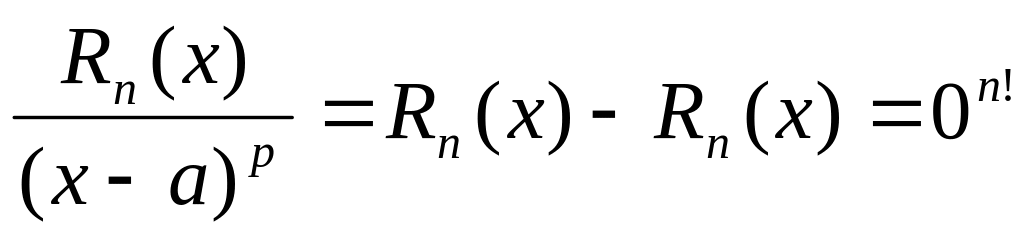
Теорема. Остаточный член в форме Тейлора
представляет собой б. м. более высокого
порядка малости, чем
при
.
,
.
Доказать:
;
=0;
;
n раз применяем пр. Б-Л.=
Такую запись остаточного члена называют ост. Чл. В форме Пеано: .
Рассмотрим другие формы записи остаточного
члена.
,
1) p=n+1, тогда
- остаточный член в форме Лагранжа.
2) p=1 – в форме Коши:
Число
в формуле Лагранжа и формуле Коши разные,
т. К. зависят от P. Остаточный
член в форме Лагранжа и Коши представляют
собой погрешность, которую мы получаем,
заменяя функцию f(x)
ее многочленом Тейлора. Если нас
интересует порядок малости такой замены
при
,
то он совпадает с порядком малости
остаточного члена в форме Пеано.
Оценка остаточного члена в форме Лагранжа.
Пусть функция имеет производную любого
порядка в
и эти производные ограничены одной и
той же константой M.
;
Билет №9-2.
Свойства б.м. функций.
Сумма конечного числа б.м.ф. при представляет собой б.м. функцию при .
- б.м.ф.
Произведение конечного числа б.м.ф. при представляет собой б.м. функцию при .
- б.м.ф.
Пусть - б.м.ф. при , а - ограничена в , тогда
- б.м.ф. при
.
.
Пусть
,
тогда
,
для
,
тогда
- б.м.ф. при
.
Билет №10.
Доказать первое достаточное условие экстремума функции.
Пусть функция определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
Доказательство: Рассмотрим точку х из указанной окрестности, тогда на :
- непрерывна.
на - дифференцируема.
По т. Лагранжа , где , т.к. , то
на : где ,