Постсинаптическая активность ( ) возникает при отсутствии существен­ной предсинаптической активности ( ).

Такое поведение можно рассматривать как форму временной конкуренции между входными моделями.

Существует строгое физиологическое доказательство'' реализации принципа обу­чения Хебба в области мозга, называемой гипокампусом (hippocampus). 'Эта область играет важную роль в некоторых аспектах обучения и запоминания. Физиологические результаты еще раз подтверждают правильность постулата обучения Хебба.

17.Парадигмы обучения нс. Конкурентное обучение. Математическая модель

При конкурентном обучении, в отличие от, например, обучения Хебба, в фиксированный момент времени в возбужденном состоянии может находиться только один нейрон выходного слоя. В связи с этим конкурентные сети часто применяются для решения задач классификации входных образов.

Конкурентное обучение строится на основании следующих принципов:

• Все нейроны выходного слоя одинаковы и имеют в начальный момент времени случайные значения весов.

• Существует предельное значение выходного сигнала каждого нейрона.

• Существует механизм, определяющий нейрон, победивший в борьбе за право генерировать выходной сигнал. Принцип конкуренции можно сформулировать как «победитель получает все»

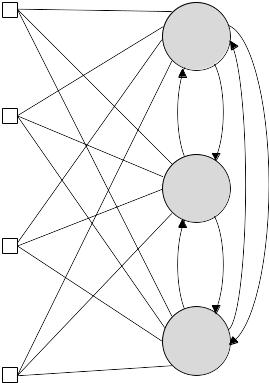
Механизм конкуренции может формироваться за счет введения отрицательных обратных связей, обеспечивающих латеральное торможение, когда каждый нейрон стремится затормозить связанные с ним нейроны (рис. 7.11).

Для того, чтобы нейрон выходного слоя победил в конкурентной борьбе, его индуцированное локальное поле должно быть максимальным среди всех нейронов выходного слоя. Таким образом, выходной сигнал нейрона можно записать в виде:

. (7.22)

Если предположить, что синаптические веса конкурирующих нейронов положительны и выполняются следующие нормировки:

, (7.23) (7.24)

Правило конкурирующего обучения можно записать в виде:

Данное правило обеспечивает смещение вектора синаптических весов в сторону вектора входного сигнала.

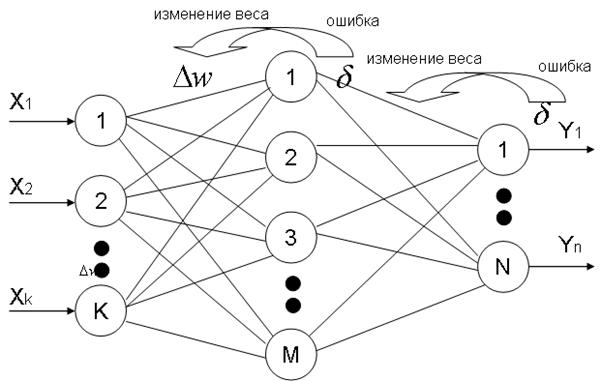
18.Парадигмы обучения нс. Обучение методом обратного распространения ошибки. Математическая модель

Алгоритм обратного распространения ошибки

В этом алгоритме происходит распространение ошибки от выходов НС ко входам, то есть в направлении обратном распространению сигналов обычном режиме работы. Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является величина:

где реальное выходное состояние нейрона выходного слоя N нейронной сети при подаче на ее входы - го образа; - желаемое (идеальное) выходное состояние этого нейрона. Суммирование происходит по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:

• - коэффициент скорости обучения,

Обучение методом обратного распространения ошибки происходит в соответствии со следующими пунктами:

1. Подать на входы НС образец выбранный случайным образом и в режиме обычного функционирования НС рассчитать ее выходы.

2. Рассчитать дельту ошибки для выходного слоя по формуле:

3. Рассчитать изменения весов для выходного слоя N по формуле:

4. Рассчитать ошибки и изменения весов (формула 3) для всех остальных слоев по формулам:

5. Скоректировать все веса нейронной сети по формуле:

6. Если ошибка сети существенна, то перейти на на шаг 1. В противном случае – конец обучения.

Изменение весов нейронной сети можно вести также с помощью формулы:

где - коэффициент инерционности. Эта формула позволяет «гладко» изменять веса, что приводит к понижению перепадов ошибки. Формулу целесообразно применять в конце обучения, когда ошибка близка к заданной.

19. Парадигмы обучения нс. Обучение Больцмана. Математическая модель

Машина Больцмана – нейронная сеть, состоит из стохастических нейронов, каждый из них связан обратной связью со всеми остальными.

Машина Больцмана применяется для решения задач классификации образов ввиду способности находить абсолютный минимум целевой функции.

Простейший пример архитектуры машины Больцмана.

Подразумевается, что в такой сети применяются симметричные синаптические связи. Выделяют два режима функционирования машины Больцмана:

• Скованное состояние, в котором все видимые нейроны находятся в состояниях, определенных внешней средой.

• Свободное состояние, в котором все нейроны могут свободно функционировать.

В процессе функционирования сети выбирается один из свободных нейронов и его состояние изменяется с вероятностью:

,

где - это энергия машины, определяемая соотношением:

,

а - изменение энергии машины, вызванное переключением состояния выбранного нейрона. Многократное повторение этой процедуры приводит к достижению машиной состояния термального равновесия.

Процедура обучения для такой сети состоит из следующих шагов:

1. Вычислить закрепленные вероятности.

1. придать входным и выходным нейронам значения обучающего вектора;

2. предоставить сети возможность искать равновесие;

3. запомнить выходные значения (состояния) для всех нейронов;

4. повторить шаги от а до с для всех обучающих векторов;

5. вычислить вероятность , то есть по всему множеству обучающих векторов вычислить вероятность того, что состояния обоих нейронов равны единице.

2. Вычислить незакрепленные вероятности.

1. предоставить сети возможность «свободного движения» без закрепления входов или выходов, начав со случайного состояния;

2. повторить предыдущий много раз, запоминая состояния всех нейронов;

3. вычислить вероятность , то есть вероятность того, что состояния обоих нейронов равны единице.

3. Скорректировать веса сети следующим образом: , где - изменение веса , а - константа скорости обучения.

Обученная в соответствии с алгоритмом Больцмана нейронная сеть обладает способностью к дополнению входных образов. То есть, если входной вектор с неполной информацией поступает на вход сети, сеть дополнит недостающую информацию.

Основным недостатком алгоритма обучения Больцмана является большая длительность процесса обучения.

20. Персептрон Розенблатта. Алгоритм обучения однослойного персептрона

Персептрон Розенблатта (модель МакКаллока-Питтса)

Персептрон Розенблатта представляет собой искусственный нейрон со ступенчатой функцией активации, который стал отправной точкой для построения первых искусственных нейронных сетей.

Задача, решаемая с помощью персептрона Розенблатта, состоит в классификации векто ра в смысле отнесения его к одному из двух классов и . Вектор относится к классу , если выходной сигнал принимает значение 0, и к классу , если выходной сиг нал равен 1. При этом персептрон разделяет мерное пространство входных сигналов на два полупространства, разделяемых мерной гиперплоскостью, описываемой уравнением:

(7.6)

Эта гиперплоскость называется решающей границей.

В случае, когда размерность пространства входных сигналов , решающая граница это прямая, описываемая уравнением (рис 7.5):

(7.7)

Следует отметить, что персептрон Розенблатта можно использовать для решения весьма ограниченного класса задач, так как он может классифицировать только линейно разделимые входные сигналы.

Алгоритм обучения однослойного персептрона:

Дальше можно не писать, но вот спросить он может

Первый тип ошибки: на выходе персептрона — 0, а правильный ответ — 1. Для того чтобы персептрон выдавал правильный ответ, необходимо, чтобы сумма в правой части (1) стала больше. Поскольку переменные принимают значения 0 или 1, увеличение суммы может быть достигнуто за счет увеличения весов   . Однако нет смысла увеличивать веса при переменных  , которые равны нулю. Таким образом, следует увеличить веса   при тех переменных x_i, которые равны 1.

Правила Хебба :

Первое правило. Если на выходе персептрона получен 0, а правильный ответ равен 1, то необходимо увеличить веса связей между одновременно активными нейронами. При этом выходной персептрон считается активным. Второй тип ошибки: на выходе персептрона — 1, а правильный ответ равен нулю. Для обучения правильному решению данного примера следует уменьшить сумму в правой части (1). Следовательно, необходимо уменьшить веса связей   при тех переменных, которые равны 1 (поскольку нет смысла уменьшать веса связей при равных нулю переменных  ). Необходимо также провести эту процедуру для всех активных нейронов предыдущих слоев. В результате получаем второе правило.

Второе правило. Если на выходе персептрона получена единица, а правильный ответ равен нулю, то необходимо уменьшить веса связей между одновременно активными нейронами.

Таким образом, процедура обучения сводится к последовательному перебору всех примеров обучающего множества с применением правил обучения для ошибочно решенных примеров. Если после очередного цикла предъявления всех примеров окажется, что все они решены правильно, то процедура обучения завершается.

Теорема. Любой персептрон можно заменить другим персептроном того же вида с целыми весами связей.

21. Персептрон Розенблатта. Теорема о сходимости и «зацикливании» персептрона.

Персептрон Розенблатта (модель МакКаллока-Питтса)

Персептрон Розенблатта представляет собой искусственный нейрон со ступенчатой функцией активации, который стал отправной точкой для построения первых искусственных нейронных сетей.

Задача, решаемая с помощью персептрона Розенблатта, состоит в классификации векто ра в смысле отнесения его к одному из двух классов и . Вектор относится к классу , если выходной сигнал принимает значение 0, и к классу , если выходной сиг нал равен 1. При этом персептрон разделяет мерное пространство входных сигналов на два полупространства, разделяемых мерной гиперплоскостью, описываемой уравнением:

(7.6)

Эта гиперплоскость называется решающей границей.

В случае, когда размерность пространства входных сигналов , решающая граница это прямая, описываемая уравнением (рис 7.5):

(7.7)

Следует отметить, что персептрон Розенблатта можно использовать для решения весьма ограниченного класса задач, так как он может классифицировать только линейно разделимые входные сигналы.

Теорема о сходимости персептрона. Если существует вектор параметров  , при котором персептрон правильно решает все примеры обучающей выборки, то при обучении персептрона по вышеописанному алгоритму решение будет найдено за конечное число шагов.

Теорема о "зацикливании" персептрона. Если не существует вектора параметров  , при котором персептрон правильно решает все примеры обучающей выборки, то при обучении персептрона по данному правилу через конечное число шагов вектор весов начнет повторяться.

Таким образом, данные теоремы утверждают, что, запустив процедуру обучения персептрона, через конечное время мы либо получим обучившийся персептрон, либо ответ, что данный персептрон поставленной задаче обучиться не может.

22. Персептрон Розенблатта. Дельта -правило

Персептрон Розенблатта (модель МакКаллока-Питтса)

Персептрон Розенблатта представляет собой искусственный нейрон со ступенчатой функцией активации, который стал отправной точкой для построения первых искусственных нейронных сетей.

Задача, решаемая с помощью персептрона Розенблатта, состоит в классификации векто ра в смысле отнесения его к одному из двух классов и . Вектор относится к классу , если выходной сигнал принимает значение 0, и к классу , если выходной сиг нал равен 1. При этом персептрон разделяет мерное пространство входных сигналов на два полупространства, разделяемых мерной гиперплоскостью, описываемой уравнением:

(7.6)

Эта гиперплоскость называется решающей границей.

В случае, когда размерность пространства входных сигналов , решающая граница это прямая, описываемая уравнением (рис 7.5):

(7.7)

Следует отметить, что персептрон Розенблатта можно использовать для решения весьма ограниченного класса задач, так как он может классифицировать только линейно разделимые входные сигналы.

Дельта-правило

Дельта-правило является математической моделью правил корректировки весов. Введем величину  , которая равна разности между требуемым   и реальным   выходом:

Тогда, веса персептрона после коррекции будут равны:

где:

 – номер текущей итерации обучения персептрона;

  – коэффициент скорости обучения, позволяет управлять средней величиной изменения весов;

 – величина входа соответствующая   синаптическому весу. Добавление величины   в произведение позволяет избежать изменение тех весов, которым на входе соответствовал ноль.

Существует доказательство сходимости этого алгоритма обучения персептрона за конечное число шагов.

23. Многослойный персептрон. Теорема о двуслойности персептрона

Многослойными персептронами называют нейронные сети прямого распространения. Входной сигнал в таких сетях распространяется в прямом направлении, от слоя к слою. Многослойный персептрон в общем представлении состоит из следующих элементов:

• множества входных узлов, которые образуют входной слой;

• одного или нескольких скрытых слоев вычислительных нейронов;

• одного выходного слоя нейронов.

Многослойный персептрон представляет собой обобщение однослойного персептрона Розенблатта. Примером многослойного персептрона является следующая модель нейронной сети:

Количество входных и выходных элементов в многослойном персептроне определяется условиями задачи. Сомнения могут возникнуть в отношении того, какие входные значения использовать, а какие нет. Вопрос о том, сколько использовать промежуточных слоев и элементов в них, пока совершенно неясен. В качестве начального приближения можно взять один промежуточный слой, а число элементов в нем положить равным полусумме числа входных и выходных элементов.

Многослойные персептроны успешно применяются для решения разнообразных сложных задач и имеют следующих три отличительных признака.

Свойство 1. Каждый нейрон сети имеет нелинейную функцию активации

Важно подчеркнуть, что такая нелинейная функция должна быть гладкой (т.е. всюду дифференцируемой), в отличие от жесткой пороговой функции, используемой в персептроне Розенблатта. Самой популярной формой функции, удовлетворяющей этому требованию, является сигмоидальная. Примером сигмоидальной функции может служить логистическая функция, задаваемая следующим выражением:

где   – параметр наклона сигмоидальной функции. Изменяя этот параметр, можно построить функции с различной крутизной.

Наличие нелинейности играет очень важную роль, так как в противном случае отображение «вход-выход» сети можно свести к обычному однослойному персептрону.

Свойство 2. Несколько скрытых слоев

Многослойный персептрон содержит один или несколько слоев скрытых нейронов, не являющихся частью входа или выхода сети. Эти нейроны позволяют сети обучаться решению сложных задач, последовательно извлекая наиболее важные признаки из входного образа.

Свойство 3. Высокая связность

Многослойный персептрон обладает высокой степенью связности, реализуемой посредством синаптических соединений. Изменение уровня связности сети требует изменения множества синаптических соединений или их весовых коэффициентов.

Комбинация всех этих свойств наряду со способностью к обучению на собственном опыте обеспечивает вычислительную мощность многослойного персептрона. Однако эти же качества являются причиной неполноты современных знаний о поведении такого рода сетей: распределенная форма нелинейности и высокая связность сети существенно усложняют теоретический анализ многослойного персептрона.

Теорема о двуслойности персептрона. Любой многослойный персептронможет быть представлен в виде двуслойного персептрона с необучаемыми весами первого слоя.

Доказательства не требует преводаватель.

24. Самоорганизующиеся карты Кохонена. Алгоритм обучения нс

Кохонена

Самоорганизующаяся карта Кохонена — соревновательная нейронная сеть с обучением без учителя, выполняющая задачу визуализации и кластеризации.

Состоит из 2х полносвязных слоёв. 2-ой слой гордо носит имя Кохонена.

Обучается методом последовательных приближений. На выходе смотрится, какой нейрон больше всего похож на образец. Этот нейрон называется «Победитель». Вокруг «Победителя» - область приближения. Сеть функционирует и обучается соответственно по следующему алгоритму:

1)инициализация. Весовым коэффициентам сети дают небольшие случайные значения.

2)новый входной сигнал

3)вычисление расстояния для всех нейронов в сети по формуле

4)определение победителя

5)настраивание нейрона-победителя и его окрестности , где r- скорость обучения

6)возврат на 2ой шаг.

Окрестность в конце обучения состоит только из победителя.

В общем виде алгоритм можно разбить на 3 части :

1) конкуренция

2) объединение

3) постройка весов

25. Самоорганизующиеся карты Кохонена. Квантование обучающего вектора.

/*это из файла с 3 лабой

Cамоорганизующаяся карта Кохонена – это однослойная нейронная сеть без смешения с конкурирующей функцией compet, имеющая определенную топологию размещения нейронов в N-мерном пространстве. В отличие от слоя Кохонена карта Кохонена после обучения поддерживает такое топологическое свойство, когда близким входным векторам соответствуют близко расположенные активные нейроны.

Первоначальная топология размещения нейронов в карте Кохонена формируется при создание карты с помощью функции newsom, одним из параметров которого является имя топологической функции gridtop, nextop или randtop, что соответствует размещению нейронов в узлах либо прямоугольной, либо гексагональной сетки, либо в узлах сетки со случайной топологией.

Расстояния между нейронами и векторами входов вычисляются с помощью следующих функций:

dist – евклидово расстояние d=sqrt((pos_i-p_j).^2);

boxdist – максимальное координатное смещение d=max(abs(pos_i-p_j));

mandist – расстояние суммарного координатного смещения d=sum(abs(pos_i-p_j));

linkdist – расстояние связи

Формирование саморганизующейся карты Кохонена осуществляется функцией

net=newsom(PR,[d₁, d₂,…],tfcn, dfсn, olr, osteps, tlr, tnd)), где Pr – массив размера R*2 минимальных значений векторов входа;

d₁, d₂…– число нейронов по i-й размерности карты. По умолчанию – двумерная карта с числом нейронов 5*8;

tfсn – функция топологии карты, по умолчанию nextop;

dfcn – функция расстояния, по умолчанию linkdist;

olr – параметр скорости обучения на этапе размещения, по умолчанию 0.9;

osteps – число циклов обучения на этапе подстройки, по умолчанию 1000;

tlr – параметр скорости на этапе подстройки, по умолчанию 0.02;

tnd – размер окрестности на этапе подстройки, по умолчанию 1.

Настройка карты Кохонена производится по каждому входному вектору независимо от того, применяется метод адаптации или метод обучения. В любом случае функция learnsom выполняет настройку карты нейронов.

Прежде всего определяется нейрон-победитель и корректируется его вектор весов и векторы соседних нейронов согласно соотношению

dw=lr*A2*(p′ – w),

где lr – параметр скорости обучения, равный olr для этапа упорядочения нейронов и tlr для этапа подстройки;

A2 – массив соседства для нейронов, расположенных в окрестности нейрона-победителя i:

Здесь а(i,q) – элемент выхода нейронной сети;

D(i,j) – расстояние между нейронами i и j;

nd – размер окрестности нейрона-победителя.

Таким образом, вес нейрона-победителя изменяется пропорционально половинному параметру скорости обучения, а веса соседних нейронов – пропорционально половинному значению этого параметра.

Весь процесс обучения карты Кохонена делится на два этапа:

А) этап упорядоченности векторов весовых коэффициентов в пространстве признаков;

Б) этап подстройки весов нейронов по отношению к набору векторов входа.

На этапе упорядочения используется фиксированное количество шагов. Начальный размер окрестности назначается равным максимальному расстоянию между нейронами для выбранной топологии и затем уменьшается до величины, используемой на следующем этапе, и вычисляется по следующей формуле:

nd=1.00001+(max(d)-1)(1-s/S),

где max(d) – максимальное расстояние между нейронами; s – номер текущего шага, а S – количество циклов на этапе упорядочения.

Параметр скорости обучения изменяется по правилу

lr =tlr+(olr-tlr)(1-s/S).

На этапе подстройки, который продолжается в течение оставшейся части процедуры обучения, размер окрестности остается постоянным и равным

nd=tnd+0.00001,

а параметр скорости обучения изменяется по следующему правилу

lr= tlr*S/s.

Параметр скорости обучения продолжает уменьшаться, но очень медленно. Малое значение окрестности и медленное уменьшение параметра скорости обучения хорошо настраивают сеть при сохранении размещения, найденного на предыдущем этапе. Число шагов на этапе подстройки должно значительно превышать число шагов на этапе размещения. На этом этапе происходит тонкая настройка весов нейронов по отношению к набору векторов входов.

Нейроны карты Кохонена будут упорядочиваться так, чтобы при равномерной плотности векторов входа нейроны также были распределены равномерно. Если векторы входа распределены неравномерно, то и нейроны будут иметь тенденцию распределяться в соответствии с плотностью размещения векторов входа.

Таким образом, при обучении карты Кохонена решается не только задачи кластеризации входных векторов, но и выполняется частичная классификация.

*/

/* это из инета

1.2Квантование обучающего вектора (Learning VectorQuantization)

Сеть была предложена Тойво Кохоненом в середине 80-х гг., позже, чем его работа по самоорганизованным картам. Сеть базируется на слое Кохонена, способному к сортировке примеров в соответствующие кластеры и используется как для проблем классификации, так и для кластеризации изображений.

Сеть содержит входной слой, самоорганизованную карту Кохонена и выходной слой. Пример сети изображен на рис. 6. Выходной слой имеет столько нейронов, сколько есть отличных категорий или классов. Карта Кохонена имеет ряд нейронов, сгруппированных для любого из этих классов, количество которых зависит от сложности отношения "вход-выход". Конечно, каждый класс будет иметь одинаковое количество элементов по всему слою. Слой Кохонена учится классификации с помощью обучающего множества. Сеть использует правила контролируемого обучения. Входной слой содержит столько нейронов, сколько имеется отдельных входных параметров.

Квантование обучающего вектора классифицирует свои входные данные в определенные группирования, то есть отображает n-измеримое пространство в m-измеримое пространство (берет n входов и создает m выходов). Карты сохраняют отношения между близкими соседями в обучающем множестве так, что входные образы, которые не было предварительно изучены, будут распределены по категориям их ближайших соседей в обучающих данных.

Рис. 6. Пример сети с квантованием обучающего вектора

В режиме обучения, контролируемая сеть использует слой Кохонена, где вычисляется расстояние от обучающего вектора до любого нейрона и ближайший нейрон объявляется победителем. Существует лишь один победитель на весь слой. Победителю разрешено возбуждать лишь один выходной нейрон, объявляя класс или кластер к которому принадлежит входной вектор. Если нейрон-победитель находится в ожидаемом классе обучающего вектора, его весы усиливаются в направлении обучающего вектора. Если нейрон-победитель не находится в классе обучающего вектора, весы соединений уменьшаются. Эта последняя операция упоминается как отталкивание (repulsion). Во время обучения отдельные нейроны, которые приписаны к частичному классу мигрируют к области, связанной с их специфическим классом.

Во время режима функционирования, вычисляется расстояние от входного вектора к любому нейрону и снова ближайший нейрон объявляется победителем. Это в свою очередь генерирует один выход, определяя частичный класс, найденный сетью.

Недостатки. Для сложной классификации похожих входных примеров, сеть требует большой карты Кохонена с большим количеством нейронов на класс. Это может быть преодолено целесообразным выбором обучающих примеров или расширением входного слоя.

Некоторые нейроны имеют тенденцию к победе слишком часто, то есть настраивают свои веса очень быстро, в то время как другие постоянно остаются незадействованными. Это часто случается, если их веса имеют значения далекие от обучающих примеров. Для устранения этого, нейрон, который побеждает слишком часто штрафуется, то есть уменьшаются весы его связей с каждым входным нейроном. Это уменьшения весов пропорционально к разности между частотой побед нейрона и частотой побед среднего нейрона.

Преимущества. Алгоритм предельной коррекции используется для усовершенствования решения даже если было найдено относительно хорошее решение. Алгоритм способен действовать, если нейрон-победитель находится в неправильном классе, а второй наилучший нейрон в правильном классе. Обучающий вектор должен быть близко от средней точки пространства, соединяющего эти два нейрона. Неправильный нейрон-победитель смещается из обучающего вектора, а нейрон из другого места продвигается к обучающему вектору. Эта процедура делает четкой границу между областями, где возможна неверная классификация.

В начале обучения желательно отключить отталкивание. Нейрон-победитель продвигается к обучающему вектору лишь тогда, когда обучающий вектор и нейрон-победитель находятся в одном классе. Такой подход целесообразен, если нейрон должен обойти область, имющую отличный класс для достижения необходимой области.

*/

25. Самоорганизующиеся карты Кохонена. Кластеризация

/*это из файла с 3 лабой

Cамоорганизующаяся карта Кохонена – это однослойная нейронная сеть без смешения с конкурирующей функцией compet, имеющая определенную топологию размещения нейронов в N-мерном пространстве. В отличие от слоя Кохонена карта Кохонена после обучения поддерживает такое топологическое свойство, когда близким входным векторам соответствуют близко расположенные активные нейроны.

Первоначальная топология размещения нейронов в карте Кохонена формируется при создание карты с помощью функции newsom, одним из параметров которого является имя топологической функции gridtop, nextop или randtop, что соответствует размещению нейронов в узлах либо прямоугольной, либо гексагональной сетки, либо в узлах сетки со случайной топологией.

Расстояния между нейронами и векторами входов вычисляются с помощью следующих функций:

dist – евклидово расстояние d=sqrt((pos_i-p_j).^2);

boxdist – максимальное координатное смещение d=max(abs(pos_i-p_j));

mandist – расстояние суммарного координатного смещения d=sum(abs(pos_i-p_j));

linkdist – расстояние связи

Формирование саморганизующейся карты Кохонена осуществляется функцией

net=newsom(PR,[d₁, d₂,…],tfcn, dfсn, olr, osteps, tlr, tnd)), где Pr – массив размера R*2 минимальных значений векторов входа;

d₁, d₂…– число нейронов по i-й размерности карты. По умолчанию – двумерная карта с числом нейронов 5*8;

tfсn – функция топологии карты, по умолчанию nextop;

dfcn – функция расстояния, по умолчанию linkdist;

olr – параметр скорости обучения на этапе размещения, по умолчанию 0.9;

osteps – число циклов обучения на этапе подстройки, по умолчанию 1000;

tlr – параметр скорости на этапе подстройки, по умолчанию 0.02;

tnd – размер окрестности на этапе подстройки, по умолчанию 1.

Настройка карты Кохонена производится по каждому входному вектору независимо от того, применяется метод адаптации или метод обучения. В любом случае функция learnsom выполняет настройку карты нейронов.

Прежде всего определяется нейрон-победитель и корректируется его вектор весов и векторы соседних нейронов согласно соотношению

dw=lr*A2*(p′ – w),

где lr – параметр скорости обучения, равный olr для этапа упорядочения нейронов и tlr для этапа подстройки;

A2 – массив соседства для нейронов, расположенных в окрестности нейрона-победителя i:

Здесь а(i,q) – элемент выхода нейронной сети;

D(i,j) – расстояние между нейронами i и j;

nd – размер окрестности нейрона-победителя.

Таким образом, вес нейрона-победителя изменяется пропорционально половинному параметру скорости обучения, а веса соседних нейронов – пропорционально половинному значению этого параметра.

Весь процесс обучения карты Кохонена делится на два этапа:

А) этап упорядоченности векторов весовых коэффициентов в пространстве признаков;

Б) этап подстройки весов нейронов по отношению к набору векторов входа.

На этапе упорядочения используется фиксированное количество шагов. Начальный размер окрестности назначается равным максимальному расстоянию между нейронами для выбранной топологии и затем уменьшается до величины, используемой на следующем этапе, и вычисляется по следующей формуле:

nd=1.00001+(max(d)-1)(1-s/S),

где max(d) – максимальное расстояние между нейронами; s – номер текущего шага, а S – количество циклов на этапе упорядочения.

Параметр скорости обучения изменяется по правилу

lr =tlr+(olr-tlr)(1-s/S).

На этапе подстройки, который продолжается в течение оставшейся части процедуры обучения, размер окрестности остается постоянным и равным

nd=tnd+0.00001,

а параметр скорости обучения изменяется по следующему правилу

lr= tlr*S/s.

Параметр скорости обучения продолжает уменьшаться, но очень медленно. Малое значение окрестности и медленное уменьшение параметра скорости обучения хорошо настраивают сеть при сохранении размещения, найденного на предыдущем этапе. Число шагов на этапе подстройки должно значительно превышать число шагов на этапе размещения. На этом этапе происходит тонкая настройка весов нейронов по отношению к набору векторов входов.

Нейроны карты Кохонена будут упорядочиваться так, чтобы при равномерной плотности векторов входа нейроны также были распределены равномерно. Если векторы входа распределены неравномерно, то и нейроны будут иметь тенденцию распределяться в соответствии с плотностью размещения векторов входа.

Таким образом, при обучении карты Кохонена решается не только задачи кластеризации входных векторов, но и выполняется частичная классификация.

*/

/* это из инета

Кластеризация

Наиболее распространенное применение сетей Кохонена - решение задачи классификации без учителя, т.е. кластеризации.

Напомним, что при такой постановке задачи нам дан набор объектов, каждому из которых сопоставлена строка таблицы (вектор значений признаков). Требуется разбить исходное множество на классы, т.е. для каждого объекта найти класс, к которому он принадлежит.

В результате получения новой информации о классах возможна коррекция существующих правил классификации объектов.

Вот два из распространенных применений карт Кохонена: разведочный анализ данных и обнаружение новых явлений [39].

Разведочный анализ данных. Сеть Кохонена способна распознавать кластеры в данных, а также устанавливать близость классов. Таким образом, пользователь может улучшить свое понимание структуры данных, чтобы затем уточнить нейросетевую модель. Если в данных распознаны классы, то их можно обозначить, после чего сеть сможет решать задачи классификации. Сети Кохонена можно использовать и в тех задачах классификации, где классы уже заданы, - тогда преимущество будет в том, что сеть сможет выявить сходство между различными классами.

Обнаружение новых явлений. Сеть Кохонена распознает кластеры в обучающих данных и относит все данные к тем или иным кластерам. Если после этого сеть встретится с набором данных, непохожим ни на один из известных образцов, то она не сможет классифицировать такой набор и тем самым выявит его новизну.

*/

25. Сеть Хопфилда. Архитектура, обучение

Сеть базируется на аналогии физики динамических систем. Начальные применения для этого вида сети включали ассоциативную, или адресованную по смыслу память и решали задачи оптимизации.

Сеть Хопфилда использует три слоя: входной, слой Хопфилда и выходной слой. Каждый слой имеет одинаковое количество нейронов. Входы слоя Хопфилда подсоединены к выходам соответствующих нейронов входного слоя через изменяющиеся веса соединений. Выходы слоя Хопфилда подсоединяются ко входам всех нейронов слоя Хопфилда, за исключением самого себя, а также к соответствующим элементам в выходном слое. В режиме функционирования, сеть направляет данные из входного слоя через фиксированные веса соединений к слою Хопфилда. Слой Хопфилда колебается, пока не будет завершено определенное количество циклов, и текущее состояние слоя передается на выходной слой. Это состояние отвечает образу, уже запрограммированному в сеть.

Обучение сети Хопфилда требует, чтобы обучающий образ был представлен на входном и выходном слоях одновременно. Рекурсивный характер слоя Хопфилда обеспечивает средства коррекции всех весов соединений. Недвоичная реализация сети должна иметь пороговый механизм в передаточной функции. Для правильного обучение сети соответствующие пары "вход-выход" должны отличаться между собой.

Если сеть Хопфилда используется как память, адресуемая по смыслу она имеет два главных ограничения. Во-первых, число образов, которые могут быть сохранены и точно воспроизведены является строго ограниченным. Если сохраняется слишком много параметров, сеть может сходится к новому несуществующему образу, отличному от всех запрограммированных образов, или не сходится вообще.

Граница емкости памяти для сети приблизительно 15% от числа нейронов в слое Хопфилда. Вторым ограничением парадигмы есть то, что слой Хопфилда может стать нестабильным, если обучающие примеры являются слишком похожими. Образец образа считается нестабильным, если он применяется за нулевое время и сеть сходится к некоторому другому образу из обучающего множества. Эта проблема может быть решена выбором обучающих примеров более ортогональных между собой.

Структурная схема сети Хопфилда:

Задача, решаемая данной сетью в качестве ассоциативной памяти, как правило, формулируется так. Известен некоторый образцовый набор двоичных сигналов (изображений, звуковых оцифровок, других данных, которые описывают определенные объекты или характеристики процессов). Сеть должна уметь с зашумленого сигнала, представленного на ее вход, выделить ("припомнить" по частичной информации) соответствующий образец или "дать вывод" о том, что входные данные не отвечают ни одному из образцов. В общем случае, любой сигнал может быть описан вектором x₁, х_і, х_n..., n - число нейронов в сети и величина входных и выходных векторов. Каждый элемент x_i равняется или +1, или -1. Обозначим вектор, который описывает k-ий образец, через X_k, а его компоненты, соответственно, - x_ik, k=0, ..., m-1, m - число образцов. Если сеть распознает (или "вспоминает") определенный образец на основе предъявленных ей данных, ее выходы будут содержать именно его, то есть Y = X_k, где Y - вектор выходных значений сети: y₁, y_i, y_n. В противном случае, выходной вектор не совпадет ни с одним образцом.

Если, например, сигналы представляют собой какое-то изображение, то, отобразив в графическом виде данные с выхода сети, можно будет увидеть картинку, которая целиком совпадает с одной из образцовых (в случае успеха) или же "свободную импровизацию" сети (в случае неудачи).

1.2.1Алгоритм функционирования сети

1. На стадии инициализации сети синаптические коэффициенты устанавливаются таким образом:

Здесь i и j - индексы, соответственно, предсинаптического и постсинаптического нейронов; xik, xjk - i-ый і j-ый элементы вектора k-ого образца.

2. На входы сети подается неизвестный сигнал. Его распространение непосредственно устанавливает значения выходов:

y_i(0) = x_i , i = 0...n-1,

поэтому обозначения на схеме сети входных сигналов в явном виде носит чисто условный характер. Нуль в скобке y_i означает нулевую итерацию в цикле работы сети.

3. Рассчитывается новое состояние нейронов

, j=0...n-1

и новые значения выходов

где f - передаточная функция в виде пороговой, приведена на рис. 10.

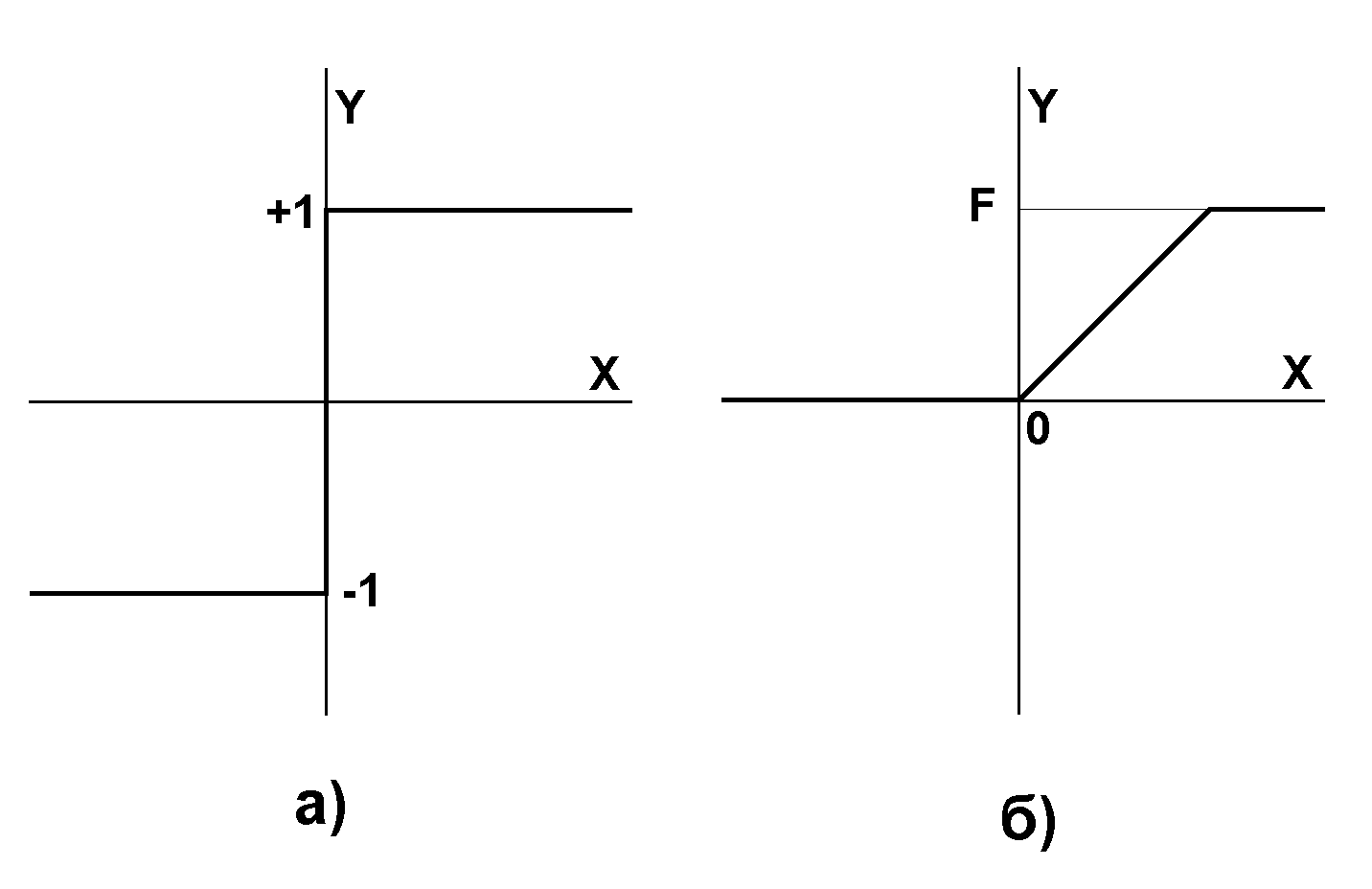
Рис. 10. Передаточные функции

4. Проверяем изменились ли выходные значения выходов за последнюю итерацию. Если да - переход к пункту 2, иначе (если выходы стабилизировались) - конец. При этом выходной вектор представляет собой образец, что лучше всего отвечает входным данным.

Иногда сеть не может провести распознавания и выдает на выходе несуществующий образ. Это связано с проблемой ограниченности возможностей сети. Для сети Хопфилда число запомненых образов m не должно превышать величины, приблизительно равной 0.15*n. Кроме того, если два образа А і Б сильно похожи, они, возможно, будут вызвать в сети перекрестные ассоциации, то есть предъявление на входы сети вектора А приведет к появлению на ее выходах вектора Б и наоборот. Благодаря итерационному алгоритму, машина продвигается к наилучшему решению

1.2.2Архитектура сети

Схема сети Хопфилда с тремя нейронами

Нейронная сеть Хопфилда состоит из искусственных нейронов. Каждый нейрон системы может принимать одно из двух состояний (что аналогично выходу нейрона с пороговой функцией активации):

Из-за их биполярной природы нейроны сети Хопфилда иногда называют спинами.

Взаимодействие спинов сети описывается выражением:

где — элемент матрицы взаимодействий , которая состоит из весовых коэффициентов связей между нейронами. В эту матрицу в процессе обучения записывается М «образов» — N-мерных бинарных векторов:

В сети Хопфилда матрица связей является симметричной ( ), а диагональные элементы матрицы полагаются равными нулю ( ), что исключает эффект воздействия нейрона на самого себя и является необходимым для сети Хопфилда, но не достаточным условием, устойчивости в процессе работы сети. Достаточным является асинхронный режим работы сети. Подобные свойства определяют тесную связь с реальными физическими веществами, называемыми спиновыми стёклами.

1.2.3Обучение сети

Алгоритм обучения сети Хопфилда существенно отличается от таких классических алгоритмов обучения перцептронов, как метод коррекции ошибки или метод обратного распространения ошибки. Отличие заключается в том, что вместо последовательного приближения к нужному состоянию с вычислением ошибок, все коэффициенты матрицы рассчитываются по одной формуле, за один цикл, после чего сеть сразу готова к работе. Вычисление коэффициентов основано на следующем правиле: для всех запомненных образов матрица связи должна удовлетворять уравнению

поскольку именно при этом условии состояния сети будут устойчивы — попав в такое состояние, сеть в нём и останется.

Некоторые авторы относят сеть Хопфилда к обучению без учителя. Но это неверно, так как обучение без учителя предполагает отсутствие информации о том, к каким классам нужно относить стимулы. Для сети Хопфилда без этой информации нельзя настроить весовые коэффициенты, поэтому здесь можно говорить лишь о том, что такую сеть можно отнести к классу оптимизирующих сетей (фильтров). Отличительной особенностью фильтров является то, что матрица весовых коэффициентов настраивается детерминированным алгоритмом раз и навсегда, и затем весовые коэффициенты больше не изменяются. Это может быть удобно для физического воплощения такого устройства, так как на схемотехническом уровне реализовать устройство с переменными весовыми коэффициентами на порядок сложнее. Примером фильтра без обратных связей может служить алгоритм CC4 (Cornel classification), автором которого является S.Kak.

В сети Хопфилда есть обратные связи и поэтому нужно решать проблему устойчивости. Веса между нейронами в сети Хопфилда могут рассматриваться в виде матрицы взаимодействий . В работе Cohen, Grossberg^[1] показано, что сеть с обратными связями является устойчивой, если её матрица симметрична и имеет нули на главной диагонали. Имеется много устойчивых систем, например, все сети прямого распространения, а также современные рекуррентные сети Джордана и Элмана, для которых не обязательно выполнять условие на симметрию. Но это происходит вследствие того, что на обратные связи наложены другие ограничения. В случае сети Хопфилда условие симметричности является необходимым, но не достаточным, в том смысле, что на достижение устойчивого состояния влияет ещё и режим работы сети. Ниже будет показано, что только асинхронный режим работы сети гарантирует достижение устойчивого состояния сети, в синхронном случае возможно бесконечное переключение между двумя разными состояниями (такая ситуация называется динамическим аттрактором, в то время как устойчивое состояние принято называть статическим аттрактором).

Запоминаемые векторы должны иметь бинарный вид. После этого происходит расчёт весовых коэффициентов по следующей формуле:

где — размерность векторов, — число запоминаемых выходных векторов, — номер запоминаемого выходного вектора, — i-я компонента запоминаемого выходного j-го вектора.

Это выражение может стать более ясным, если заметить, что весовая матрица может быть найдена вычислением внешнего произведения каждого запоминаемого вектора с самим собой и суммированием матриц, полученных таким образом. Это может быть записано в виде

где — i-й запоминаемый вектор-строка.

Расчёт этих весовых коэффициентов и называется обучением сети.

Как только веса заданы, сеть может быть использована для получения запомненного выходного вектора по данному входному вектору, который может быть частично неправильным или неполным. Для этого выходам сети сначала придают значения этого начального вектора. Затем сеть последовательно меняет свои состояния согласно формуле:

где — активационная функция, и — текущее и следующее состояния сети, до тех пор, пока состояния и не совпадут (или, в случае синхронного режима работы, не совпадут состояния с и одновременно с ). Именно этот процесс называется конвергенцией сети. Полученное устойчивое состояние (статический аттрактор), или, возможно, в синхронном случае пара { } (динамический аттрактор), является ответом сети на данный входной образ.

28. Сеть Хемминга. Архитектура, обучение

Сеть Хемминга (Hamming) - расширение сети Хопфилда. Сеть Хемминга реализует классификатор, базирующийся на наименьшей погрешности для векторов двоичных входов, где погрешность определяется расстоянием Хемминга. Расстояние Хемминга определяется как число бит, отличающихся между двумя соответствующими входными векторами фиксированной длины. Один входной вектор является незашумленым примером образа, другой - испорченным образом. Вектор выходов обучающего множества является вектором классов, к которым принадлежат образы. В режиме обучения входные векторы распределяются по категориям, для которых расстояние между образцовыми входными векторами и текущим входным вектором является минимальным.

Сеть Хемминга имеет три слоя: входной слой с количеством узлов, сколько имеется отдельных двоичных признаков; слой категорий (слой Хопфилда), с количеством узлов, сколько имеется категорий или классов; выходной слой, который отвечает числу узлов в слое категорий.

Сеть есть простой архитектурой прямого распространения с входным уровнем, полностью подсоединенным к слою категорий. Каждый элемент обработки в слое категорий является обратно подсоединенным к каждому нейрону в том же самом слое и прямо подсоединенным к выходному нейрону. Выход из слоя категорий к выходному слою формируется через конкуренцию.

Обучение сети Хемминга похоже на методологию Хопфилда. На входной слой поступает желаемый обучающий образ, а на выход выходного слоя поступает значение желаемого класса, к которому принадлежит вектор. Выход содержит лишь значение класса к которому принадлежит входной вектор. Рекурсивный характер слоя Хопфилда обеспечивает средства коррекции всех весов соединений.

Структурная схема сети Хемминга

1.2.4Алгоритм функционирования сети Хемминга

1. На стадии инициализации весовым коэффициентам первой слоя и порогу передаточной функции присваиваются такие значения:

W_ik=x_I^k/2, i=0...n-1, k=0...m-1

b_k = n / 2, k = 0...m-1

Здесь x_i^k - i-ый элемент k-ого образца.

Весовые коэффициенты тормозящих синапсов в втором слое берут равными некоторой величине 0 < v < 1/m. Синапс нейрона, связанный с его же выходом имеет вес +1.

2. На входы сети подается неизвестный вектор x₁, x_i, x_n ... Рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя):

, j=0...m-1

После этого получения значения инициализируют значения выходов второго слоя:

y_j⁽²⁾ = y_j⁽¹⁾, j = 0...m-1

3. Вычисляются новые состояния нейронов второго слоя:

и значения их выходов:

Передаточная функция f имеет вид порога, причем величина b должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению.

4. Проверяется, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если да - перейти к шагу 3. Иначе - конец.

Роль первой слоя является условной: воспользовавшись один раз на первом шаге значениями его весовых коэффициентов, сеть больше не возвращается к нему, поэтому первый слой может быть вообще исключен из сети.

Сеть Хемминга имеет ряд преимуществ над сетью Хопфилда. Она способна найти минимальную погрешность, если погрешности входных бит являются случайными и независимыми. Для функционирования сети Хемминга нужно меньшее количество нейронов, поскольку средний слой требует лишь один нейрон на класс, вместо нейрона на каждый входной узел. И, в конце концов, сеть Хемминга не страдает от неправильных классификаций, которые могут случиться в сети Хопфилда. В целом, сеть Хемминга быстрее и точнее, чем сеть Хопфилда.

29. Rbf сети. Архитектура. Применимость.

Сеть радиальных базисных функций - нейронная сеть прямого распространения сигнала, которая содержит промежуточный (скрытый) слой радиально симметричных нейронов. Такой нейрон преобразовывает расстояние от данного входного вектора до соответствующего ему "центра" по некоторому нелинейному закону (обычно функция Гаусса)

Сети, использующие радиальные базисные функции (RBF-сети), являются частным случаем двухслойной сети прямого распространения. Каждый элемент скрытого слоя использует в качестве активационной функции радиальную базисную функцию типа гауссовой. Радиальная базисная функция (функция ядра) центрируется в точке, которая определяется весовым вектором, связанным с нейроном. Как позиция, так и ширина функции ядра должны быть обучены по выборочным образцам. Обычно ядер гораздо меньше, чем обучающих примеров. Каждый выходной элемент вычисляет линейную комбинацию этих радиальных базисных функций. С точки зрения задачи аппроксимации скрытые элементы формируют совокупность функций, которые образуют базисную систему для представления входных примеров в построенном на ней пространстве.

Существуют различные алгоритмы обучения RBF-сетей. Основной алгоритм использует двушаговую стратегию обучения, или смешанное обучение. Он оценивает позицию и ширину ядра с использованием алгоритма кластеризации "без учителя", а затем алгоритм минимизации среднеквадратической ошибки "с учителем" для определения весов связей между скрытым и выходным слоями. Поскольку выходные элементы линейны, применяется неитерационный алгоритм. После получения этого начального приближения используется градиентный спуск для уточнения параметров сети.

Этот смешанный алгоритм обучения RBF-сети сходится гораздо быстрее, чем алгоритм обратного распространения для обучения многослойных перцептронов. Однако RBF-сеть часто содержит слишком большое число скрытых элементов. Это влечет более медленное функционирование RBF-сети, чем многослойного перцептрона. Эффективность (ошибка в зависимости от размера сети) RBF-сети и многослойного перцептрона зависят от решаемой задачи.

Радиально-симметричные функции – простейший класс функций. В принципе, они могут быть использованы в разных моделях (линейных и нелинейных) и в разных сетях (многослойных и однослойных). Традиционно термин RBF сети ассоциируется с радиально-симметричными функциями в однослойных сетях, имеющих структуру, представленную на рисунке 2.

То есть, каждый из n компонентов входного вектора подается на вход m базисных функций и их выходы линейно суммируются с весами:

Структура RBF сети.

Таким образом, выход RBF сети является линейной комбинацией некоторого набора базисных функций: (5)

Применимость

RBF-сети широко применяются обработки сигналов и прогнозирования временных зависимостей: прогнозирование финансовых показателей и надежности электродвигателей и систем электропитания на самолетах; предсказание мощности АЭС; обработка траекторных измерений. При решении этих задач в настоящее время все чаще переходят от простейших регрессионных и других статистических моделей прогноза к существенно нелинейным адаптивным экстраполирующим фильтрам, реализованным в виде сложных нейронных сетей.

Нейросетевые методы обработки гидролокационных сигналов применяются с целью распознавания типа надводной или подводной цели, определения координат цели. Структура сейсмических сигналов весьма близка к структуре гидролокационных сигналов. Их обработка нейросетью или нейрокомпьютером с достаточной точностью позволяет получить данные о координатах и мощности землетрясения или ядерного взрыва.

29. Rbf сети. Алгоритм обучения. Расчет опорных точек, параметра рассеяния и выходной весовой матрицы

Сеть радиальных базисных функций - нейронная сеть прямого распространения сигнала, которая содержит промежуточный (скрытый) слой радиально симметричных нейронов. Такой нейрон преобразовывает расстояние от данного входного вектора до соответствующего ему "центра" по некоторому нелинейному закону (обычно функция Гаусса)

Сети, использующие радиальные базисные функции (RBF-сети), являются частным случаем двухслойной сети прямого распространения. Каждый элемент скрытого слоя использует в качестве активационной функции радиальную базисную функцию типа гауссовой. Радиальная базисная функция (функция ядра) центрируется в точке, которая определяется весовым вектором, связанным с нейроном. Как позиция, так и ширина функции ядра должны быть обучены по выборочным образцам. Обычно ядер гораздо меньше, чем обучающих примеров. Каждый выходной элемент вычисляет линейную комбинацию этих радиальных базисных функций. С точки зрения задачи аппроксимации скрытые элементы формируют совокупность функций, которые образуют базисную систему для представления входных примеров в построенном на ней пространстве.

Существуют различные алгоритмы обучения RBF-сетей. Основной алгоритм использует двушаговую стратегию обучения, или смешанное обучение. Он оценивает позицию и ширину ядра с использованием алгоритма кластеризации "без учителя", а затем алгоритм минимизации среднеквадратической ошибки "с учителем" для определения весов связей между скрытым и выходным слоями. Поскольку выходные элементы линейны, применяется неитерационный алгоритм. После получения этого начального приближения используется градиентный спуск для уточнения параметров сети.

Этот смешанный алгоритм обучения RBF-сети сходится гораздо быстрее, чем алгоритм обратного распространения для обучения многослойных перцептронов. Однако RBF-сеть часто содержит слишком большое число скрытых элементов. Это влечет более медленное функционирование RBF-сети, чем многослойного перцептрона. Эффективность (ошибка в зависимости от размера сети) RBF-сети и многослойного перцептрона зависят от решаемой задачи.

Алгоритм обучение сети RBF

1. Выбрать размер скрытого шара равным количеству тренировочных шаблонов . Синаптические веса нейронов скрытого шара принять равными 1.

2. Разместить центры активационных функций нейронов скрытого шара в точках пространства входных сигналов сети, которые входят в набор тренировочных шаблонов .

3. Выбрать ширины окон активационных функций нейронов скрытого шара , достаточно большими, но так, чтобы они не накладывались одна на другую в пространстве входных сигналов сети.

4. Определить весы нейронов исходного шара сети . Для этого предъявить сети весь набор тренировочных шаблонов. Выход -го нейрона исходного шара для -го шаблона будет равный:

Расписав это уравнение для всех выходов сети и всех шаблонов, получим следующее уравнение в матричной форме: ,

где - интерполяционная матрица, ;

- матрица исходных синаптических весов;

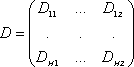- матрица исходных шаблонов.

Решение дает нам искомые значения исходных синаптических весов, что обеспечивает прохождения интерполяционной поверхности через тренировочные шаблоны в пространстве входных образов.

Опорные точки задают точки, через которые должна пройти аппроксимирующая функция. В простейшем случае, как было отмечено выше, можно использовать все образы обучающей последовательности для формирования опорных точек и соответственно для определения нейронов скрытого слоя. Однако это сопряжено со значительными затратами. Для их снижения часто в качестве центров RBF- и HBF-сетей используется подмножество обучающей последовательности. При этом иногда предусматривается незначительная модификация входных образов и весов соединений («шум»). Подобный «шум» необходим, например, в тех случаях, когда число k скрытых нейронов превышает число N образов обучающей последовательности. До сих пор мы обычно предполагали, что k ≤ N. Принципиально, способ применим и в случае когда k > N.

Для наиболее целесообразного использования данных обучающей последовательности в RBF-сетях следует принять во внимание, что различия между некоторыми векторами обучающей последовательности могут быть малы или незначительны. Для выявления таких векторов могут быть использованы различные методы автоматической классификации или кластер-анализа. Они позволяют выявить кластеры (группы) подобных (близких) векторов и представить эти кластеры лишь одним вектором (прототипом, стереотипом, типичным представителем). Достигаемое при этом значительное сокращение (сжатие) данных – весьма существенное достоинство RBF-сетей. В настоящее время разработано большое количество алгоритмов автоматической классификации или кластеризации. Рассмотрим один из примеров простых алгоритмов кластеризации на основе следующей стратегии (ab – hoc – Methode) выявления кластеров. Выбирается произвольно 1-й элемент обучающей последовательности. Он объявляется в качестве прототипа (стереотипа) 1-го кластера. Затем все векторы обучающей последовательности, расстояния до которых от выбранного вектора не превышает некоторого порога, включаются в 1-й кластер.

При появлении вектора обучающей последовательности, который не может быть включен в первый кластер, он объявляется прототипом (стереотипом) 2-го кластера. Процедура далее повторяется с оставшимися образами обучающей последовательности до тех пор, пока все ее образы не будут разделены на кластеры.

Выбор параметра рассеяния σ.

Параметр σ определяет рассеяние вокруг опорной точки Ui. Путем комбинации опорных точек и параметров σi необходимо по возможности «покрыть» все пространство образов. Наряду с выбором достаточного числа опорных точек, которые должны быть по возможности равномерно распределены по пространству образов, подходящий выбор значений параметров σi служит заполнению возможных пустот.

В практических приложениях обычно применяется метод k ближайших соседей (k – nearest – neighbor – Method) для определения k ближайших соседей вокруг точки Ui. После этого определяется средний вектор U'i. Расстояние между Ui и U'i служит затем мерой для выбора значения параметра σi. Для многих приложений рабочим правилом является выбор σ = 1 (default – установка).

Другой подход к определению оптимального множества центральных векторов для RBF-сетей может быть основан на использовании самоорганизующихся карт (сети Кохонена). Для этого в большинстве случаев образы обучающей последовательности предварительно нормируются по длине, равной 1. После этого выбирается случайно k из N образов обучающей последовательности в качестве начальных (стартовых) значений центральных векторов и определяется скалярное произведение xi'wj между вектором xi обучающей последовательности и каждым из k центральных векторов wj, где j = 1, 2, ..., k. Это скалярное произведение является мерой подобия (сходства) обоих векторов, нормированных по длине, равной 1. При этом тот центральный вектор wj, расстояние от которого до текущего вектора обучающей последовательности минимально (или: для которого указанное скалярное произведение максимально), объявляется «победителем». Затем он сдвигается на небольшую величину в направлении текущего вектора xi обучающей последовательности:

Здесь α - коэффициент коррекции. Эта процедура многократно повторяется по всем образам обучающей последовательности.

Дополнительное преимущество применения самоорганизующихся карт (self – organizing maps) состоит в том, что в них учитывается и близость между нейронами скрытого слоя. В силу этого модифицируется не только нейрон – «победитель», но и нейроны в окрестности вокруг него (однако в существенно меньшей степени).

Расчет выходной весовой матрицы c.

После определения опорных точек Ui и параметров рассеяния σi необходимо рассчитать весовую матрицу c. Обучающая последовательность T содержит векторы Vi = (xi, yi ), где xi – i- й образ обучающей последовательности, а yi – значение функции для него. Часть этих векторов Vi уже была использована для определения опорных точек Ui. Для определения матрицы c целесообразно использовать алгоритм типа Backpropagation. Для этого вектор xi обучающей последовательности подается на вход сети, затем рассчитываются активации нейронов скрытого слоя h(xi). Выход нейронов скрытого слоя представим в виде вектора h. Этот вектор h «пропускается» через весовую матрицу

где сij – вес связи нейрона i скрытого слоя и нейрона j выходного слоя. В результате получается действительный выходной вектор f, который сравнивается с требуемым выходным вектором y. На основе сравнения этих векторов и осуществляется коррекция весовой матрицы c (подобно алгоритму Backpropagation).

31. Rbf сети. Аппроксимация

Сеть радиальных базисных функций - нейронная сеть прямого распространения сигнала, которая содержит промежуточный (скрытый) слой радиально симметричных нейронов. Такой нейрон преобразовывает расстояние от данного входного вектора до соответствующего ему "центра" по некоторому нелинейному закону (обычно функция Гаусса)

Сети, использующие радиальные базисные функции (RBF-сети), являются частным случаем двухслойной сети прямого распространения. Каждый элемент скрытого слоя использует в качестве активационной функции радиальную базисную функцию типа гауссовой. Радиальная базисная функция (функция ядра) центрируется в точке, которая определяется весовым вектором, связанным с нейроном. Как позиция, так и ширина функции ядра должны быть обучены по выборочным образцам. Обычно ядер гораздо меньше, чем обучающих примеров. Каждый выходной элемент вычисляет линейную комбинацию этих радиальных базисных функций. С точки зрения задачи аппроксимации скрытые элементы формируют совокупность функций, которые образуют базисную систему для представления входных примеров в построенном на ней пространстве.

Существуют различные алгоритмы обучения RBF-сетей. Основной алгоритм использует двушаговую стратегию обучения, или смешанное обучение. Он оценивает позицию и ширину ядра с использованием алгоритма кластеризации "без учителя", а затем алгоритм минимизации среднеквадратической ошибки "с учителем" для определения весов связей между скрытым и выходным слоями. Поскольку выходные элементы линейны, применяется неитерационный алгоритм. После получения этого начального приближения используется градиентный спуск для уточнения параметров сети.

Этот смешанный алгоритм обучения RBF-сети сходится гораздо быстрее, чем алгоритм обратного распространения для обучения многослойных перцептронов. Однако RBF-сеть часто содержит слишком большое число скрытых элементов. Это влечет более медленное функционирование RBF-сети, чем многослойного перцептрона. Эффективность (ошибка в зависимости от размера сети) RBF-сети и многослойного перцептрона зависят от решаемой задачи.

При аппроксимации при помощи центральных функций независимо от числа N образов обучающей последовательности выбирается число k центров или k скрытых нейронов. Для этого в частности можно использовать соответствующее подмножество образов обучающей последовательности или другие опорные точки, предварительно определенные тем или иным способом. В силу этого эти центры теперь обозначаются не через xj, а иначе. Для их обозначения используются векторы tj (от teacher) или чаще Wj. Объяснение для этого в том, что координаты опорных точек почти во всех реализациях запоминаются в виде весов wij нейросети. В этом случае в частности лучше проявляется сходство с другими алгоритмами обучения.

На рисунке приведена структура обобщенной RBF-сети, содержащей один скрытый слой с фиксированным числом k нейронов. Данные опорных точек запоминаются в виде весов wij скрытых нейронов.

Для k различных центров аппроксимирующая функция f принимает следующий вид:

Для определения k коэффициентов с1, с2, ..., сk имеется N уравнений. При этом можно использовать условия интерполяции для всех N образов обучающей последовательности.

Обозначим , тогда проблему интерполяции можно представить так:

В случае N > k эта система переопределена и не имеет точного решения (интерполяция). Путем аппроксимации можно минимизировать сумму квадратов ошибок по всем образам обучающей последовательности. Это приведет к следующему решению: ,

где H+ - псевдоинверсная матрица Мура – Пенроза («Moore – Penrose Pseudoinverse») относительно матрицы H:

В соответствии с теоремой Микчелли (Micchelli) инверсная матрица существует в тех случаях, когда производная h' центральной функции монотонна, а в качестве центров wj используется подмножество образов xj обучающей последовательности.

31. Ассоциативная сеть. Сжатие информации

АсС – интеллектуальная система накопления и использования знаний.

Форма представления и обработки знаний даёт следующие возможности:

1. накопление знаний

в результате прямого обучения;

в результате алгоритмизации своего опыта.

2. использование знаний

создание алгоритмов и программ для достижения поставленной цели;

интеллектуальный поиск нужной информации;

Прямое обучение – задание программы достижения цели на языке программирования. Удобнее использовать специальный язык, но теоретически возможно сделать перевод во внутреннее представление с любого из существующих языков программирования.

Алгоритмизация своего опыта – использование средств логического вывода для достижения такой цели, для которой нет готовой программы. Эти средства позволяют:

- трансформировать имеющиеся алгоритмы;

- создавать новые алгоритмы на основе анализа имеющихся знаний и создания гипотез, для подтверждения их на опыте (частный случай – вопрос программисту).

Средствами системы возможно решение таких задач, как:

- генерация (созданных системой) программ обработки данных на любом из существующих языков программирования;

- машинный перевод высокого качества;

- создание глобальной сети знаний на базе Интернет.

Перевод с естественного языка на другой естественный язык осуществляется через объектную модель описываемой в тексте ситуации. Это даёт практически неограниченные возможности для приближения качества машинного перевода к человеческому.

Двунаправленная ассоциативная память (ДАП) является гетероассоциативной; входной вектор поступает на один набор нейронов, а соответствующий выходной вектор появляется на другом наборе нейронов. Как и сеть Хопфилда, ДАП способна к обобщению, вырабатывая правильные реакции, несмотря на искаженные входы. Кроме того, могут быть реализованы адаптивные версии ДАП, выделяющие эталонный образ из зашумленных экземпляров. Эти возможности сильно напоминают процесс мышления человека и позволяют искусственным нейронным сетям приблизиться к моделированию естественного мозга.

Структура дап

На рис. 10.1 приведена базовая конфигурация ДАП. Она выбрана таким образом, чтобы подчеркнуть сходство с сетями Хопфилда и предусмотреть увеличения количества слоев. На рис. 10.1 входной вектор   обрабатывается матрицей весов  сети, в результате чего вырабатывается вектор выходных сигналов нейронов  . Вектор   затем обрабатывается транспонированной матрицей   весов сети, которая вырабатывает новые выходные сигналы, представляющие собой новый входной вектор  . Процесс повторяется до тех пор, пока сеть не достигнет стабильного состояния, в котором ни вектор  , ни вектор   не изменяются. Заметим, что нейроны в слоях 1 и 2 функционируют, как и в других парадигмах, вычисляя сумму взвешенных входов и вычисляя по ней значение функции активации  . Этот процесс может быть выражен следующим образом:

или в векторной форме:

,

где   — вектор выходных сигналов нейронов слоя 2,   — вектор выходных сигналов нейронов слоя 1,   — матрица весов связей между слоями 1 и 2,   — функция активации.

Рис. 10.1. 

Аналогично,

,

где   является транспозицией матрицы  .

Как отмечено нами ранее, Гроссберг показал преимущества использования сигмоидальной (логистической) функции активации

где   — выход нейрона  ,   — взвешенная сумма входных сигналов нейрона  ,   — константа, определяющая степень кривизны.

В простейших версиях ДАП значение константы   выбирается большим, в результате чего функция активации приближается к простой пороговой функции. В дальнейшем будем предполагать, что используется пороговая функция активации.

Примем также, что существует память внутри каждого нейрона в слоях 1 и 2 и что выходные сигналы нейронов изменяются одновременно с каждым тактом синхронизации, оставаясь постоянными в паузах между этими тактами. Таким образом, поведение нейронов может быть описано следующими правилами:

где   представляет собой величину выходного сигнала нейрона   в момент времени  .

Заметим, что, как и в описанных ранее сетях, слой 0 не производит вычислений и не имеет памяти ; он является только средством распределения выходных сигналов слоя 2 к элементам матрицы  .