3. Законы распределения и числовые характеристики непрерывных случайных величин Числовые характеристики непрерывных св

Функция распределения или плотность распределения полностью определяет непрерывную СВ. Однако, СВ может быть задана также несколькими числовыми характеристиками, к которым относятся, прежде всего, математическое ожидание (МО) и дисперсия.

МО или средним значением непрерывной СВ X называется число, определяемое по формуле:

Дисперсией непрерывной СВX называется математическое ожидание квадрата её отклонения от среднего значения:

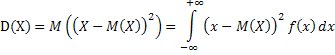
Арифметическое значение корня квадратного из дисперсии называется средним квадратическим отклонением (СКО):

Свойства МО:

1. МО суммы СВ равно сумме их математических ожиданий:

2. МО произведения независимых (вероятность появления одной, не влияет на вероятность появления другой величины) СВ равно произведению их МО:

3.СКО среднего арифметического для n одинаково распределённых и взаимно независимых случайных величин в корень из n раз ( ) меньше СКО для каждой случайной величины:

Свойства дисперсии:

1. Дисперсия постоянной величины равна 0.

2. Дисперсия сумм (или разности) двух независимыхСВ равна сумме их дисперсий:

Распределения непрерывных случайных величин.

Наиболее распространённымиявляются распространенными непрерывных СВ равномерное, показательное (экспоненциальное), нормальное, усеченное нормальное.

а) Равномерное распределение:

Непрерывное СВX принимающая значения (a;b) имеет равномерное распределение, если плотность распределения имеет вид:

0

a

b

x

Функция распределения СВX имеет вид:

0

a

b

x

Числовые характеристики СВ Х равномерно распределенной в интервале (a;b) имеют следующие значения:

б) Показательное распределение:

Непрерывная СВX принимающая неотрицательные значения в интервале (0; +∞) имеет показательное распределение, если плотность распределения имеет вид:

где –параметр распределения.

Функция распределения в этом случае имеет вид:

Числовые характеристики показательного распределения определяются по следующим формулам:

в) Нормальное распределение

Нормальным называют распределение СВ Х, которое имеет плотность

– математическое ожидание

– СКО

Функция распределения в этом случае определяется по следующей формуле:

Введём в рассмотрение нормированную и центрированную случайную величину с нормальным распределением:

СВ наз-ся центрированной, если её СО равна 0.

СВ наз-ся нормированной, если её СКО (и дисперсия) равна 1.

Для неё составлена табличная функция Лапласа, имеющая вид:

С помощью табличной функции Лапласа можно определить вероятность попадания СВ Х в заданный интервал ( ; ):

Часто требуется вычислить вероятность того, что отклонение нормально распределенной СВ Х от её МО по абсолютной величине меньше заданного числа , т.е. требуется найти:

Заменим неравенство с модулем равносильным ему двойным неравенством.

Тогда по формуле (*) получим:

Т.к. функция Лапласа нечетная.