Теорема Шеннона о кодировании для дискретного канала без помех

Если источник информации имеет энтропию H(z) единиц информации на символ сообщения, а канал связи обладает пропускной способностью С единиц информации в единицу времени, то:

1) сообщения, вырабатываемые источником, всегда можно закодировать так, чтобы скорость υ_z их передачи была сколь угодно близка к υ_zmax=С/H(z)

2) не существует метода кодирования, позволяющего сделать эту скорость большей, чем υ_zmax.

Согласно сформулированной теореме существует метод кодирования, позволяющий при υ_z* H(z) ≤ С передавать всю информацию, вырабатываемую источником. Теорема лишь утверждает о возможности экономного (эффективного) кодирования, но не дает метода такого кодирования. Первым эффективным кодом был код Шеннона-Фэно, в 1952 году Хаффман предложил свой алгоритм эффективного кодирования. В настоящее время разработано достаточно большое количество алгоритмов сжатия и их программных и аппаратных реализаций.

Пропускная способность канала.

Важнейшей характеристикой канала являетсяся его пропускная способность С, которая определяется как наибольшая возможная скорость передачи информаци по данному каналу

С= υ_x*max{I(y,x)},

где υ_x- предельная скорость передачи по каналу элементарных сигналов;

max{I(y,x)} – max возможное значение среднего количества информации, содержащееся в одном символе принятого сигнала.

Количество информации I(y,x), переносимое одним символом, равно уменьшению степени неопределённости нашего знания о передаваемом сигнале в результате приёма. Неопределённость не устраняется полностью, так как принятый сигнал может оказаться искажённым помехой,

т.е. I(y,x)=H(x)-H(y/x),

где H(x)-энтропия источников сигналов, характеризующая среднюю неопределённость передаваемого сигнала до приёма;

H(y/x) – средняя условная энтропия ансамбля сигналов х при известных, принятых сигналах у.

Так как ищется max{I(y,x)}, эта величина не зависит от конкретного источника, поэтому пропускная способность зависит исключительно от вида канала.

11. Модуляция сигналов с использованием гармонической несущей. Спектры модулированных сигналов.

Основным видом несущих сигналов являются гармонические колебания:

u(t) = Ucos(t+),

которые имеют три свободных параметра: U,  и . В зависимости от того, на какой из данных параметров переносится информация, различают амплитудную (АМ), частотную (ЧМ) или фазовую (ФМ) модуляцию несущего сигнала. Частотная и фазовая модуляция взаимосвязаны, поскольку изменяют аргумент функции косинуса, и их обычно объединяют под общим названием - угловая модуляция (angle modulation). В каналах передачи цифровой информации получила также распространение квадратурная модуляция, при которой одновременно изменяются амплитуда и фаза несущих колебаний.

При использовании в качестве несущих сигналов периодических последовательностей импульсов свободными параметрами модуляции могут быть амплитуда, длительность, частота следования импульсов и фаза (положение импульса относительно определенной точки тактового интервала). Это дает четыре основных вида импульсной модуляции: АИМ, ДИМ, ЧИМ и ФИМ.

В качестве несущих сигналов можно использовать не только периодические колебания, но и стационарные случайные процессы. В качестве модулируемых параметров случайных сигналов используются моменты случайных процессов. Так, например, модуляция второго момента случайных последовательностей (модуляция по мощности) представляет собой аналогию амплитудной модуляции.

Определим спектр простейшего непериодического сигнала – прямоугольного импульса. Электрический импульс – это напряжение или ток, действующие в течение короткого промежутка времени, называемого длительностью импульса. Для удобства анализа частотных свойств импульсов их обычно идеализируют, считая совпадающими по форме с простыми геометрическими фигурами: прямоугольный, трапециидальный, треугольный, пилообразный и т.д.

Наиболее часто в вычислительной технике для передачи данных используется прямоугольный импульс, внешний вид и основные параметры которого приведены на рис. 6.

Рис. 6. Прямоугольный импульс

Аналитически во временном представлении импульс описывается функцией

Для определения спектра этого импульса подставим его аналитическое описание в формулу спектра непериодического сигнала:

Воспользовавшись формулой Эйлера

получим .

Иногда в радиотехнической литературе это выражение записывают так

.

Модуль этой функции, т.е. амплитудный спектр определяется выражением

.

При , , при , .

Спектр прямоугольного импульса приведен на рис. 7.

Рис. 7. Спектр прямоугольного импульса

Спектр прямоугольного импульса сплошной и простирается от 0 до , имеет тенденцию к затуханию. Однако разумно предположить, что частоты выше некоторых можно не учитывать, т.к. их вес в форме прямоугольного импульса становится малым. В качестве критерия выбора ширины спектра используется энергетический критерий, согласно которому выбирается так, чтобы энергия отсеченной части была пренебрежимо мала по сравнению с энергией внутри интервала . Для нахождения по этому критерию практической ширины спектра используется равенство Парсеваля, связывающее энергию сигнала с энергией спектра

.

Полагая значимую долю энергии равной kE (коэффициент k<1, но достаточно близок к 1) практическая ширина спектра определяется из равенства

,

где w_c - частота среза.

В зависимости от выбранной частоты среза большая или меньшая доля энергии импульса будет сохраняться. На рис. 8 приведен график зависимости сохраняемой энергии импульса от величины .

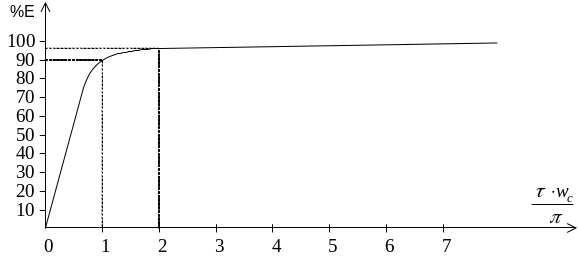
Рис. 8. Зависимость сохраняемой энергии от величины

Для практики передачи сигналов достаточно, чтобы передавалось 96% от максимальной энергии импульса. Поэтому достаточно взять равным 2, т.е.

.

Отсюда линейная частота среза по этому критерию равна

.

Пример. Длительность прямоугольного импульса равна 20 нс. Определить требующуюся полосу пропускания для данного импульса.

По формуле находим .