
- •Теория множеств, действия над множествами. Конечные, счетные и несчетные множества. Счетность множества рациональных чисел q.
- •Понятие поля, упорядоченного поля. Точная верхняя и нижняя грани ограниченного множества. Необходимое и достаточное условие существования точней верхней грани множества. Примеры.
- •Замечание
- •Доказательство
- •Монотонные последовательности, существование предела у ограниченной монотонно последовательности. Неравенство Бернулли, второй замечательный предел.
- •Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
- •Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
- •Непрерывные функции. Непрерывность простейших элементарных функций. Класс элементарных функций, непрерывность его элементов.
- •12) Предел функции в бесконечности и предел функции, равный бесконечности. Предел функции в бесконечности
- •13) Бесконечно малые и бесконечно большие функции, из связь. Свойства бесконечно малых(конечная сумма, произведение б.М. На ограниченную функцию). Сравнение бм и ббфунций.
- •Производная. Геометрический и механический смысл производной
- •16) Производная сложной функции. Примеры. Производная обратной функции. Вывод производной для арксин, арктг.
- •19)Диффернцирование функции одной переменной. Инвариантность первого дифференциала.
- •20) Старшие производные. Формула Лейбница. Примеры.
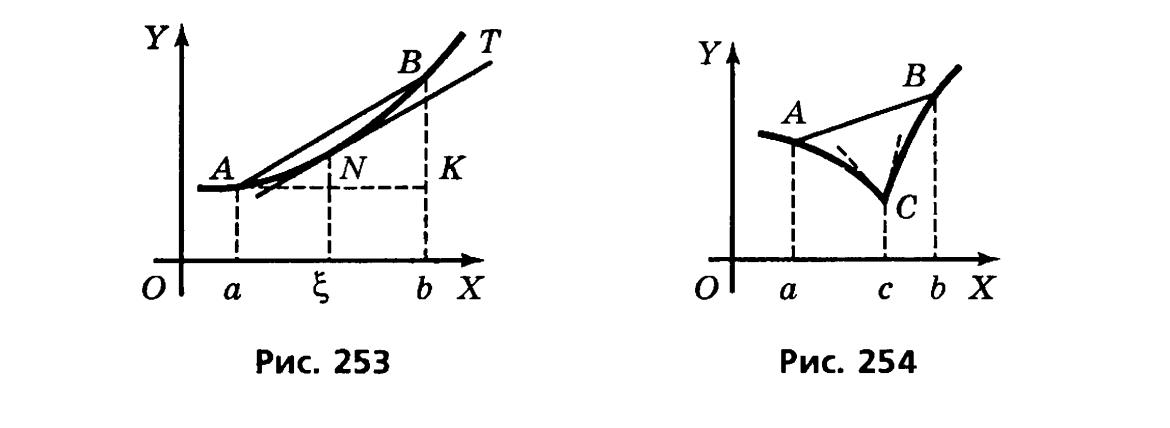
- •21) Свойства функций, дифференцируемых на отрезке. Теорема Ферма. Теорема Ролля и ее геометрический смысл. Теорема Лагранжа и ее геометрический смысл. Теорема Коши.
- •22) Правило Лопиталя. Раскрытие неопределенностей.
- •23) Многочлен Тейлора. Формула Тейлора с остаточным членом в форме Лагранжа, Пеано.
- •24) Разложение основных элментарных функций в ряд Маклорена.
- •25) Локальный Экстремум функции одной переменной, необходимые и достаточные условия.
19)Диффернцирование функции одной переменной. Инвариантность первого дифференциала.

20) Старшие производные. Формула Лейбница. Примеры.
Производная у'=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка.
Если
функция ƒ'(х) дифференцируема, то ее
производная называется производной
второго порядка и обозначается у"
![]()
![]()
Итак, у"=(у')'.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или ƒ'"(х)). Итак, у'"=(y")'


21) Свойства функций, дифференцируемых на отрезке. Теорема Ферма. Теорема Ролля и ее геометрический смысл. Теорема Лагранжа и ее геометрический смысл. Теорема Коши.



22) Правило Лопиталя. Раскрытие неопределенностей.



23) Многочлен Тейлора. Формула Тейлора с остаточным членом в форме Лагранжа, Пеано.

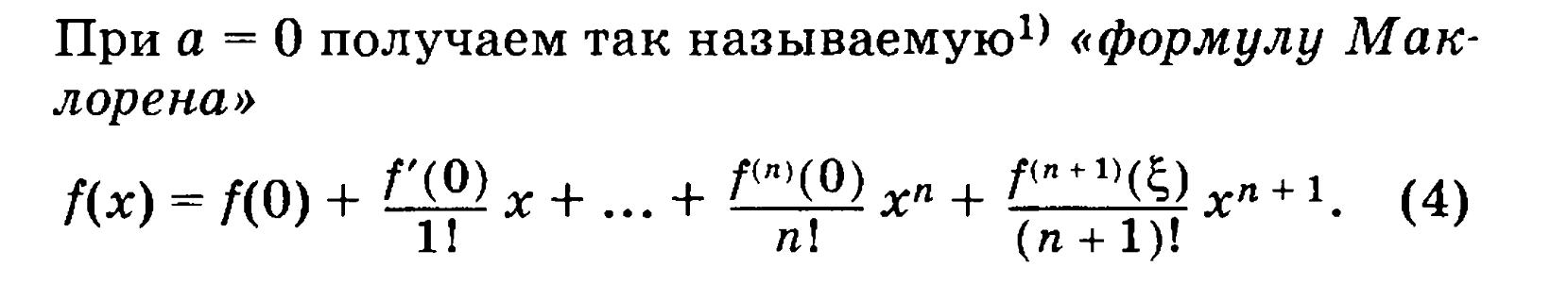
Формула Тейлора с остаточным членом в форме
Лагранжа:
Рассмотрим любую функцию f(x), которая имеетнепрерывные производные всех порядков до (n+1)-го
в некоторой окрестности точки x0. Мы можемформально составить многочленкоторый наз.многочленом Тейлора n-йстепени или n-ммногочленом Тейлора функции f по степеням х–x0.
Многочлен Qn(x) совпадает с функцией f(х) в точке x0но для всех х он не равен f(х) (если f(х) не являетсямногочленом степени n). Кроме того,Q'n(x0)=f'(x0),...,Q(n)n(x0)=f(n)(x0) {2}. Положим f(x)=Qn(x)+rn(x) {3}. Формула {3} носит название формулыТейлора для функции f(x); rn(х) наз. Остаточнымчленом формулы Тейлора, – подробнее, n-мостаточным членом формулы Тейлора функции f пoстепеням х–x0. Функция rn(х) показывает, какуюпогрешность мы допускаем при замене f(x) намногочлен Тейлора {1}.Найдем выражение для rn(х) через производную f(n+1)(х). В силу {2} и {3} rn(x0)=r'n(x0)=...=r(n)n(x0)=0.
Положим (х)=(х–x0)n+1. Ясно, что (x0)=(x0)=...=(n)
(x0)=0. Применяя теорему Коши к функциям rn(х) и
(x), будем иметь
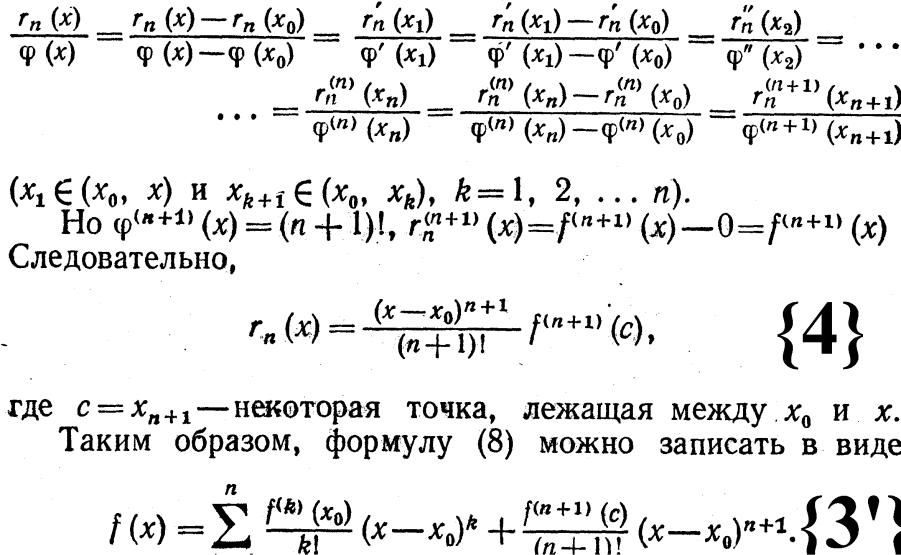
Формула (3') наз. формулой Тейлора с остаточным
членом в форме Лагранжа.
Формула Тейлора с остаточным членом в форме Пеано:
Т![]()
![]() еорема
№1:Если
функция f
имеет в окрестности точки x0непрерывную
производную fn+1(х),
то для любого х из этой окрестности
найдется точка с(х0,х)
такая, что f(x)
можно записать по формуле
еорема
№1:Если
функция f
имеет в окрестности точки x0непрерывную
производную fn+1(х),
то для любого х из этой окрестности
найдется точка с(х0,х)
такая, что f(x)
можно записать по формуле
Здесь с зависит от х и n. Если точка х0=0, то формулу (3') наз. формулой Маклорена. Известны и другие формы остаточного члена формулы Тейлора. Большое значение имеет форма Коши
где (0<<1) зависит от n и х. Уменьшая окрестность точки, получим, что производная f(n+l)(x) есть непрерывная функция от х на замкнутом отрезке [x0–,x0+]. Но тогда она ограничена на этом отрезке:
|![]() f(n+1)(x)|Mn
(x0–xx0+)
{2}.
Здесь Mn–положительное
число, не зависящее от указанных х, но,
вообще говоря, зависящее от n.
Тогда
f(n+1)(x)|Mn
(x0–xx0+)
{2}.
Здесь Mn–положительное
число, не зависящее от указанных х, но,
вообще говоря, зависящее от n.
Тогда
Н![]() еравенство
{3} можно использовать в двух целях: для
того чтобы исследовать поведение rn(х)
при фиксированном n в окрестности
точки и для того, чтобы исследовать
поведение rn(х)
при n.
Из {3}, например, следует, что при
фиксированном n имеет место свойство
rn(x)=o((x–x0)n),
xx0
{4},
показывающее, что если rn(х)
разделить на (х–x0)n,
то полученное частное будет продолжать
стремиться к нулю при xx0.
В силу (13) из (8') следует:
еравенство
{3} можно использовать в двух целях: для
того чтобы исследовать поведение rn(х)
при фиксированном n в окрестности
точки и для того, чтобы исследовать
поведение rn(х)
при n.
Из {3}, например, следует, что при
фиксированном n имеет место свойство
rn(x)=o((x–x0)n),
xx0
{4},
показывающее, что если rn(х)
разделить на (х–x0)n,
то полученное частное будет продолжать
стремиться к нулю при xx0.
В силу (13) из (8') следует:
Эта формула наз. формулой Тейлора с остаточным членом в смысле Пеано. Она приспособлена для изучения функции f в окрестности точки x0.
