Производная. Геометрический и механический смысл производной

 

Производная. Приращение аргумента. Приращение функции.

Дифференцируемая функция. Геометрический смысл производной.

Угловой коэффициент касательной. Уравнение касательной.

Механический смысл производной. Средняя и мгновенная скорость.

Ускорение.

 

 

Производная. Рассмотрим некоторую функцию  y = f ( x ) в двух точках  x₀  и  x₀ +  :  f ( x₀ ) и  f ( x₀ +   ). Здесь через   обозначено некотороемалое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции:  f ( x₀ +   )  f ( x₀ )называется приращением функции. Производной функции  y = f ( x ) в точке  x₀  называется предел:

Если этот предел существует, то функция   f ( x )  называется дифференцируемой в точке  x₀ . Производная функции   f ( x ) обозначается так:

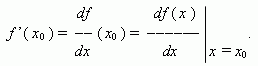
Геометрический смысл производной.  Рассмотрим график функции  y = f ( x ): 

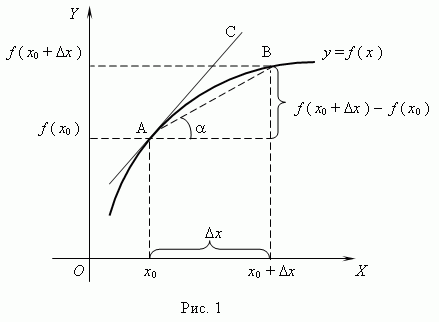
Из рис.1  видно, что для любых двух точек A и B графика функции:  

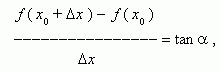
где    - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точкуB, то    неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x₀ ,  f ( x₀  ) ). В общем случае уравнение прямой с угловым коэффициентом  f ’( x₀ )  имеет вид: 

y = f ’( x₀ ) · x + b .

Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:

f ( x₀ ) = f ’( x₀ ) · x₀ + b ,

отсюда,  b =  f ( x₀ ) – f ’( x₀ ) · x₀ , и подставляя это выражение вместо  b, мы получим  уравнение касательной:

y =  f ( x₀ ) +  f ’( x₀ ) · ( x – x₀  ) .

Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки – известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до  t₀ +    точка перемещается на расстояние:  x ( t₀ +   )  x ( t₀ ) =  , а её средняя скорость равна:  v_a =    . При      0  значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:

отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смысл производной.Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).

Если функция f (x) имет производную в точке x₀, то она непрерывна в этой точке.

Из непрерывности самой функции в точке x₀ не следует существование производной её в этой точке.

Правой (левой) производной называется правый (левый) предел

lim_{ x 0 + 0} y/ x

lim_{ x 0 - 0} y/ x ,

если эти пределы существуют.

Для обозначения правой (левой) производной используют символ: f'(x+0) f'(x-0). Необходимым и достаточным условием существования производной является равенство f'(x+0) = f'(x-0).

Пример 2. Доказать, что f(x) = 3|x|+1 не имеет производной в точке x = 0. Составим  y = 3(0+ x)+1-1=3 x при  x>0. При  x<0  y = -3(0+ x)+1-1=-3 x, значит,

lim_{ x 0-0} y/ x =-3, lim_{ x 0+0} y/ x = 3.

Поэтому данная функция не имеет производной в точке x = 0.

Теорема Если функции u=u(x) и v=v(x) имеют в точке x производные, то сумма (разность), произведение и частное этих функций также имеют производные в этой точке, и справедливы следующие формулы: 1) (u±v)/=u/±v/, 2) (u·v)/=u/v+v/u, 3) (vu)=v2u/v−v/u .

Доказательство Из определения производной:

(u±v)/=limΔx→0Δx[u(x+Δx)±v(x+Δx)]−[u(x)±v(x)]= =limΔx→0Δx[u(x+Δx)−u(x)]±[v(x+Δx)−v(x)]=  .    

=limΔx→0Δxu(x+Δx)−u(x)±limΔx→0Δxv(x+Δx)−v(x)=u/±v/

(u·v)/=limΔx→0Δxu(x+Δx)·v(x+Δx)−u(x)·v(x)±v(x+Δx)·v(x)= limΔx→0Δxu(x+Δx)[v(x+Δx)−v(x)]+      

+limΔx→0Δxv(x)[u(x+Δx)−u(x)]=uv/+vu/.

(vu)/=limΔx→0Δxv(x+Δx)u(x+Δx)−v(x)u(x)=limΔx→0Δx·v(x+Δx)·v(x)u(x+Δx)·v(x)−u(x)·v(x+Δx)±u(x)·v(x)=v2u/v−v/u.

Теорема доказана.

Производная степенной функции.

y=xμ,μ∈R.

 y/=limΔx→0ΔxΔy=limΔx→0Δx(x+Δx)μ−xμ=limΔx→0Δxxμ[(xx+Δx)−1]=limΔx→0xΔx·xxμ[(1+xΔx)−1]=  =limΔx→0xΔxxμ−1[(1+xΔx)−1]=[xΔx=t,Δx→0,t→0]=limt→0xμt(1+t)μ−1=xμ·μ,    

[xμ]/=μ·xμ−1.

 

Производная логарифмической функции.

y=logax,

 y/=limΔx→0ΔxΔy=limΔx→0Δxloga(x+Δx)−logax=limΔx→0Δxloga(xx+Δx)=limΔx→0xxΔxloga(1+xΔx)=  =limΔx→0x1·loga(1+xΔx)·1xΔx=[t=xΔx,Δx→0,t→0]=limt→0x1·t1·loga(1+t)=x1limt→0loga(1+t)t1=  =x1loga[limt→0(1+t)t1]=x1logae=1xlna,    

[logax]/=1xlna.

 

Производная показательной функции.

y=ax,

y/=limΔx→0ΔyΔx=limΔx→0Δxax+Δx−ax=limΔx→0Δxax(aΔx−1)=axlna,

[ax]/=axlna.

 

Производные тригонометрических функций.

y=sinx,

y/=limΔx→0Δxsin(x+Δx)−sinx=limΔx→0Δx2sin2Δxcos22x+Δx=limΔx→0Δx22Δxcos(x+2Δx)=cosx,(sinx)/=cosx.

(cosx)/=−sinx.

y=tgx,

y/=cos2x(sinx)/cosx−(cosx)/sinx=cos2xcos2x+sin2x=1cos2x,

(tgx)/=1cos2x.

(ctgx)/=−1sin2x.