
- •Теория множеств, действия над множествами. Конечные, счетные и несчетные множества. Счетность множества рациональных чисел q.
- •Понятие поля, упорядоченного поля. Точная верхняя и нижняя грани ограниченного множества. Необходимое и достаточное условие существования точней верхней грани множества. Примеры.
- •Замечание
- •Доказательство
- •Монотонные последовательности, существование предела у ограниченной монотонно последовательности. Неравенство Бернулли, второй замечательный предел.
- •Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
- •Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
- •Непрерывные функции. Непрерывность простейших элементарных функций. Класс элементарных функций, непрерывность его элементов.
- •12) Предел функции в бесконечности и предел функции, равный бесконечности. Предел функции в бесконечности
- •13) Бесконечно малые и бесконечно большие функции, из связь. Свойства бесконечно малых(конечная сумма, произведение б.М. На ограниченную функцию). Сравнение бм и ббфунций.
- •Производная. Геометрический и механический смысл производной
- •16) Производная сложной функции. Примеры. Производная обратной функции. Вывод производной для арксин, арктг.
- •19)Диффернцирование функции одной переменной. Инвариантность первого дифференциала.
- •20) Старшие производные. Формула Лейбница. Примеры.
- •21) Свойства функций, дифференцируемых на отрезке. Теорема Ферма. Теорема Ролля и ее геометрический смысл. Теорема Лагранжа и ее геометрический смысл. Теорема Коши.
- •22) Правило Лопиталя. Раскрытие неопределенностей.
- •23) Многочлен Тейлора. Формула Тейлора с остаточным членом в форме Лагранжа, Пеано.
- •24) Разложение основных элментарных функций в ряд Маклорена.
- •25) Локальный Экстремум функции одной переменной, необходимые и достаточные условия.
12) Предел функции в бесконечности и предел функции, равный бесконечности. Предел функции в бесконечности
Пусть функция f(x) определена на (a, + ∞).
Число A называется пределом функции f(x) при x → + ∞ (обозначается A =
lim |
x → + ∞ |
f(x) ), если
|
ε > 0 N: x > N |f(x) − a| < ε. |
|
Пусть функция f(x) определена на ( − ∞,a).
Число A называется пределом функции f(x) при x → − ∞ (обозначается A =
lim |
x → − ∞ |
f(x) }, если
|
ε > 0 N: x < − N |f(x) − a| < ε. |
|
Если существуют пределы функции f(x) при x → + ∞ и при x → − ∞ и они равны одному и тому же числу A, то это число A называется пределом функции f(x) при x → ∞ {обозначается A =
lim |
x → ∞ |
f(x) .
Теоремы о пределах последовательностей и правила их вычисления распространяются и на пределы функций в бесконечности.
Наклонные асимптоты графика функции
Пусть функция f(x) определена на (a, + ∞). Обозначим символом α разность ординат точек графика функции f(x ) и прямой y = kx + b при одном и том же значении x (рис. 1), т.е. α(x) = f(x) − (kx + b).
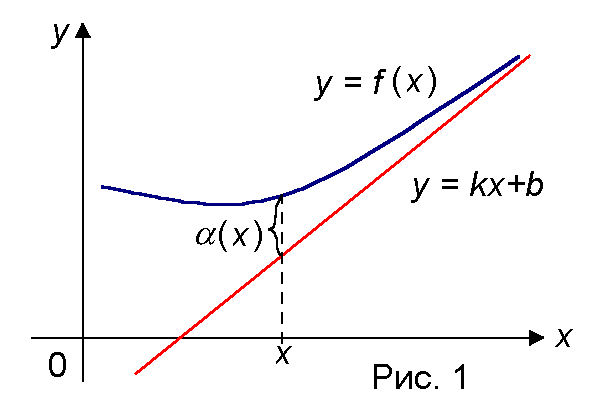
Если
lim |
x → + ∞ |
α(x) = 0, то прямая y = kx + b называется (правой) асимптотой графика функции y = f(x) при x → + ∞ .
Теорема 1. Прямая y = kx + b является (правой) асимптотой графика y = f(x) при x → + ∞ тогда и только тогда, когда существуют конечные пределы, определяющие параметры асимптоты:
|
k =
, b =
[f(x) − kx]. |
(1) |
Если хотя бы один из этих пределов не существует или бесконечен, то график y = f(x) не имеет правой асимптоты.
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 36.
Если
lim |
x → − ∞ |
α(x) = 0, то прямая y = kx + b называется (левой) асимптотой графика функции y = f(x) при x → − ∞.
Если
lim |
x → ∞ |
α(x) = 0, то прямая y = kx + b называется (двусторонней) асимптотой графика функции y = f(x) при x → ∞.
Существование левой и двусторонней асимптот графика функции y = f(x) определяется аналогично теореме 1, т.е. существованием пределов типа (1) при x → − ∞ и x → ∞ соответственно.
При k ≠ 0 асимптоты называются наклонными, при k = 0 — горизонтальными.
Предел функции, равный бесконечности - ???
13) Бесконечно малые и бесконечно большие функции, из связь. Свойства бесконечно малых(конечная сумма, произведение б.М. На ограниченную функцию). Сравнение бм и ббфунций.
СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ
И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ
Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.
Доказательство. Возьмем
произвольное число ε>0 и
покажем, что при некотором δ>0 (зависящим
от ε) при всех x,
для которых |x
– a|<δ,
выполняется неравенство ![]() ,
а это и будет означать, что 1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) –
бесконечно большая функция при x→a,
то найдется δ>0 такое,
что как только |x
– a|<δ,
так |f(x)|>1/ ε.
Но тогда для тех же x
.
,
а это и будет означать, что 1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) –
бесконечно большая функция при x→a,
то найдется δ>0 такое,
что как только |x
– a|<δ,
так |f(x)|>1/ ε.
Но тогда для тех же x
.
Примеры.
Ясно, что при x→+∞ функция y=x2+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция
 –
бесконечно малая при x→+∞,
т.е.
–
бесконечно малая при x→+∞,
т.е. 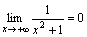 .
.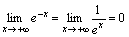 .
.
Можно доказать и обратную теорему.
Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.
Доказательство теоремы проведите самостоятельно.
Примеры.
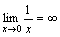 .
.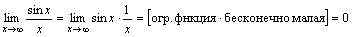 .
.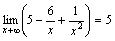 ,
так как функции
,
так как функции 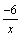 и
и  -
бесконечно малые при x→+∞,
то
-
бесконечно малые при x→+∞,
то 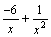 ,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же  является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0
![]() .
.
Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.
Доказательство.
Приведем доказательство для двух
слагаемых. Пусть f(x)=α(x)+β(x),
где ![]() и
и ![]() .
Нам нужно доказать, что при произвольном
как угодно малом ε>0
найдетсяδ>0,
такое, что для x,
удовлетворяющих неравенству |x
– a|<δ,
выполняется |f(x)|< ε.
.
Нам нужно доказать, что при произвольном
как угодно малом ε>0
найдетсяδ>0,
такое, что для x,
удовлетворяющих неравенству |x
– a|<δ,
выполняется |f(x)|< ε.
Итак, зафиксируем произвольное число ε>0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ1>0, что при |x – a|<δ1 имеем |α(x)|< ε/2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ2>0, что при |x – a|<δ2 имеем | β(x)|< ε/2.
Возьмем δ=min{ δ1, δ2}.Тогда в окрестности точки a радиуса δбудет выполняться каждое из неравенств |α(x)|< ε/2 и | β(x)|< ε/2. Следовательно, в этой окрестности будет
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,
т.е. |f(x)|<ε, что и требовалось доказать.
Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.
Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.
Из доказанной теоремы вытекают:
Следствие
1. Если
и
,
то ![]() .
.
Следствие
2. Если
и c=const,
то ![]() .
.
14) Эквивалентность б.м.. Основные эквивалентности, связанные с первым и вторым замечательными пределами. Теорема о замене на эквивалентные функции в пределе отношения двух б.м.\б.б. функций.
Эквивалентные бесконечно малые и основные теоремы о них
Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые.
Если ![]() то
α и ß называются эквивалентными
бесконечно малыми (при
х→x0);
это обозначается так: α~ß.
то
α и ß называются эквивалентными
бесконечно малыми (при
х→x0);
это обозначается так: α~ß.
Например,
sinx~х при х→0, т.к ![]() при
x→0, т. к.
при
x→0, т. к. ![]()
Теорема 18.1 . Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.
Теорема 18.2 . Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.

Справедливо и обратное утверждение: если разность б.м.ф. α и ß есть бесконечно малая высшего порядка, чем α или ß, то α и ß — эквивалентные бесконечно малые.
Действительно, так как
![]() т.
е.
т.
е. ![]() Отсюда
Отсюда ![]() т. е. α~ß. Аналогично, если
т. е. α~ß. Аналогично, если![]() то
α~ß.
то
α~ß.
Теорема 18.3 . Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.
Докажем
теорему для двух функций. Пусть α→0, ß→0
при х→хо,
причем α — б.м.ф. высшего порядка, чем
ß, т. е. ![]() .
Тогда
.
Тогда
![]()
Следовательно, α+ß~ß при х→х0.
Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой суммы.
Замена суммы б.м.ф. ее главной частью называется отбрасыванием бесконечно малых высшего порядка.
<< Пример 18.5
α(x)→0
1 |
sinα(x)~α(x) |
2 |
arcsinα(x)~α(x) |
3 |
tgα(x)~α(x) |
4 |
arctgα(x)~α(x) |
5 |
loga(1+α(x))~(logae)α(x) |
6 |
ln(1+α(x))~α(x) |
7 |
aα(x)-1~α(x)lna,a>0,a≠1 |
8 |
eα(x)-1~α(x) |
9 |
(1+α(x))μ-1~μα(x) |
10 |
1+α(x)n-1~α(x)n |
11 |
1+α(x)-1~α(x)2 |
12 |
1-cosα(x)~12α2(x) |
15) Дифференцируемые функции. Производная, дифференциал, их геометроический и механический смысл. Необходимое и достаточное условие существования производной для функции одной переменной. Нахождение производной суммы, произведения и частного двух функций. Вывод формул производной для основных элементарных функций.
Согласно общему определению функция
![]()
одной переменной является дифференцируемой в точке x0 своей области определения M, если существуют такие константы a и b, что для любой точки x области M верно
f(x) = a + b(x − x0) + o(x − x0);
при этом число a неизбежно равно значению функции в точке x0, а число b -- пределу
![]() ,
,
который, следовательно, существует и его, как известно, называют производной функции в точке x0, то есть
f(x) = f(x0) + f'(x0)(x − x0) + o(x − x0).
Более того, функция одной переменной является дифференцируемой в точке x0 тогда и только тогда, она имеет производную в этой точке.
График функции y = f(x) представляет собой кривую на плоскости Oxy, а график линейной функции
y = f(x0) + f'(x0)(x − x0)
доставляет касательную прямую к этой кривой, проведённую в точке x0.
Напр., функция f(x) = x2 определена и дифференцируема в любой вещественной точке, поскольку её можно представить в виде
f(x) = f(x0) + 2x0(x − x0) + (x − x0)2.
При
этом её производная есть f'(x0)
= 2x0,
а уравнение касательной прямой,
проведённой в точке x0,
имеет вид: ![]() .
.
Элементарные
функции могут быть непрерывны в некоторой
точке, но не быть в ней дифференцируемы.
Напр., функция f(x)
= | x | является
непрерывной на всей вещественной оси,
но её производная испытывает скачок
при переходе через точку x =
0,
в котором эта функция не является
дифференцируемой. В этой точке нельзя
провести и касательную к графику функции.
Функция ![]() тоже
непрерывна на всей вещественной оси и
её график имеет касательные во всех
точках, однако касательная, проведённая
в точке x =
0,
является вертикальной прямой и поэтому
производная функции
бесконечно
велика в точке x =
0,
а сама функция не дифференцируема в
этой точке.
тоже
непрерывна на всей вещественной оси и
её график имеет касательные во всех
точках, однако касательная, проведённая
в точке x =
0,
является вертикальной прямой и поэтому
производная функции
бесконечно
велика в точке x =
0,
а сама функция не дифференцируема в
этой точке.
Графики элементарных функций учат, что произвольная функция дифференцируема всюду, за исключением исключительных и изолированных значений аргумента. Первая попытка аналитического доказательства этого утверждения принадлежит Амперу[1], и поэтому оно носит название гипотезы Ампера. Это утверждение, однако, не верно в классе аналитически представимых функций, напр., функция Дирихле не является даже непрерывной ни в одной точке[2]. Нельзя также считать и произвольную непрерывную функцию дифференцируемой, напр., функция Вейерштрассаопределена и непрерывная на всей вещественной оси, но не является дифференцируемой ни в одной её точке[3]. Это в частности означает, что к её графику ни в одной точке нельзя провести касательную прямую. Тем не менее, гипотезу Ампера можно рассматривать как нестрогую формулировку следующей теоремы Лебега: любая монотонная функция f(x) имеет определённую конечную производную всюду, кроме, быть может, некоторого множества значений x меры нуль.[4]
