
- •Теория множеств, действия над множествами. Конечные, счетные и несчетные множества. Счетность множества рациональных чисел q.
- •Понятие поля, упорядоченного поля. Точная верхняя и нижняя грани ограниченного множества. Необходимое и достаточное условие существования точней верхней грани множества. Примеры.
- •Замечание
- •Доказательство
- •Монотонные последовательности, существование предела у ограниченной монотонно последовательности. Неравенство Бернулли, второй замечательный предел.
- •Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
- •Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
- •Непрерывные функции. Непрерывность простейших элементарных функций. Класс элементарных функций, непрерывность его элементов.
- •12) Предел функции в бесконечности и предел функции, равный бесконечности. Предел функции в бесконечности
- •13) Бесконечно малые и бесконечно большие функции, из связь. Свойства бесконечно малых(конечная сумма, произведение б.М. На ограниченную функцию). Сравнение бм и ббфунций.
- •Производная. Геометрический и механический смысл производной
- •16) Производная сложной функции. Примеры. Производная обратной функции. Вывод производной для арксин, арктг.
- •19)Диффернцирование функции одной переменной. Инвариантность первого дифференциала.
- •20) Старшие производные. Формула Лейбница. Примеры.
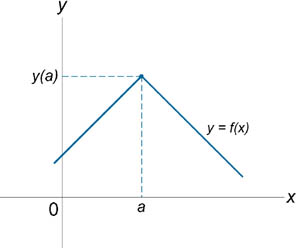
- •21) Свойства функций, дифференцируемых на отрезке. Теорема Ферма. Теорема Ролля и ее геометрический смысл. Теорема Лагранжа и ее геометрический смысл. Теорема Коши.
- •22) Правило Лопиталя. Раскрытие неопределенностей.
- •23) Многочлен Тейлора. Формула Тейлора с остаточным членом в форме Лагранжа, Пеано.
- •24) Разложение основных элментарных функций в ряд Маклорена.
- •25) Локальный Экстремум функции одной переменной, необходимые и достаточные условия.
Непрерывные функции. Непрерывность простейших элементарных функций. Класс элементарных функций, непрерывность его элементов.
Непрерывность элементарных функций.
1)Непрерывность функции ax, a>0.
Справедливо
равенство  .
.
a)
Если a>1, обозначим 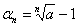 ,
a=(n+1)n
>nn, n<a/n
, следовательно n
– б.м..
,
a=(n+1)n
>nn, n<a/n
, следовательно n
– б.м..
Замечание.
Отметим, что точно также можно доказать
равенство  .
Именно,
.
Именно, ![]() ,
n=(n+1)n
>
,
n=(n+1)n
> 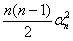 , n<
, n<![]() ,
следовательно n
– б.м..
,
следовательно n
– б.м..
b) Если a <1,
 то
то  ,
b > 1.
,
b > 1.
Докажем,
что ![]() (непрерывность
в 0 функции ax ).
(непрерывность
в 0 функции ax ).
1 a> 1
Пусть
{xk} последовательность типа Гейне для
0+0, то есть xk0,
xk>0. Можно считать, что xk< 1. Для
последовательности целых частей
дроби ![]() будут
выполнены неравенства
будут
выполнены неравенства 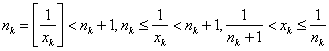 .
Откуда, в частности, следует, что
nk+ и
.
Откуда, в частности, следует, что
nk+ и ![]() далее,
переходя к пределу при k ,
получим требуемое равенство.
далее,
переходя к пределу при k ,
получим требуемое равенство.
Аналогично рассматривается случай x 0 - 0. Из существования и равенства односторонних пределов следует доказываемое утверждение .
2 Если a<1, тоbx=1/ax, b=1/a > 1.
2)
Функция ax непрерывна в точке x0 . Это
следует из равенства ![]() .
.
3). Функция y=logax непрерывна, как обратная к непрерывной строго монотонной функции x=a y .
4). Степенная функция y=x. Докажем непрерывность при x>0. Имеем x=e ln x, далее теорема о непрерывности суперпозиции.
Класс элементарных функций
Простейшими элементарными функциями обычно называют линейную (y=kx+b), квадратичную (y=ax2+bx+c), степенную (y=xn, где n целое число, не равно 1), показательную (y=ax,где a больше 0 и не равно 1), логарифмическую (y=loga x, где a больше 0 и не равно 1), тригонометрические (y=sin x, y=cos x, y=tg x, y=ctg x), обратные тригонометрические (y=arcsin x, y=arccos x, y=arctg x, y=arcctg x).
К элементарным функциям относятся основные элементарные функции и те, которые можно образовать из них с помощью конечного числа операций (сложения, вычитания, умножения и деления) и суперпозиций.
Выделим классы функций, которые получены из элементарных:
Целая рациональная функция (или многочлен): y=a0xn+a1xn-1+...+an, где n - целое неотрицательное число (степень многочлена), a0, a1, ..., an - постоянные числа (коэффициенты).
Дробно-рациональная функция, которая является отношением двух целых рациональных функций.
Целые рациональные и дробно-рациональные образуют класс рациональных функций.
Иррациональная функция - это та, которая строится с помощью суперпозиции рациональной функции и степенных функций с рациональными показателями.
11) Точки разрыва функций и их классификация.
|
||||||||||||||||||||||||




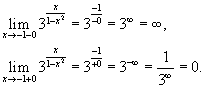
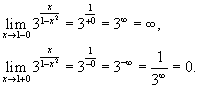
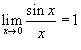 ,
то в данной точке существует
устранимый разрыв. Мы можем
сконструировать новую функцию
,
то в данной точке существует
устранимый разрыв. Мы можем
сконструировать новую функцию