
- •Теория множеств, действия над множествами. Конечные, счетные и несчетные множества. Счетность множества рациональных чисел q.
- •Понятие поля, упорядоченного поля. Точная верхняя и нижняя грани ограниченного множества. Необходимое и достаточное условие существования точней верхней грани множества. Примеры.
- •Замечание
- •Доказательство
- •Монотонные последовательности, существование предела у ограниченной монотонно последовательности. Неравенство Бернулли, второй замечательный предел.
- •Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
- •Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
- •Непрерывные функции. Непрерывность простейших элементарных функций. Класс элементарных функций, непрерывность его элементов.
- •12) Предел функции в бесконечности и предел функции, равный бесконечности. Предел функции в бесконечности
- •13) Бесконечно малые и бесконечно большие функции, из связь. Свойства бесконечно малых(конечная сумма, произведение б.М. На ограниченную функцию). Сравнение бм и ббфунций.
- •Производная. Геометрический и механический смысл производной
- •16) Производная сложной функции. Примеры. Производная обратной функции. Вывод производной для арксин, арктг.
- •19)Диффернцирование функции одной переменной. Инвариантность первого дифференциала.
- •20) Старшие производные. Формула Лейбница. Примеры.
- •21) Свойства функций, дифференцируемых на отрезке. Теорема Ферма. Теорема Ролля и ее геометрический смысл. Теорема Лагранжа и ее геометрический смысл. Теорема Коши.
- •22) Правило Лопиталя. Раскрытие неопределенностей.
- •23) Многочлен Тейлора. Формула Тейлора с остаточным членом в форме Лагранжа, Пеано.
- •24) Разложение основных элментарных функций в ряд Маклорена.
- •25) Локальный Экстремум функции одной переменной, необходимые и достаточные условия.
Монотонные последовательности, существование предела у ограниченной монотонно последовательности. Неравенство Бернулли, второй замечательный предел.
Последовательность элементов множества называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.
—
неубывающая ![]()
Последовательность элементов множества называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.
—
невозрастающая ![]()
Последовательность элементов множества называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий.
—
возрастающая ![]()
Последовательность элементов множества называется убывающей, если каждый элемент этой последовательности превышает следующий за ним.
—
убывающая ![]()
Последовательность называется монотонной, если она является неубывающей, либо невозрастающей.[1]
Последовательность называется строго монотонной, если она является возрастающей, либо убывающей.
Свойства
Ограниченность.
Всякая неубывающая последовательность ограничена снизу.
Всякая невозрастающая последовательность ограничена сверху.
Всякая монотонная последовательность ограничена по крайней мере с одной стороны.
Монотонная последовательность сходится тогда и только тогда, когда она ограничена с обеих сторон.(Теорема Вейерштрасса об ограниченных монотонных последовательностях)
Сходящаяся неубывающая последовательность ограничена сверху своим пределом.
Сходящаяся невозрастающая последовательность ограничена снизу своим пределом.
Теорема:
1.
Если последовательность ![]() монотонно
возрастает и ограниченна сверху, то она
сходится к конечному пределу;
монотонно
возрастает и ограниченна сверху, то она
сходится к конечному пределу;
2.
Если последовательность
монотонно
возрастает, но неограниченна сверху,
то ![]() .
.
Доказательство.
Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
Вспомним
свойства ![]() .
Их было два
.
Их было два
Но
учтем теперь что ![]() .
Это значит, что
.
Это значит, что ![]()
![]() .
Тогда имеем следующую цепочку неравенств
.
Тогда имеем следующую цепочку неравенств
![]()
Выбрасывая
лишнее получим, что
![]() или
или ![]() ,
что и говорит о том, что
,
что и говорит о том, что ![]() .
.
Заметьте, что предел равен как раз супремуму множества .
Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
Но
.
Значит,
и
поэтому можно записать
![]() .
Выбрасывая в этом неравенстве
.
Выбрасывая в этом неравенстве ![]() ,
получим окончательно
,
получим окончательно
![]()
что и говорит о том, что .
Неравенство Бернулли
Нера́венство Берну́лли утверждает:
если ![]() ,
то
,
то
![]() для
всех
для
всех ![]()
[править]Доказательство
Доказательство
неравенства ![]() проводится
методом математической
индукции по n.
При n =
0 неравенство, очевидно, верно. Допустим,
что оно верно для n,
докажем его верность для n+1:
проводится
методом математической
индукции по n.
При n =
0 неравенство, очевидно, верно. Допустим,
что оно верно для n,
докажем его верность для n+1:
![]() ,
,
ч.т.д.
Второй зам. Предел
Второй замечательный предел
![]() или
или ![]()
Доказательство второго замечательного предела:
Доказательство для натуральных значений x [показать]
![]() Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел длявещественных
x, то есть докажем, что
Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел длявещественных
x, то есть докажем, что ![]() .
Рассмотрим два случая:
.
Рассмотрим два случая:
1.
Пусть ![]() .
Каждое значение x заключено между двумя
положительными целыми числами:
.
Каждое значение x заключено между двумя
положительными целыми числами: ![]() ,
где
,
где ![]() —
это целая часть x.
—
это целая часть x.
Отсюда
следует: ![]() ,
поэтому
,
поэтому
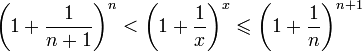 .
.
Если
,
то ![]() .
Поэтому, согласно пределу
.
Поэтому, согласно пределу ![]() ,
имеем:
,
имеем:
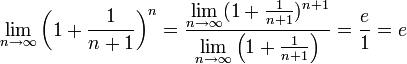
![]() .
.
По
признаку (о пределе промежуточной
функции) существования пределов ![]() .
.
2.
Пусть ![]() .
Сделаем подстановку − x = t,
тогда
.
Сделаем подстановку − x = t,
тогда
![]()
![]() .
.
Из
двух этих случаев вытекает, что
для
вещественного x. ![]()
Следствия
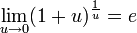
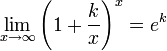


 для
для  ,
, 

Определение предела функции в точке по Коши и по Гейне. Равносильность этих определений. Критерий Коши существования конечного предела функции. Односторонние пределы.
Предел функции по Гейне
Значение ![]() называется пределом (предельным
значением)
функции
называется пределом (предельным
значением)
функции ![]() в
точке
в
точке ![]() ,
если для любой последовательности точек
,
если для любой последовательности точек ![]() ,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции
,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции ![]() сходится
к
.[1]
сходится
к
.[1]
![]()
Предел функции по Коши
Значение
называется пределом (предельным
значением)
функции
в
точке
,
если для любого наперёд взятого
положительного числа ε найдётся
отвечающее ему положительное число ![]() такое,
что для всех аргументов
,
удовлетворяющих условию
такое,
что для всех аргументов
,
удовлетворяющих условию ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() .[1]
.[1]
![]()
Теорема 8.3 (Критерий Коши для функции)
Если
для любого ![]() существует
такое
существует
такое ![]() ,
что для любых
,
что для любых ![]() из
проколотой окрестности точки a разность
значений функции в этих точках меньше
из
проколотой окрестности точки a разность
значений функции в этих точках меньше![]() ,
то существует предел функции при
,
то существует предел функции при ![]() ,
т.е.
,
т.е. ![]() .
.
Доказательство
Необходимость ![]() .
Пусть существует предел
.
Пусть существует предел ![]() .
Тогда
.
Тогда ![]() .
Так как
.
Так как ![]() ,
то
,
то 
 .
.
Достаточность ![]() .
.
Теорема об эквивалентности двух определений предела:
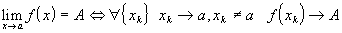 (Определение
предела по Гейне-Борелю).
(Определение
предела по Гейне-Борелю).Применяем критерий Коши для последовательности.
Докажем, что этот предел не зависит от выбора последовательности
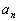 .
Для этого рассмотрим другую извлеченную
последовательность
.
Для этого рассмотрим другую извлеченную
последовательность 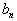 ,
тоже сходящуюся к a.
Соответствующая ей последовательность
,
тоже сходящуюся к a.
Соответствующая ей последовательность 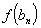 сходится
к пределу B.
Для доказательства, что A=B,
допустим противное. Рассмотрим
последовательность:
сходится
к пределу B.
Для доказательства, что A=B,
допустим противное. Рассмотрим
последовательность: 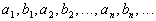 ,
сходящуюся к a.
Последовательность значений функции
,
сходящуюся к a.
Последовательность значений функции 
не имеет предела, т.к. ее четные и нечетные члены сходятся к разным пределам A и B соответственно. Таким образом, получилось противоречие.
Односторонний предел по Гейне
Число
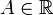 называется правосторонним
пределом (правым
пределом, пределом
справа)
функции
в
точке
,
если для всякой последовательности
,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции
сходится
к числу
.
называется правосторонним
пределом (правым
пределом, пределом
справа)
функции
в
точке
,
если для всякой последовательности
,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции
сходится
к числу
.
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякой последовательности , состоящей из точек, меньших числа , которая сама сходится к числу , соответствующая последовательность значений функции сходится к числу .[1]
![]()
[править]Односторонний предел по Коши
Число называется правосторонним пределом (правым пределом, пределом справа) функции в точке , если для всякого положительного числа
 отыщется
отвечающее ему положительное
число
отыщется
отвечающее ему положительное
число 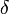 такое,
что для всех
точек
из интервала
такое,
что для всех
точек
из интервала 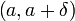 справедливо неравенство
.
справедливо неравенство
.
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякого положительного числа отыщется отвечающее ему положительное число такое, что для всех точек из интервала
 справедливо
неравенство
.[1]
справедливо
неравенство
.[1]
![]()
Локальные свойства функций, имеющих конечный предел в точке : единственность предела, локальная ограниченность функции, сохранение знака функции в окрестности точки х0 (если предел функции не равен нулю). Теоремы о пределе суммы, разности, частного.
Алгебраические свойства функций, имеющих конечный предел в точке а.
Пусть
 ,
тогда:
,
тогда:
Существует предел алгебраической суммы этих ф-ий,равный алгебраической сумме этих пределов.
![]()
Существует предел произведения ф-ий произведение пределов
![]()
Если предел знаменателя неравен 0 и Bнеравно 0 то
![]()

Следствие.
Из 1 и 2 следует, что константы можно выносить за знак предела
![]()
Единственность предела
Если функция или последовательность имеет предел, то он единственнен. Доказывается так. Возьмем два числа А1 и А2 и пусть они оба пределы последовательности x(n). Тогда для всех n начиная с некоторого N для произвольно взятого числа эпсилон выполняются неравенства модуль(x(n) - A1) <= эпсилон и модуль(x(n) - A2) <= эпсилон. Раскрывая эти неравенства, получаем A1 - эпсилон <= x(n) <= А1+ эпсилон и A2 - эпсилон <= x(n) <= А2+ эпсилон. Если А1 и А2 различны, то может быть, например А1 < А2. Тогда можно подобрать такое эпслон, что будет выполняться только одно из неравенств, а другое выполняться не будет. А должны выполняться оба неравенства сразу при любом эпсилон.
Теоремы о пределе суммы, разности, частного
Т.3:
Предел суммы конечного числа функций,
имеющих пределы при х![]() а,
равен сумме их пределов
а,
равен сумме их пределов
Пусть![]() тогда
по теореме 2 име-
тогда
по теореме 2 име-
ем![]() где
где![]() —
б.м. при
—
б.м. при
х![]() а,
следовательно,
а,
следовательно,![]() Используя
лемму 1 о б.м., заключаем, что
Используя
лемму 1 о б.м., заключаем, что![]() —
б.м. при
—
б.м. при
![]() и
по теореме 2 получаем равенство
и
по теореме 2 получаем равенство![]() b1
+ b2
b1
+ b2
Т.4:
Предел произведения конечного числа
функций, имеющих пределы при х![]() а,
равен произведению пределов Методика
доказательства аналогична доказательству
Т.3. Следствие. Постоянный множитель
можно выносить за знак предела.
а,
равен произведению пределов Методика
доказательства аналогична доказательству
Т.3. Следствие. Постоянный множитель
можно выносить за знак предела.
Т.5:
Предел отношения двух функций, имеющих
пределы при х![]() а,
равен отношению их пределов (если предел
знаменателя не нуль), т.е.
а,
равен отношению их пределов (если предел
знаменателя не нуль), т.е.
![]()
Непрерывные функции, их свойства. Непрерывность сложной функции. Глобальные свойства функций, непрерывных на отрезке(прохождение через 0, если f(a) f(b) < 0, теорема о промежуточных значениях, первая и вторая теоремы Вейерштрасса)
Непрерывная функция
Пусть ![]() и
и ![]() .
.
Функция f непрерывна
в точке ![]() ,
если для любого
,
если для любого ![]() существует δ
> 0 такое,
что
существует δ
> 0 такое,
что
![]()
Функция f непрерывна на множестве E, если она непрерывна в каждой точке данного множества.
Локальные свойства
Функция, непрерывная в точке , является ограниченной в некоторой окрестности этой точки.
Если функция
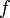 непрерывна
в точке
и
непрерывна
в точке
и  (или
(или 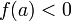 ),
то
),
то 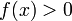 (или
(или  )
для всех
,
достаточно близких к
.
)
для всех
,
достаточно близких к
.Если функции и
 непрерывны
в точке
,
то функции
непрерывны
в точке
,
то функции 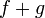 и
и  тоже
непрерывны в точке
.
тоже
непрерывны в точке
.Если функции и непрерывны в точке и при этом
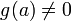 ,
то функция
,
то функция  тоже
непрерывна в точке
.
тоже
непрерывна в точке
.Если функция непрерывна в точке и функция непрерывна в точке
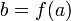 ,
то их композиция
,
то их композиция 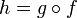 непрерывна
в точке
.
непрерывна
в точке
.еорема о непрерывности сложной функции.
Пусть функция (t) непрерывна в точке t0 и функция f(x) непрерывна в точке х0=(t0). Тогда функция f((t)) непрерывна в точке t0.
Доказательство.
Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем

Выписывая подчеркнутые кванторы, получим, что
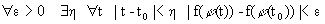 ,
,что и говорит о том, что f((t)) непрерывна в точке t0.
Глобальные свойства функций, непрерывных на отрезке
Если функция у(х) непрерывна на отрезке [a,b] и у(a) =/= у(b), то для любого числа М между у(a) и у(b) найдется внутри (a,b) хотя бы одна точка х0 такая, что у(х0)=М. Доказательство опирается на теорему Коши: Если у(a)*у(b) < 0, то внутри (a,b) найдется хотя бы одна точка х0 такая, что у(х0)=0. Достаточно рассмотреть функцию у(х)-М и сослаться на теорему Коши.
Теорема (первая теорема Вейерштрасса) Если функция непрерывна на сегменте, то она ограничена на нем. Доказательство: методом от противного, воспользуемся свойством замкнутости сегмента [a;b]. Из любой последовательности (xn) этого сегмента можем выделить подпоследовательность xnk, сходящуюся к x0∈[a;b]. Пусть f не ограничена на сегменте [a;b], например, сверху, тогда для всякого натуральногоn∈Nнайдется точка xn∈[a;b], что f(xn)>n. Придавая n значения 1,2,3,{\ldots}, мы получим последовательность (xn) точек сегмента [a;b], для которых выполнено свойствоf(x1)>1,f(x2)>2,f(x3)>3,...,f(xn)>n... Последовательность (xn) ограничена и поэтому из нее по теореме можно выделитьподпоследовательность(xnk), которая сходится к точке x0∈[a;b]: limk→∞xnk=x0 (1) Рассмотрим соответствующую последовательность (f(xnk)). С одной стороны f(xnk)>nk и поэтомуlimk→∞f(xnk)=+∞ (2), С другой стороны, учитывая определение непрерывной функции по Гейне из (1) будем иметьlimk→∞f(xnk)=f(x0) (3) Получаем равенства (2) и (3) противоречат теореме (о единственности предела). Это противоречие и доказывает справедливость теоремы. Аналогично доказывается ограниченность функции снизу. Ч.Т.Д.
Теорема (вторая теорема Вейерштрасса) Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения). Доказательство: Пусть f(x)∈C([a;b]), c=infx∈[a;b]f(x), d=supx∈[a;b]f(x). По первой теореме Вейерштрасса c,d∈R. Докажем, что f достигает на [a;b] своих граней, т.е. найдутся такие точкиx1,x2∈[a;b], чтоf(x1)=c,f(x2)=d. Докажем, например, существование точки x2.
По определению верхней грани имеем (∀x∈[a;b])(f(x)=d). Предположим противное, т.е. точки x2, в которой f(x2)=dна [a;b], тогда на [a;b] выполняется условиеf(x)<d или d−f(x)>0. Далее введем вспомогательную функцию ϕ(x)=1d−f(x) . ϕ(x) на [a;b] положительна и непрерывна (как отношение двух непрерывных на [a;b] функций и d−f(x)/=0) , поэтому по первой Т. Вейерштрасса ϕ(x) на [a;b] ограничена. Это означает, что при некотором М>0 (∀x∈[a;b])(0<1d−f(x)≤M), отсюда имеем f(x)≤d−1M<d. Полученное неравенство противоречит тому, что d является верхней гранью функции f(x) на [a;b], т.е. наименьшим из верхних границ. Полученное противоречие и означает существование точки x2 такой, чтоf(x2)=d.
Аналогично доказывается существование точки x1∈[a;b], такой что f(x1)=c.
Следствие Если f непрерывна и непостоянна на [a;b], то образ этого отрезка [a;b] при отображении f будет так же отрезок, т.е. непрерывный непостоянный образ отрезка есть отрезок. Доказательство: В самом деле образом отрезка [a;b] при отображении f будет отрезок [с;d], где c=inf[a;b]f(x)=min[a;b]f(x), а d=sup[a;b]f(x)=max[a;b]f(x), что следует из второй теоремы Больцано-Коши и второй теоремы Вейерштрасса Ч.Т.Д.
