14. Критерий Коши сходимости последовательностей (без доказательства).

Критерий Коши.

Последовательность {Xn} называется удовлетворяющей условия Коши(или фундаментальной), если каково бы ни было число ε>0, найдется номер N такой, что, начиная с этого номера, все элементы , следующие за Xn ,

отличаются от Xn меньше чем ε.

На языке символов Коши записывается так:

ε >0 ε

15. Последовательности. Теорема Больцано- Вейерштрасса (без доказательства).

Теорема Больца́но — Вейерштрасса гласит, что

1. Из любой ограниченной последовательности вещественных чисел можно выделить сходящуюся подпоследовательность.

2. Из любой неограниченной последовательности можно выделить бесконечно большую последовательность, то есть последовательность, имеющую своим пределом бесконечность определённого знака.

Иначе говоря, замкнутое множество числовой прямой компактно тогда и только тогда, когда оно ограничено.

Из этой теоремы следуют аналогичные утверждения для комплексных чисел и для последовательностей точек n-мерного евклидова пространства.

16. Функция. Предел функции – определение по Коши и по Гейне. Геометрическая интерпритация.

Функция

Если каждому значению переменной x из множества {x} ставится в соответствие по известному закону некоторое число y, то говорят что на множестве {x} задана функция y= y(x) или y= f(x)

_____________

предел функции по Гейне. imx f(x) =A (x>>a)

Пусть f: X → R и x0 - предельная точка множества X.

(Гейне): Функция f имеет предельное значение при x → x0 (или в точке x0), если существует такое число , что для произвольной последовательности (xn) значений , сходящейся к точке x0, соответствующая последовательность значений функции (f(xn)) сходится к точке A.

предел функции по Коши. Число A  R называется пределом функции f(x) в точке a или при x>> a и это обозначается следующим образом limx f(x) = A (x>>a), если

При этом число A называем пределом (или предельным значением) функции f в точке x0 и записываем

или f(x) → A при x → x0.

________________________

Предел функции

Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности {Xn} такой, что сходящейся к числу a, соответствующая последовательность значений функции сходится к числу A.

17 Предел функции на бесконечности и бесконечный предел. Односторонние пределы.

Односторонние пределы. Если в определении предела функции по Гейне наложить на последовательность Х_{n ,} условие X_n > a (Х_n< a) вместо условия Х_n а, то мы получим определение правого (левого) предела y=f(x) , который обозначается f(x) ( f(x)).

Пример. Функция y=sign x имеет в нуле правый и левый пределы: sign x=+1

sign x= -1

В самом деле, если X_n – любая сходящаяся к нулю последовательность значений аргумента, элементы которой больше нуля (X_n >0) , то sign X_n = 1 и поэтому sign X_n =1. Таким образом, sign x=1. Аналогично доказывается, что = -1. Отметим, что вместо 0+0(0-0) иногда пишут 0+(0-) или +0(-0).

Предел функции в бесконечности. Запись f(x)=b означает, что для всех достаточно больших по абсолютной величине значений x значения функции отличаются от b достаточно мало. Строгое определение предела в бесконечности выглядит следующим образом.

Определение. Число b называется пределом функции y=f(x) при x , если для любого >0 найдется D>0 такое, что для всех x , удовлетворяющих неравенству |x| >D, выполняется неравенство: | f(x) – b| < .

Если в данном определении потребовать, чтобы значения x были положительны (отрицательны), т.е. заменить условие |x| >D на x>D (x< -D), то мы получим определение предела f(x) ( f(x)). Заметим, что если f(x) = f(x) = b , то f(x)=b.

Пример. Докажем, что 2^-x =0. Для любого фиксированного >0 возьмем D= log₂ 1/ , тогда |f(x)-b| = |2^-x – 0| = 2^-x < 2 ^ (- log₂ 1/ ) = , x>D.

Бесконечные пределы. Запись f(x) = означает, что для всех x , достаточно близких к a, значения функции по абсолютной величине достаточно велики. Ниже приведем строгое определение.

Определение. Предел функции равен бесконечности в точке x=a , если для любого E > 0 найдется такое > 0, что для всех x , удовлетворяющих неравенству 0 < |x-a| < , выполняется неравенство |f(x)| > E.

Если наложить условие f(x) > 0 (f(x)<0), то мы придем к определению предела f(x) = + ( f(x) = - );

В этом случае неравенство |f(x)| > E в данном выше определении заменится на f(x)>E (f(x)< - E)

Пример. Докажем, что ln|x| = - . В самом деле, пусть E >0 – любое фиксированное число; возьмем = e^-E , тогда при |x-0| <

F(x) = ln|x| < ln = -E.

Это означает, что f(x) = - .

Функция, предел которой в данной точке равен называется бесконечно большой в этой точке.

18 Замечательный предел

Предел sin x / x существует и равен единице.

Доказательство. Начнем с обоснования одного неравенства, которое потребуется нам при доказательстве, для чего проведем следующие геометрические построения. На окружности единичного радиуса с центром О возьмем точку А и проведем прямую через О и А, затем отложим угол, равный Х радиан (0<x< ), от вектора OA в положительном направлении (против часовой стрелки) при этом точка A перейдет в точку M. Обозначим также через B точку пересечения касательной в точке A с продолжением прямой OM. Соединим точку A и M отрезком прямой. Вычислим площади трех фигур, изображенных на рисунке1.

Рисунок 1.

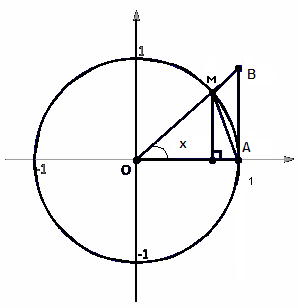
Площадь треугольника OMA равна ½ |OM|*|OA|*sin x = ½ sin x (половина произведения сторон на угол между ними); площадь сектора OMA равна x/2 (половина центрального угла) : площадь треугольника OBA равна ½|OA|*|OB|*sin x = ½*1/cos x * sin x=1/2*tg x.

Фигуры вложены друг в друга, поэтому их площади удовлетворяют неравенствам:

S_OMA <S_сект.OMA<S_OBA, т.е.

½ sin x< x/2<tg x (0< x< ). Умножая эти неравенства на 2, деля на sin x , получаем

1< x/ sin x<1/ cos x.

Наконец, заменяя все части неравенства на обратные величины, имеем

Cos x<sin x / x<1 (0< x< ).

Это же неравенство справедливо и при - <x<0 , в чем легко убедиться, заменив x на – x.

Теперь перейдем собственно к доказательству. Пусть X_n - произвольная последовательность X_n, но такая, что имеем X_n =0, X_n 0 cos X_n < sin X_n / X_n<1.

Пусть n . Докажем, что cos X_n =1. Используя формулу 1-cos = 2sin² /2 и неравенство |sin t|<=t, справедливо для любых t, имеем

| cos X_n -1| = 2sin² X_n/2 <= 2*( X_n/2 )^2 0,  , следовательно, по теореме о предельном переходе в неравенстве, cos X_n =1.

Теперь в неравенстве cos X_n < sin X_n / X_n<1 устремим n . И правая, и левая его части стремятся к 1, поэтому по теореме о трех последовательностях sin X_n / X_n =1.

Поскольку X_n – произвольная, то по определению предела последовательности по Гейне

sin X_n / X_n =1.