3.3. Моделирование процессов диффузии в твердом теле

При высокой концентрации примеси, как в случае диффузии в условиях постоянной поверхностной концентрации, так и в случае диффузии из ограниченного источника, измеряемые профили распределения концентрации примеси отклоняются от рассчитанных согласно уравнениям (3.13). В большинстве случаев профиль распределения примеси в областях с высокой концентрацией может быть описан с помощью концентрационной зависимости коэффициента диффузии. Для определения концентрационной зависимости коэффициента диффузии из экспериментальных данных используют уравнение (3.5).

В этом раз деле, как и в предыдущем, процесс диффузии рассматривается при двух условиях: постоянной поверхностной концентрации диффузанта и постоянном общем числе атомов диффузанта.

Постоянная поверхностная концентрация. Уравнение (3.5)

(3.5)

представляет собой одномерное уравнение диффузии с коэффициентом диффузии, зависящим от концентрации диффузанта. В тех случаях, когда D зависит только от концентрации диффузанта N и поверхностная концентрация поддерживается на постоянном уровне, уравнение (3.5) может быть преобразованно в обычное дифференциальное уравнение с новой переменной

(3.15)

Тогда , , отсюда и .

Подставляем и во второй закон Фика (3.5):

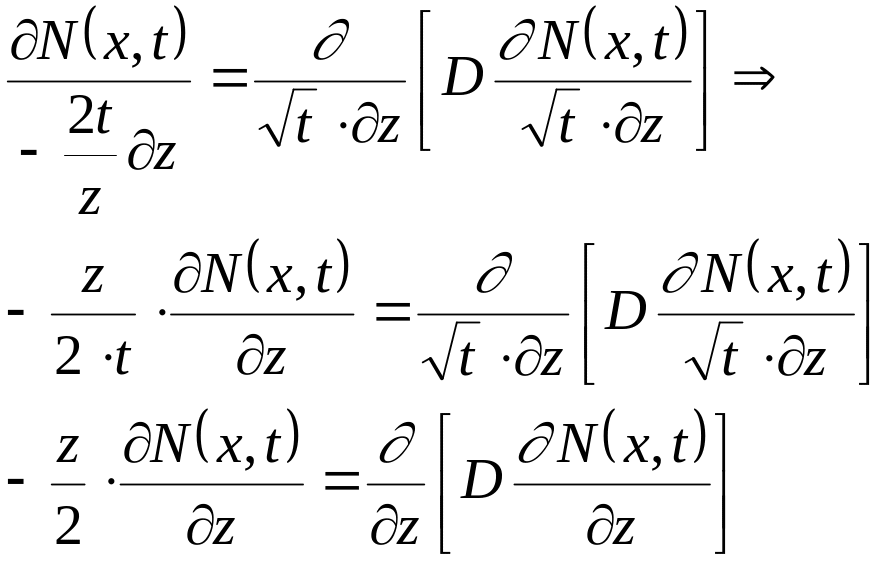(3.16)

Таким образом, как D, так и N зависят явным образом только от x.

Решения уравнений с новыми переменными в рассматриваемых ранее случаях будут выглядеть следующим образом.

3.3.1. Диффузия из одной полуограниченной области в другую

Пусть Распределение примеси имеет следующий вид (рис. 3.3):

Краевые условия для этого случая записываются в следующем виде:

Начальные условия:

при и любых , , а ;

при и любых , , .

Ход вычислений становится более прозрачным, если временно ввести новую переменную . Тогда (3.16) перепишется в форме, соответствующей уравнению с разделяющимися переменными.

, (3.17)

которое можно записать в виде:

(3.18)

Интеграл этого выражения равен

(3.19)

или

(3.20)

З

Рис. 3.3. Распределение примеси при диффузии из одной полуограниченной области в другую

десь C₁ и C₂ - это просто две разных записи для одной и той же постоянной интегрирования. Из (3.20) очередным интегрированием получается:

(3.21)

Произведена замена переменной , а множитель 2 при C₂ включен в состав постоянной интегрирования С₄.

Оставшиеся постоянные интегрирования С₃ и С₄ нужно определять с учетом начальных и краевых условий. Рассмотрим значение интеграла, _, вычисляемого в пределах от u_o до + ∞.

Если , и , и, следовательно, С₃=0.

Если , то

, а . (3.22)

Следовательно, .

Таким образом:

(3.23)

В анализировавшемся нами примере область, первоначально не содержавшая примеси, соответствовала положительным значениям аргумента. Если бы она приходилась на его отрицательные значения, то имело бы место соотношение .

Важно отметить, что , так что

.

Таким образом, профиль распределения примеси при диффузии из источника неограниченной мощности обычно записывают в форме

. (3.24)