10 Момент силы

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

Общие сведения

В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:

где  — сила, действующая на частицу, а  — радиус-вектор частицы.

Предыстория

Строго говоря, вектор, обозначающий момент сил, введен искусственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси.

Работа, совершаемая при действии силы на рычаг , совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол dφ. Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол между вектором и вектором силы .

Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .

Теперь попытаемся выразить модуль вектора через радиус-вектор , а проекцию вектора силы на вектор , через угол .

Так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl = rsin dφ, где в случае малого угла справедливо sin dφ = dφ и следовательно

Для проекции вектора силы на вектор , видно, что угол , а так как , получаем, что .

Теперь запишем бесконечно малую работу через новые равенства или .

Теперь видно, что произведение есть не что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуль вектора момента силы .

Теперь полная работа записывается очень просто: 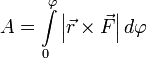или .
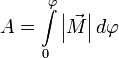