9 Степени свободы (механика)
В механике, степени свободы — это совокупность независимых координат перемещения и/или вращения, полностью определяющая движение и/или положение тела или системы тел. Это фундаментальное понятие применяется в теоретической механике, теории механизмов и машин, машиностроении, авиационной промышленности, робототехнике и других областях.
Примеры
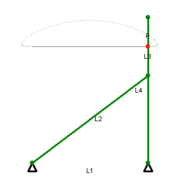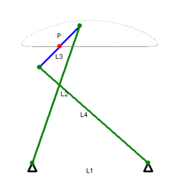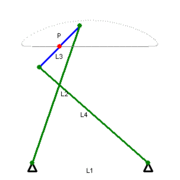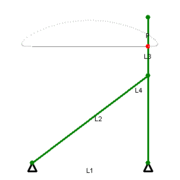
Этот механизм Чебышева имеет только одну степень свободы, так как его положение полностью определяется углом поворота любого из трёх подвижных звеньев — либо L2, либо L3, либо L4.
Твёрдое тело, движущееся в трёхмерном пространстве, максимально может иметь шесть степеней свободы: три поступательных и три вращательных.
Автомобиль, если его рассматривать как твёрдое тело, перемещается по плоскости, а точнее говоря, по некоторой двумерной поверхности (в двумерном пространстве). Он имеет три степени свободы (одну вращательную, и две поступательные).
Поезд вынужден перемещаться по рельсовому пути, и поэтому он имеет только одну степень свободы.
Движение и размерности
В общем случае твёрдое тело в d измерениях имеет d(d + 1)/2 степеней свободы (d поступательных и d(d −1)/2 вращательных).
Упругие или деформируемые тела можно рассматривать как систему множества мельчайших частиц (бесконечное число степеней свободы; в этом случае систему часто приближённо рассматривают как имеющую ограниченное число степеней свободы.
Если основным объектом анализа является движение, вызывающее большие перемещения (например, движение спутников), то для упрощения расчётов деформируемое тело приближённо рассматривают как абсолютно твёрдое.
Системы тел
Система из нескольких тел может иметь в целом такое количество степеней свободы, которое является суммой степеней свободы составляющих систему тел, за вычетом тех степеней свободы, которые ограничиваются внутренними связями. Механизм, содержащий несколько соединённых тел, может иметь количество степеней свободы большее, чем имеет одно свободное твёрдое тело. В этом случае термин «степени свободы» используется для обозначения количества параметров, необходимых для точного определения положения механизма в пространстве.
Специфическим типом механизма является открытая кинематическая цепь, в которой жёсткие звенья имеют подвижные соединения, способные обеспечить одну степень свободы (если это петлевой шарнир или скользящее соединение), или две степени свободы (если это цилиндрическое соединение). Подобные цепи используются в основном в робототехнике, биомеханике и для космических механизмов.
Рука человека имеет 7 степеней свободы.
Робот, имеющий механизм, способный контролировать все 6 физических степеней свободы, называют голономным. Если робот имеет меньшее количество контролируемых степеней свободы, то его называют неголономным. Робот или другой объект с количеством контролируемых степеней свободы бо́льшим, чем количество физических степеней свободы, называют избыточным.
Определение степеней свободы механизмов
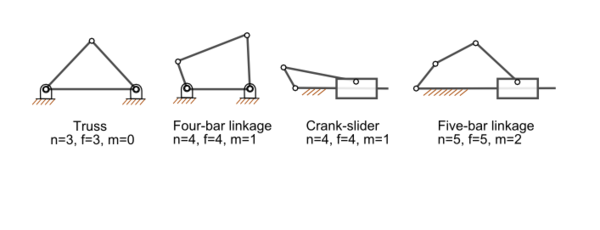
Определение количества степеней свободы плоских механизмов: m — количество степеней свободы; n — количество звеньев механизма (включая одно неподвижное звено); f — количество подвижных соединений звеньев
Большинство обычных механизмов имеют одну степень свободы, то есть, имеется одно входное движение, определяющее одно выходное движение. Кроме того, большинство механизмов являются плоскими. Пространственные механизмы более сложны для расчётов.
Для расчётов степеней свободы механизмов применяется формула Чебышева — Граблера — Кутцбаха (англ.).
В наиболее простом виде для плоских механизмов эта формула имеет вид:
,
где
—
количество степеней свободы;
—
количество звеньев механизма (включая
одно неподвижное звено — основание);
—
количество кинематических
пар с одной степенью свободы
(петлевое
или скользящее
соединение);
В более общем виде формула Чебышева — Граблера — Кутцбаха для плоских механизмов, содержащих более сложные соединения звеньев:
,
где
Или для пространственного механизма (механизма, имеющего трёхмерное движение):
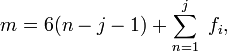
— количество степеней свободы;
— количество звеньев механизма (включая одно неподвижное звено — основание);
—
общее количество подвижных соединений
звеньев, не рассматривая количество
степеней свободы этих соединений;
—
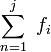сумма всех степеней свободы всех
подвижных соединений (шарниров).
Число степеней свободы - это число независимых величин, которые необходимо задать для того, чтобы однозначно определить положение тела в пространстве. В разных ситуациях число степеней свободы твердого тела может быть различным.Твердое тело имеет шесть степеней свободы, как бы ни было велико число N образующих его точек.