Вязкость жидкостей Динамический коэффициент вязкости

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона:

Коэффициент вязкости η (динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что η будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде:

η = Ce^{w / kT}

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества V_M. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение

где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.

Динамическая вязкость жидкостей уменьшается с увеличением температуры, и растёт с увеличением давления.

Кинематическая вязкость

В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной

и эта величина получила название кинематической вязкости. Здесь ρ — плотность жидкости; η — динамическая вязкость (см. выше).

Кинематическая вязкость в старых источниках часто указана в сантистоксах (сСт). В систему СИ эта величина переводится следующим образом:

1 сСт = 1мм² / 1c = 10 ^{− 6} м² / c

Ньютоновские и неньютоновские жидкости

Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. В уравнении Навье — Стокса для ньютоновской жидкости имеет место аналогичный вышеприведённому закон вязкости (по сути, обобщение закона Ньютона, или закон Навье):

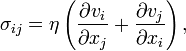
где σ_i,j — тензор вязких напряжений.

Среди неньютоновских жидкостей, по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.

С повышением температуры вязкость многих жидкостей падает. Это объясняется тем, что кинетическая энергия каждой молекулы возрастает быстрее, чем потенциальная энергия взаимодействия между ними. Поэтому все смазки всегда стараются охладить, иначе это грозит простой утечкой через узлы.

Относительная вязкость

В технических науках часто пользуются понятием относительной вязкости, под которой понимают отношение коэффициента динамической вязкости (см. выше) раствора к коэффициенту динамической вязкости чистого растворителя:

где μ — динамическая вязкость раствора; μ₀ — динамическая вязкость растворителя.

26

Ламинарный и турбулентный режим течения жидкости

Знаменитый русский ученый Д. И. Менделеев в своем сочинении «О сопротивлении жидкостей и о воздухоплавании» в 1880 г. указывал на существование в природе двух режимов движения жидкости с различными законами ее сопротивления. Эта же мысль была развита и доказана в 1883 г. русским физиком Н. П. Петровым (1836—1920), впервые установившим, что при смазке силы трения, определяемые вязким сопротивлением при ламинарном движении, пропорциональны первой степени скорости. Петрову принадлежат также доказательство гипотезы Ньютона о силе внутреннего трения в жидкостях и разработка гидродинамической теории смазки.

Несколькими годами позже английский ученый Рейнольде провел свои опыты, наглядно подтверждавшие гипотезу Менделеева о существовании ламинарного и турбулентного движения жидкости.

Имеют место два различных по своему характеру режима движения жидкости: ламинарный и турбулентный.

При ламинарном режиме жидкость движется слоями без поперечного перемешивания, причем пульсации скорости и давления отсутствуют.

При турбулентном режиме слоистость нарушается, движение жидкости сопровождается перемешиванием и пульсациями скорости и давления.

Критерием для определения режима движения является безразмерное число Рейнольдса. Для труб круглого сечения число Рейнольдса определяется по формуле:

Re = υ·d/ν;

- для потоков произвольного поперечного сечения

Re_Rг = υ·R_г /ν;

или

Re_Rг = υ·D_г /ν;

где υ — средняя скорость жидкости; d — диаметр трубы; R_г — гидравлический радиус; D_г — гидравлический диаметр; ν — кинематический коэффициент вязкости жидкости.

Режим будет ламинарным, если

Re < Re_кр;

Re_R < Re_Rкр,

 

и турбулентным, если

Re > Re_кр;

Re_R > Re_Rкр,

В выражениях приведенных выше Re_кр и Re_Rкр — критические числа Рейнольдса, для круглых труб обычно принимаемые равными соответственно 2320 и 580. В таблице приведены ориентировочные значения Re_кр для некруглых каналов и некоторых гидроагрегатов, при этом число Рейнольдса определено по формуле Re_Rг = υ·D_г /ν.

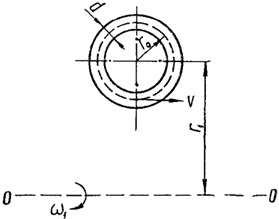
Для изогнутых каналов (витков), вращающихся вокруг внешней оси 0—0 (следующий рисунок), согласно исследованиям Ю. В. Квитковского и К. И. Толчеева, критическое число Рейнольдса получается несколько большим, чем для прямых труб.