
- •1 Основные кинематические величины
- •2 Движение по окружности
- •3 Криволинейное движение
- •4 Законы Ньютона
- •Первый закон Ньютона
- •Современная формулировка
- •Историческая формулировка
- •Второй закон Ньютона
- •Современная формулировка
- •Историческая формулировка
- •Третий закон Ньютона
- •Современная формулировка
- •Историческая формулировка
- •Комментарии к законам Ньютона Сила инерции
- •Законы Ньютона и Лагранжева механика
- •Решение уравнений движения
- •5 Принцип независимости действия сил
- •Момент импульса в классической механике
- •Определение
- •Вычисление момента
- •8 Центр масс
- •Определение
- •Центры масс однородных фигур
- •В механике
- •Центр масс в релятивистской механике
- •Центр тяжести
- •9 Степени свободы (механика)
- •Примеры
- •Движение и размерности
- •Системы тел
- •Определение степеней свободы механизмов
- •10 Момент силы
- •Общие сведения
- •Предыстория
- •Единицы
- •Специальные случаи Формула момента рычага
- •Определение
- •Вычисление момента
- •Сохранение углового момента
- •11 Динамика твердого тела
- •***Можно не читать!***Динамика твердого тела
- •12 Момент инерции
- •Теорема Гюйгенса-Штейнера
- •Осевые моменты инерции некоторых тел
- •Центральный момент инерции
- •13 Теорема Штейнера
- •Работа силы
- •15 Работа - потенциальная сила
- •Работа силы (сил) над одной точкой
- •Работа силы (сил) над системой или неточечным телом
- •Кинетическая энергия
- •История
- •Физический смысл
- •Физический смысл работы
- •Релятивизм
- •Соотношение кинетической и внутренней энергии
- •Потенциальная энергия
- •О физическом смысле понятия потенциальной энергии
- •Физическая абстракция
- •Абсолютно упругий удар
- •Абсолютно неупругий удар
- •Реальный удар
- •Гидростатическое давление
- •Дифференциальное уравнение Бернулли
- •Сила вязкого трения
- •Вторая вязкость
- •Вязкость жидкостей Динамический коэффициент вязкости
- •Кинематическая вязкость
- •Ньютоновские и неньютоновские жидкости
- •Относительная вязкость
- •Ламинарный и турбулентный режим течения жидкости
- •Вязкость. Ламинарные и турбулентные режимы течения
- •Траектория материальной точки
- •Описание траектории
- •Связь со скоростью и нормальным ускорением
- •Связь с уравнениями динамики
- •Траектория свободной материальной точки
- •Движение под действием внешних сил в инерциальной системе отсчёта
- •Движение под действием внешних сил в неинерциальной системе отсчёта
- •Сила инерции
- •Терминология
- •Реальные и фиктивные силы
- •Эйлеровы силы инерции
- •Ньютоновы силы инерции
- •Д’Аламберовы силы инерции
- •Сила инерции на поверхности Земли
- •Силы Второй закон Ньютона
- •Третий закон Ньютона
- •Движение в инерциальной со
- •Движение в неинерциальной со
- •Общий подход к нахождению сил инерции
- •Движение тела по произвольной траектории в неинерциальной со
- •Работа фиктивных сил инерции
- •Существование инерциальных систем отсчёта
- •Эквивалентность сил инерции и гравитации
- •Принцип относительности
- •История
- •Специальная теория относительности
- •Создание сто
- •Основные понятия и постулаты сто
- •Основные понятия
- •Синхронизация времени
- •Линейность преобразований
- •Согласование единиц измерения
- •Изотропность пространства
- •Принцип относительности
- •Постулат постоянства скорости света
- •***Более простой вариант*** Постулаты Специальной Теории Относительности (сто)
- •Преобразования Лоренца
- •Преобразования Лоренца в физике
- •Вид преобразований при коллинеарных (параллельных) пространственных осях
- •Вывод преобразований
- •Разные формы записи преобразований Вид преобразований при произвольной ориентации осей
- •Преобразования Лоренца в матричном виде
- •Свойства преобразований Лоренца
- •Следствия преобразований Лоренца Изменение длины
- •Относительность одновременности
- •Замедление времени для движущихся тел Связанные определения
- •История
Определение
Момент импульса частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
где — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, — импульс частицы.
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
где — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как где - импульс бесконечно малого точечного элемента системы).
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.
Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:
.
Замечание: в принципе момент импульса может быть вычислен относительно любого начала отсчета (получившиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определенности) его вычисляют относительно центра масс или закрепленной точки вращения твердого тела итп).
Вычисление момента
Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам и . Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения. Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на неё можно указать ряд рецептов в соответствии с общими правилами нахождения векторного произведения двух векторов.
где — угол между и , определяемый так, чтобы поворот от к производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения. Направление поворота важно при вычислении, так как определяет знак искомой проекции.
Запишем в виде , где — составляющая радиус-вектора, параллельная вектору импульса, а — аналогично, перпендикулярная ему. является, по сути, расстоянием от оси вращения до вектора , которое обычно называют «плечом». Аналогично можно разделить вектор импульса на две составляющие: параллельную радиус-вектору и перпендикулярную ему . Теперь, используя линейность векторного произведения, а также свойство, согласно которому произведение параллельных векторов равно нулю, можно получить еще два выражения для .
Сохранение углового момента
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная момента импульса по времени есть момент силы:
![]()
Таким образом, требование замкнутости системы может быть ослаблено до требования равенства нулю главного (суммарного) момента внешних сил:
![]()
где
![]() —
момент одной из сил, приложенных к
системе частиц. (Но конечно, если внешние
силы вообще отсутствуют, это требование
также выполняется).
—
момент одной из сил, приложенных к
системе частиц. (Но конечно, если внешние
силы вообще отсутствуют, это требование
также выполняется).
Математически
закон сохранения момента импульса
следует из изотропии
пространства, то есть из инвариантности
пространства по отношению к повороту
на произвольный угол. При повороте на
произвольный бесконечно малый угол
![]() ,
радиус-вектор частицы с номером
,
радиус-вектор частицы с номером
![]() изменятся
на
изменятся
на
![]() ,
а скорости —
,
а скорости —
![]() .
Функция Лагранжа
.
Функция Лагранжа
![]() системы
при таком повороте не изменится,
вследствие изотропии пространства.
Поэтому
системы
при таком повороте не изменится,
вследствие изотропии пространства.
Поэтому

С
учетом
![]() ,
где
,
где
![]() —
обобщенный импульс
-той
частицы, каждое слагаемое в сумме из
последнего выражения можно переписать
в виде
—
обобщенный импульс
-той
частицы, каждое слагаемое в сумме из
последнего выражения можно переписать
в виде
![]()
Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:
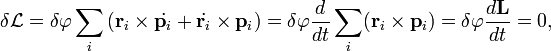
где,
![]() —
момент импульса системы. Ввиду
произвольности δφ, из равенства
—
момент импульса системы. Ввиду
произвольности δφ, из равенства
![]() следует
следует
![]() .
.
На орбитах момент импульса распределяется между собственным вращением планеты и момента импульса ее орбитального движения:
![]()
