2.2. Метод Якова-Бернулли

Будем искать решение уравнения yʹ+ P(x) y=Q(x) в виде произведения двух функций y=uv, где u=u(x), v=v(x)-непрерывные ф-ции

Подберем такие функции u=u(x) и v=v(x), чтобы их произведение удовлетворяло исходному уравнению, т.е. превращало бы его в тождество.

Подставим в уравнение y=uv, yʹ=uʹv+ uvʹ:

uʹv+ uvʹ+Р(х)uv= Q(x)

или

uʹv+ u(vʹ+Р(х)v)= Q(x)

Выберем функцию v такой, чтобы vʹ+Р(х)v=0 из чего автоматически следует, что uʹv= Q(x)

Эти два условия превращают уравнение в тождество, поэтому для решения уравнения достаточно решить простую систему двух дифференциальных уравнений с разделяющимися переменными:

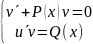
Решая первое уравнение системы, найдем функцию v (при интегрировании будем считать С = 0).

Подставив во второе уравнение системы найденную функцию v=v(x), решим дифференциальное уравнение с разделяющимися переменными относительно u, общее решение которого u=u(x,С). Следовательно, искомое общее решение уравнения будет иметь вид: y=v(x)u(x,С).

Замечание. В ряде случаев дифференциальное уравнение первого порядка является линейным не относительно у, а относительно х, т.е. имеет вид: dy/dx+ P(у) х= Q(x)

Для интегрирования такого уравнения используется описанный выше метод, где неизвестной функцией является х=х(у)

Ду с разделяющимися переменными и его решение.

О. Уравнением с разделяющимися переменными называется уравнение вида yʹ=f₁(x) f₂(у), где правая часть уравнения есть произведение функции, зависящей только от х, на функцию, зависящую только от у. (ф-ции f₁(x) f₂(у)-непрерывные)

Схема интегрирования такого уравнения:

1. Представим производную искомой функции в виде yʹ=dy/dx :

dy/dx= f₁(x) f₂(у)

2. Умножим обе части уравнения на dx:

dy = f₁(x) f₂(у) dx

3. Разделим переменные, поделив обе части уравнения на f₂(у) ≠0, выражения, содержащие y расположим влевой части неравенства, а х-в правой. :

(1/ f₂(у) ) dy = f₁(x) dx

4. Интегрируем обе части. Равенство (1/ f₂(у) ) dy = f₁(x) dx можно рассматривать как равенство двух дифференциалов, а неопределенные интегралы от них будут отличаться постоянным слагаемым. (*м.б. C) Интегрируя левую часть по у, а правую по х, получим: ∫(1/ f₂(у) ) dy = ∫f₁(x) dx

Это соотношение связывает искомую функцию y, независимую переменную x и произвольную постоянную С, т.е. является общим интегралом уравнения yʹ=f₁(x) f₂(у),

*у явл-ся функцией х, если каждому допустимому значению х соотв единств значение у

Ду второго порядка, его общее и частное решение. Простейшее ду второго порядка и его решение.

Простейшим дифференциальным уравнением 2-го порядка называется уравнение вида yʹʹ= f(x)

Его общее решение можно получить с помощью 2 последовательных интегрирований:

y^(n-1)=уʹ= ∫f(x)dx+C₁= f₁(x) +C₁

y^(n-2)=у= ∫(f(x)dx+C₁)dx=∫f₁(x)dx+ C₁∫dx= f₂(x) +C₁x+C₂

Получим общее решение уравнение, в котором количество произвольных постоянных равно порядку уравнения. С₁ и С₂=n=2

Частным реш-ем д.у. 2-ого порядка называется любая функция, полученная из общего решения д.у. при конкретных значениях произвольных постоянных.

Найти общее решение уʹʹ=cosx

yʹ=∫cosxdx=sinx+C₁

y=∫(sinx+C₁)dx=-cosx+C₁x+C₂

*если бы в условии задачи были данные у(а)=b, где у=b при х=а, то мы бы нашли и частное решение данного д.у. 

ДУ ВТОРОГО ПОРЯДКА, ДОПУСКАЮЩЕЕ ПОНИЖЕНИЕ ПОРЯДКА

1. уʹʹ= f(x)

уʹ=z(x)=z

zʹʹ=zʹ(x)=zʹ

zʹ=f(x)

dz/dx=f(x)

∫dz=∫f(x)dx

z=∫f(x)dx+C₁

уʹ=z

yʹ=∫f(x)dx+C₁

dy/dx=∫f(x)dx+C₁

dy=(∫f(x)dx+C₁)dx+Cdx

у=∫f(x)dx+C₁∫dx+C₂

2. уʹʹ= f(уʹ,x)

уʹʹ+(2/х)уʹ=0

*Вот у этого примера также можно понизить порядок

уʹ=z → уʹ=zʹ

zʹ+(2/х)z=0

*А вот был бы у мы бы так сделать не смогли 

zʹ=-(2/х)z

dz:dx=-(2/х)z

dz:z=-(2/х)dx

∫dz:z=-∫(2/х)dx

Ln|z|=-2ln|x|+ln|C|

z=±C₁:x²

±C₁=C₂

z=C₂:x²

уʹ= C₂:x²

dy/dx= C₂:x²

∫dy=∫( C₂:x²)dx

Y=C₂∫ x-²dx

Y=-C₂:x+C₃