1. Дисперсия

2. Среднее квадратическое отклонение

Стандартное отклонение

Дисперсия-мат ожидание квадрата центрированной СВ

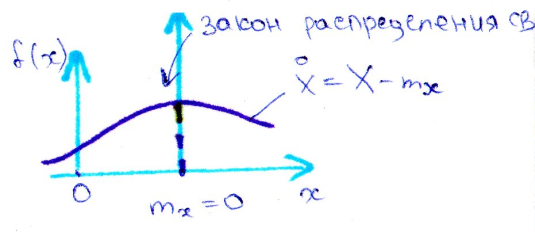
Центрированная СВ-СВ у кот начало отсчета помещено в точку мат ожидания

D_x=M[x^o2]=M[(X-m_x)²]= ]=(сверху n, снизу i=1)(x_i-m_x)²p_i *Дисперсия равна сумме произведений(для дискретных величин)

Для непрерывных СВ формула:

D_x=∫(сверху +∞, снизу -∞)(х-m_x)² f(x)dx

Выведем рабочую формулу для рассчета дисперсии (более простую):

Дисперсия равна интегралу бесконечного предела:

D_x=∫(сверху +∞, снизу -∞)( х-m_x)² f(x)dx=∫(сверху +∞, снизу -∞)(x²-2m_x*x+m_x²) f(x)dx=∫(сверху +∞, снизу -∞)(x²) f(x)dx-(2m_x) ∫(сверху +∞, снизу -∞)(x)f(x)dx+(m_x²) ∫(сверху +∞, снизу -∞)f(x)dx=∫(сверху +∞, снизу -∞)(x²) f(x)dx-2m_xm_x+ m_x²=∫(сверху +∞, снизу -∞)(x²) f(x)dx-m_x²=∫(сверху +∞, снизу -∞)(x-0)² f(x)dx-m_x²= M[x²]-m²_x

D_x=M[x²]-m²_x *мат ожидание квадрата СВ минус квадрат мат ожидания

Среднее ожидание СВ-размерность СВ

Т.к. Размерность дисперсных величин-квадрат СВ, пользоваться ею на практике неудобно 

Поэтому на практике выведена еще одна хар-ка рассеивания СВ- среднее квадратическое отклонение.

σ_х=√ Dx – корень из дисперсии СВ

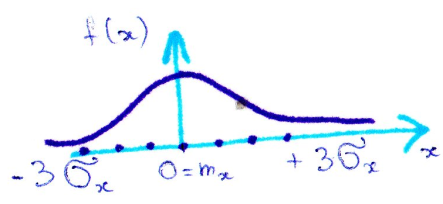
установлено что 99,7% всех значений СВ укладываются в предел +/- 3σ_х – ПРАВИЛО ТРЕХ СИГМ

Пример:

Х	1	2	4	5
pi	0,28	0,1	0,32	0,3

Найти:

1. M[x]

2. D_x

3. σ_х

Решение:

1. Расчетная формула: M[x]=(сверху n, снизу i=1)x_i*p_i -дискретная СВ

Проведение расчетов: M[x]=1*0,28+2*0,1+4*0,32+5*0,3=3,26

2. D_x=M[x²]-m²_x

m²_x =3,26*3,26=10,6

M[x²]= 1²*0,28+2²*0,1+4²*0,32+5²*0,3=13,3

D_x=13,3-10,6=2,7

3. σ_х=√ Dx=√2,7=1,6

Дискретные СВ.

Пример:

1. Рассматривется работа 3х независимо работающих технических устройств.Вероятность норм работы 1ого-0,2, второго-0,4, третьего 0,5. Построить функцию распределения СВ X – числа работающих устройств.

1. Обозначение событий и их вероятностей.

А-событие состоящее в норм работе первого устройства.

Р(А)=0,2

В- -//- Р(В)=0,4

С- -//- Р(С)=0,5

2. Построение ряда распределения

Х:х₁=0, х₂=1, х₃=2, х₄=3 – кол-во работающих устройств.

Рассчитываем отвечающим данным значениям случ величины вероятностей.

1. х₁=0

Р(Х=х₁)=Р(х=0)=0,24

D-не раб ни один прибор.

А(сверху -) – противоп событие

D=A*B*С(все три буквы с черточкой сверху)

*вероятность событий=произведению их вероятностей.

Р(D)=P(A с черточкой)* P(В с черточкой)* P(С с черточкой)=(1-0,2)*(1-0,4)*(1-0,5)=0.24

2. х₂=1

Е-событие в том что работает один прибор.

Е= A*B*С+ A*B*С+ A*B*С(в каждом умножении две буквы с черточкой,а одна нет)

Р(Е)=P(A)* P(В с черточкой)* P(С с черточкой)+ P(A с черточкой)* P(В)* P(С с черточкой)+ P(A с черточкой)* P(В с черточкой)* P(С )

P(С)=0,2*0,6*0,5=0,8*0,4*0,5+0,8*0,6*0,5=0,46

Р(Х=х₂)=Р(х=1)=0,46

3. х₃=2

К-событие что раб 2 прибора

Р(К)= P(A)* P(В)* P(С с черточкой)+ P(A с черточкой)* P(В)* P(С)+ P(A)* P(В с черточкой)* P(С )=0,26

Р(Х=х₃)=Р(х=2)=0,26

4. х₄=3

F=АВС=0,2*0,4*0,5=0,04

Проверка: х₁₊х₂₊х₃₊х₄=1

Сроим ряд распределения:

Х	0	1	2	3
Р	0,24	0,46	0,26	0,04

По оси х значения 0,1,2,3,4

По оси у (снизу вверх): 0,24 0,5 0,7 0,96

1. Х=х₁=0

F(X=0)=F(0)=P(x<0)=0

2. Х=х₂=1

F(X=1)=F(1)=P(x<1)=0+0,24=0,24

3. Х=х₃=2

F(X=2)=F(2)=P(x<2)=0,24+0,46=0,7

4. Х=х₄=3

F(X=3)=F(3)=P(x<3)=0,7+0,26=0,96

5. X>3

F(X>3)= P(x=0)+ P(x=1)+ P(x=2)+ P(x=3)=0,24+0,46+0,26+0,04=1