22. Непрерывность дифференцируемой функции

Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция fнепрерывна на (a, b).

Доказательство

Возьмем произвольное фиксированное число x   (a,b).

По условию теоремы

Следовательно, в малой окрестности числа x₀ можно определить функцию α = α(Δx), стремящуюся к нулю при   такую, что

Но тогда   и, следовательно, функция f непрерывна при x = x₀. Так как число x₀ – произвольное, то функция f непрерывна на всем интервале (a, b). Из доказанной теоремы непосредственно вытекает, что в точках разрыва функция не может быть дифференцируемой.

23. Производная и дифференцируемость функции в точке

Пусть в некоторой окрестности точки   определена функция  Производной функции f в точке x₀ называется предел, если он существует,

Производная функции y = f(x) в точке x₀ обозначается символами

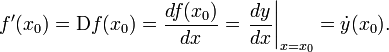
Рассмотрим приращение функции   в точке   

Поведение этого приращения, как функции приращения аргумента   при фиксированном  , показывает, существует ли производная в этой точке у функции  . В случае существования производной   приращение   может быть записано в виде (см. (7.1.1)): 

Если же приращение функции   в точке   может быть записано в виде 

то функция   называется дифференцируемой в точке  . Докажем, что если функция имеет производную в точке  , то она дифференцируема в ней.

Функция   имеет производную в точке   тогда и только тогда, когда она дифференцируема в этой точке.

Доказательство. Необходимость доказана выше.

Достаточность. Рассмотрим  . По определению   имеем 

Отсюда следует, что при наличии дифференцируемости функции   в точке   главную роль в приращении   играет линейная часть . Она называется дифференциалом функции   в точке   и обозначается 

Здесь 

Замечание 7.2.1. Если функция задана в виде  , то и приращение ее, и дифференциал можно записать так: 

24. Дифференцируемость функции в точке: правила дифференцирования, дифференцируемость сложной функции

Пусть задана сложная функция  ; функция   имеет производную в точке  , а функция   имеет производную в точке  . Тогда функция   имеет производную в точке   и 

Доказательство. Так как функция   дифференцируема в точке  , то 

где   при  . Если положить  , то функция   непрерывна в точке  .

Придадим переменной   в точке   малое приращение  ; оно влечет приращение зависимой переменной  :  . Итак, 

Разделив на  , получим 

Так как существует  , то функция   непрерывна в точке   и, следовательно,   при  , и так как , то функция   непрерывна в точке  . Отсюда сложная функция, как суперпозиция непрерывных функций  , непрерывна в точке  .

Теперь, переходя к пределу в (7.3.1) при  , получим 

Правила дифференцирования

Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) ' = 0, (cu) ' = cu';

2) (u+v)' = u'+v';

3) (uv)' = u'v+v'u;

4) (u/v)' = (u'v-v'u)/v^2;

5) если y = f(u), u = (x), т.е. y = f((x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций  и f, то  , или

;

6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем    ≠ 0, то  .

Таблица производных 

На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.

1. (u^)' =  u^1 u' ( принадлежит R¹ ) 2. (a^u)' = a^u lna u'.

3. (e^u)' = e^u u'. 4. (log_a u)' = u'/(u ln a).

5. (ln u)' = u'/u. 6. (sin u)' = cos u u'.

7. (cos u)' = - sin u u'. 8. (tg u)' = 1/ cos²u u'.

9. (ctg u)' = - u' / sin²u. 10. (arcsin u)' = u' / .

11. (arccos u)' = - u' / . 12. (arctg u)' = u'/(1 + u²).

13. (arcctg u)' = - u'/(1 + u²).