Контрольные вопросы к пп. 1.1. И 1.2

1. Цель и суть любой дискретизации.

2. Представление сигналов функциями; понятие квантованного по уровню сигнала.

3. Цель и суть квантования сообщений по уровню; функции АЦП.

4. Определения неравномерного и равномерного квантования, уровней, порогов, шага и шума квантования.

5. Три способа квантования и соответствующая им величина шума квантования.

6. Структуры систем передачи сообщений:

• системы, передающей непрерывный сигнал квантованными сообщениями;

• системы, передающей квантованные сообщения;

• системы, передающей дискретные сообщения в форме квантованных по уровню сигналов.

7. От чего зависит и как оценивается эффективность работы этих систем?

8. Типы (модели) помех.

9. Влияние помех на квантованный по уровню сигнал.

10. Какие факторы определяют величину шага квантования для каждой системы; каково влияние этих факторов?

11. Чем ограничено минимальное значение ошибки восстановления сигнала?

1. Временная дискретизация сообщений. Спектральное и импульсное представление сигналов

Переход от функции непрерывного аргумента к функции дискретного аргумента может быть выполнен путем взятия отсчетов функции в определенные (дискретные) моменты времени. В результате дискретизации исходная непрерывная по аргументу функция заменяется совокупностью ее мгновенных значений. Полученная последовательность узких импульсов называется гребенчатой или решетчатой функцией. По значениям решетчатой функции можно восстановить исходную функцию с некоторой погрешностью.

Непрерывный сигнал необязательно представлен функцией временного аргумента, но так как часто им является, то обычно имеют в виду временную дискретизацию, которая различается на равномерную и неравномерную.

Если дискретизация равномерная, то длительность шагов дискретизации одинакова. При неравномерной дискретизации шаг изменяется на интервале определения функции.

Неравномерная или адаптивная - это такая дискретизация, при которой шаг дискретизации приспосабливается к характеру функции на очередном участке ее определения.

При большом числе отсчетов, т.е. малых шагах дискретизации, количество отсчетов функции на участке определения будет большим и точность воспроизведения - высокой. При малом числе отсчетов снижается точность восстановления. Проблема здесь состоит в выборе такого минимального числа отсчетов, которое будет обеспечивать заданную точность отображения исходного сигнала во время его существования T. Частота отсчетов функции, очевидно, связана с шагом дискретизации.

Дискретизация, обеспечивающая заданную точность отображения сигнала минимальным числом отсчетов на данном интервале определения сигнала, называется оптимальной. Если требуется выполнить дискретизацию равномерную и оптимальную, то задача состоит в выборе максимально возможного шага дискретизации, при котором обеспечивается заданная точность отображения исходного сигнала последовательностью отсчетов (узких импульсов), то есть в виде:

t_max=T / n_min, где Т  длительность сигнала; n_min  минимальное число отсчетов.

Устройства, обеспечивающие адаптивную дискретизацию, должны правильно определять величину следующего шага. Для этого требуется прогноз развития сигнала на ближайшее время, что обычно осуществляется путем определения производных сигнала в текущий момент времени. Чем большего порядка производную мы сможем вычислить, тем точнее будет прогноз, однако с увеличением порядка снижается точность определения производной.

Обычно на практике осуществляется равномерная дискретизация, при которой длительность шагов одинакова. Проблему выбора оптимального шага дискретизации решил советский ученый В. А. Котельников, который доказал, что непрерывный сигнал, удовлетворяющий определенным условиям, может быть абсолютно точно отображен бесконечной последовательностью импульсов, взятых с определенным шагом. Фактически он формально доказал, что непрерывный сигнал можно представить дискретным. Однако много раньше, в 1807г., французский математик Ж. Фурье доказал, что непрерывная функция, удовлетворяющая определенным условиям, может быть представлена множеством специфических дискретных компонент - элементарных функций - гармоник. Каждая гармоника является непрерывной функцией непрерывного аргумента. Однако любая выделенная гармоника является отдельной сущностью, отличающейся от другой. В этом смысле гармоники являются дискретными компонентами сигнала.

Все множество гармоник, представляющих данный сигнал, называют спектром сигнала.

Для полного определения n-й гармоники спектра сигнала необходимо знать:

амплитуду (А_n);

фазу или фазовое смещение (_n);

частоту или период (_n - круговая частота, измеряемая в радианах в секунду;

_n = 2f_n , где f_n - частота, измеряемая в герцах;

1/f_n = Т_n - период n-й гармоники спектра);

закон формирования гармоники (sin или cos).

При этом гармоники принято обозначать и описывать в следующем виде

(рис. 1.14): y(t) = A_n sin (_nt + _n); y(t) = A_n cos (_nt+_n ).

При А_n=1 - нормированная гармоника.

П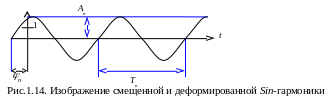 ри А_n1 - деформированная или взвешенная гармоника.

Таким образом, бесконечное множество значений любой гармоники можно компактно отобразить всего тремя информативными параметрами и алгоритмом формирования гармонического сигнала, который принято обозначать символами sin или cos. Ж. Фурье доказал, что сложный непрерывный сигнал представим множеством дискретных элементарных компонент - гармоник, если сигнал является периодическим и удовлетворяет условиям Дирихле, а именно:

1) является однозначным (каждому значению аргумента соответствует только одно значение функции);

2) ограничен по амплитуде;

3) кусочно-непрерывный (нет разрыва даже в одной точке);

4) имеет конечное число экстремумов на интервале определения.

Если не учитывать ограничение на периодичность сигнала, то такая модель сигнала похожа на реальность. При этих условиях исходный непрерывный сигнал может быть представлен следующим рядом:

- ряд Фурье,

где - постоянная составляющая сигнала;

n - номер гармоники в спектре сигнала;

A_n – амплитуда n-ой гармоники спектра;

₀- круговая частота основной или первой гармоники спектра, рад/с,

₀ = 2π/T = 2 f₀;

T - период основной или первой гармоники спектра, c;

f₀ - временная частота основной или первой гармоники спектра, 1/с;

n₀ = _n - круговая частота n-ой гармоники спектра, рад/с;

_n - фаза или фазовое смещение n-ой гармоники спектра (указывает на смещение гармоники относительно начала координат), рад.

Этот ряд принято называть рядом Фурье или обратным преобразованием Фурье.

Математическое высказывание, представленное данным рядом, следует читать и интерпретировать следующим образом. Если известны частоты или периоды, фазовые смещения и амплитуды всех гармоник спектра сигнала и его постоянная составляющая, то можно вычислить значение исходного сигнала для любого момента времени t, просуммировав постоянную составляющую и все множество значений гармоник, вычисленных для данного момента времени.

Р езультат суммирования постоянной составляющей и двух первых гармоник представлен на рис.1.15.

Здесь ₁ = ₂ = /2. При характеристике спектра сигнала различают спектр амплитуд гармоник ( ) - амплитудно-частотную характеристику сигнала (АЧХ) и спектр фаз (_n) – фазочастотную характеристику сигнала (ФЧХ). Эти характеристики показывают распределение амплитуд и фаз по гармоникам спектра в зависимости от их частоты. На основе открытых Фурье спектральных преобразований Котельников доказал, что сложный непрерывный сигнал можно представить в виде следующего ряда:

-ряд Котельникова,

где - нормированная функция отсчетов

(мак симальная амплитуда равна 1; момент существования k-ого отсчета сигнала t^* = k  _T).

_T - шаг дискретизации;

_m - круговая частота высшей гармоники спектра сигнала (самой высокочастотной);

k - номер очередного отсчета сигнала (номер узкого импульса);

t - текущее время.

Данное преобразование, называемое рядом Котельникова, позволяет абсолютно точно отображать сложный непрерывный сигнал последовательностью бесконечно узких импульсов, следующих с равным интервалом (шагом дискретизации), величина которого определяется в виде

, где f_m и T_min - соответственно частота и период высшей гармоники спектра сигнала.

Сигнал, представленный рядом Котельникова, должен удовлетворять следующим условиям:

а) условиям Дирихле;

б) спектр сигнала должен быть ограничен сверху частотой высшей гармоники _m, т.е. частотный диапазон спектра сигнала должен размещаться в пределах (0; _m); гармоник с частотами больше, чем _m не должно быть в спектре данного сигнала.

Нормированные функции отсчетов для разных отсчетных моментов не отличаются по форме, кроме смещения по оси времени (t^* = k  _T , (k + 1)  _T и т. д.) (рис.1.16). Каждая функция отсчетов равняется нулю для всех отсчетных моментов времени, кроме данного.

Для полного определения любой k-ой деформированной функции отсчетов необходимо знать:

значение сигнала в момент k-го отсчета f(k_T);

момент данного отсчета k_T (расположение k-й функции отсчетов на оси времени);

частоту или интервал следования отсчетов _T;

закон формирования функции отсчетов в виде

- деформированная или взвешенная функция отсчетов; f(k_T) - максимальная амплитуда взвешенной функции отсчетов или амплитуда узкого импульса в момент (k_T) k-го отсчета сигнала.

Таким образом, в ряду Котельникова под знаком  расположено множество деформированных функций отсчета. С учетом введенных понятий, математическое высказывание ряда Котельникова представляет исходную непрерывную функцию в любой момент времени t как суперпозицию (сумму) множества деформированных, или взвешенных, функций отсчетов.

Если мы имеем последовательность узких импульсов (решетчатую функцию), полученных путем дискретизации непрерывного сигнала с оптимальным (максимальным) шагом _T, то по этим импульсам можно абсолютно точно восстановить данный сигнал. Процесс восстановления исходной функции имитируется идеальным фильтром нижних частот (ИФНЧ), который отсекает из спектра импульсов все гармоники с частотами выше, чем _m.

Свойства идеального фильтра нижних частот:

1

_m

. АЧХ является прямоугольной, поэтому идеальный фильтр без искажений пропускает на выход гармоники всех нижних частот спектра сигнала и полностью подавляет (срезает) все гармоники с частотами выше, чем _m (рис. 1.17).

2. Если на вход идеального фильтра подают импульс, то ИФНЧ  отсекает из спектра данного импульса все высокочастотные гармоники ( >_m) и размазывает данный импульс во времени до формы, соответствующей его деформированной функции отсчетов. Кроме того, реакции фильтра на последовательность импульсов - деформированные функции отсчетов - суммируются между собой, образуя (восстанавливая) на его выходе непрерывный сигнал сложной формы (как это изображено на рис. 1.18).

1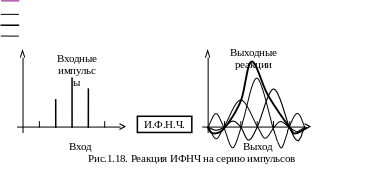 -я функция отсчетов;

2-я функция отсчетов;

сумма трёх функций отсчетов.

3 - я функция отсчетов.

Реальные сигналы имеют конечную длительность и бесконечный спектр, и поэтому не могут быть абсолютно точно восстановлены в промежутках между отсчетными значениями. Оптимальной считается такая дискретизация, которая обеспечивает представление исходной функции с заданной точностью, минимальным количеством отсчетов. В этом случае все отсчеты существенны для восстановления исходной функции.