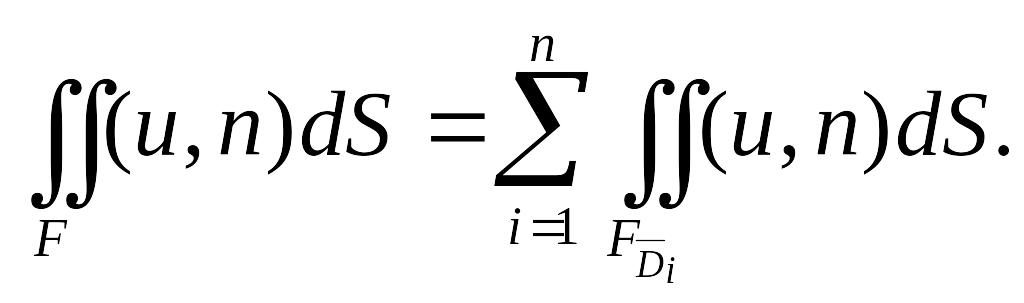19. Длина кривой.

Если кривая задана параметрически , то

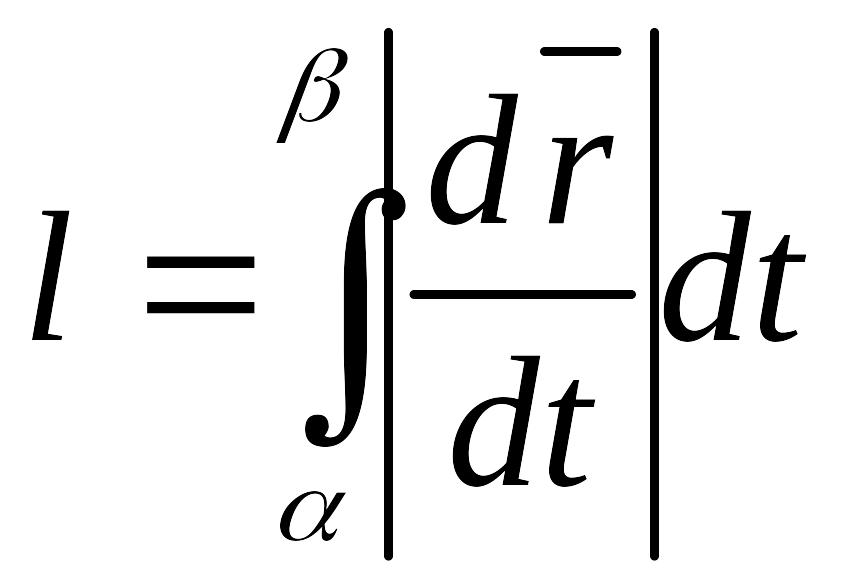
Рассматриваем длину ломаной. Длина ломаной считается так:

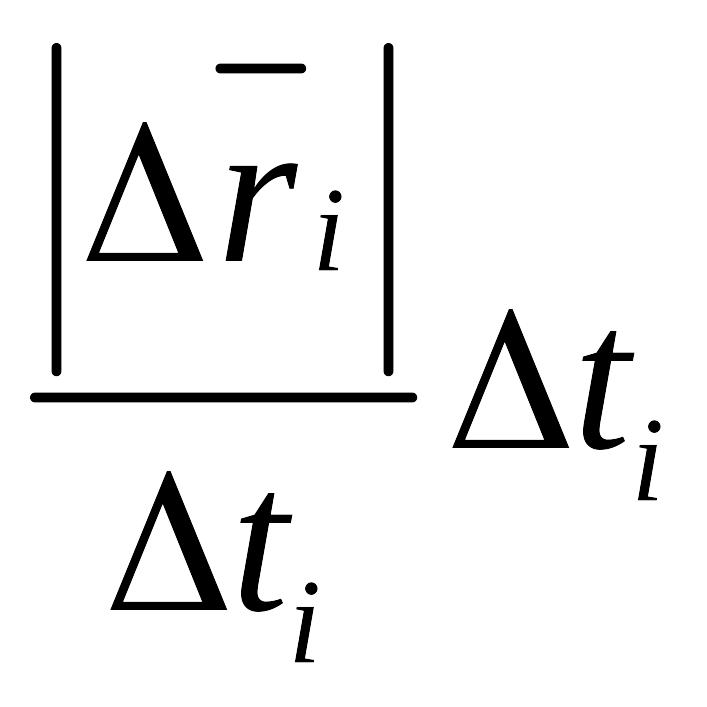если кривая параметризована

Если параметризация такова, что положительна и всё время возрастает, то (в модуль заключили всю дробь):

- длина одного кусочка

- длина ломанной.

Если это непрерывная величина, то сумма стремится к интегралу.

Как считать производную , если мы находимся на поверхности.

Задаём и

Надо определить длину. Для этого определяем квадрат длины и извлекаем корень.

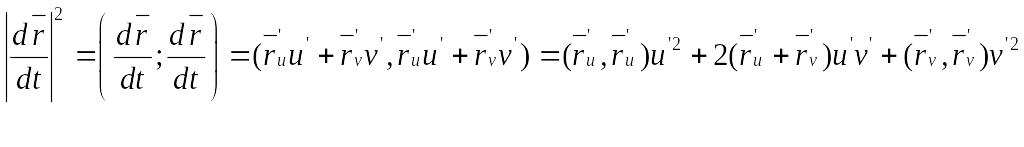Скобки в последнем выражении зависят только от поверхности, а остальное определяется кривой.

Обязанности: 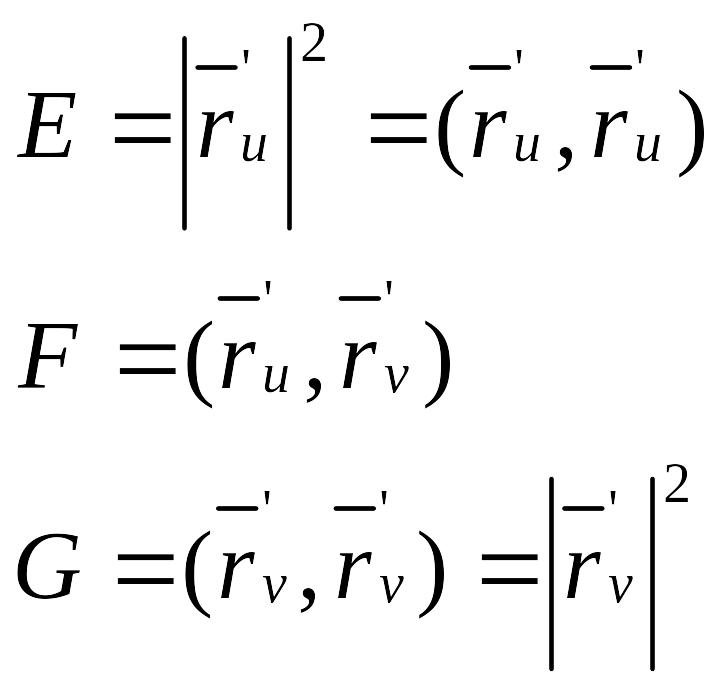тогда:

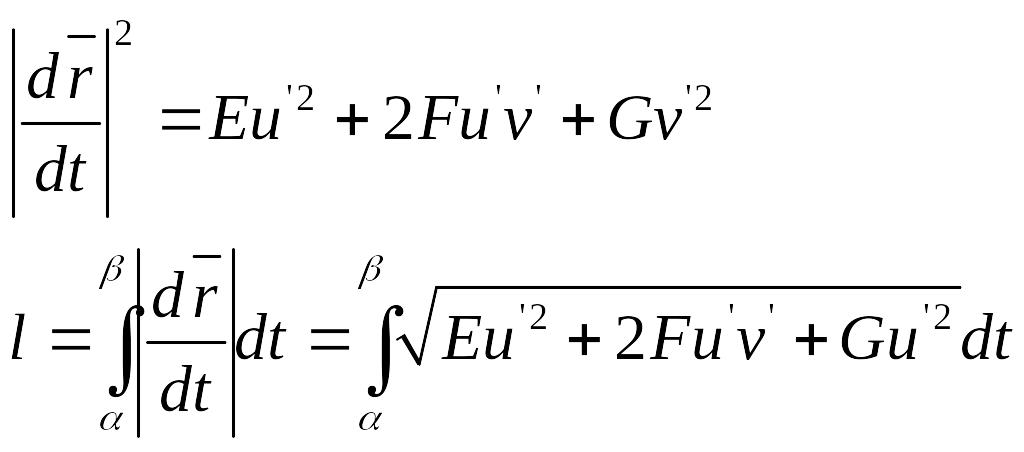
Корень можно извлекать, так как величина под ним должна быть знакоположительная, т.е. или

20. Площадь поверхности.

Пусть F — гладкая регулярная по­верхность без самопересечений, заданная уравнением

;

— замкнутая ограниченная область, граница которой состоит из конечного числа простых замкнутых контуров. Пусть — часть поверхности F, определяемая множеством :

.

Определение. Площадью поверхности называется число

(1)

где Е, F и G — функции, определяемые формулами

Замечания. 1. Под знаком интеграла в формуле (1) стоит площадь параллелограмма, построенного на векторах В самом деле, площадь параллелограмма, построен­ного на векторах как известно, равна

Где — угол между векторами Отсюда следует, - что

т.е.

Следовательно, площадь параллелограмма, построенного на векторах , равна .

2. Если гладкая поверхность F задана уравнением , то

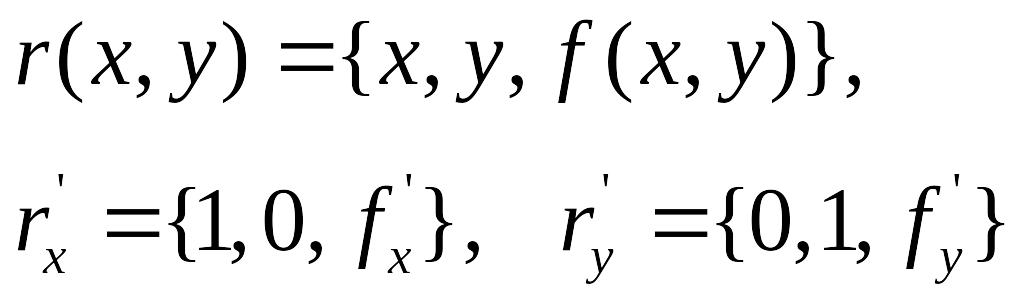
и в силу

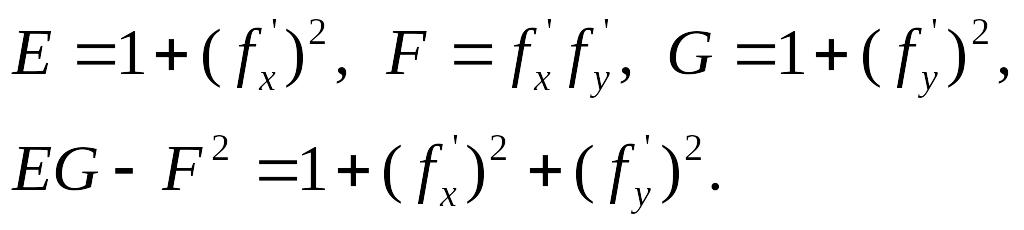
Формула (1) в рассматриваемом случае принимает вид

В частности, если F — координатная плоскость z = 0, то

— площадь замкнутой ограниченной об­ласти .

П

р и м е р. Найдем площадь части сферы радиуса R с центром в начале координат, расположенной в первом октанте,

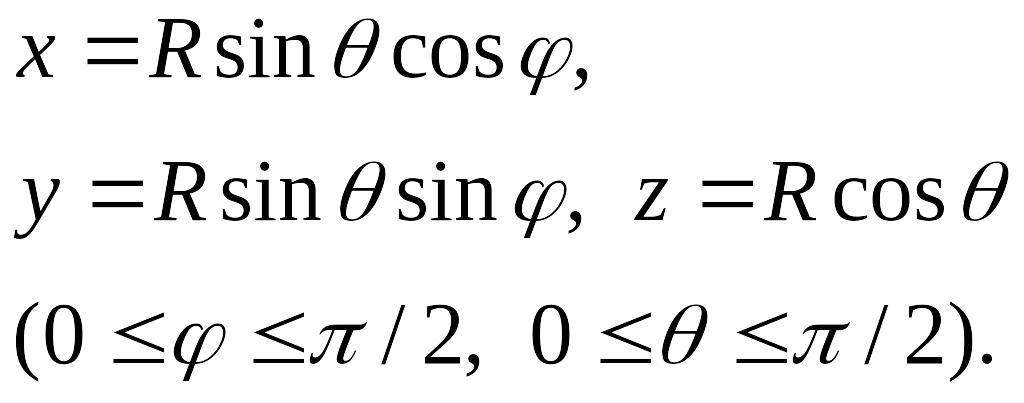
Здесь и — эйлеровы углы .

В данном случае

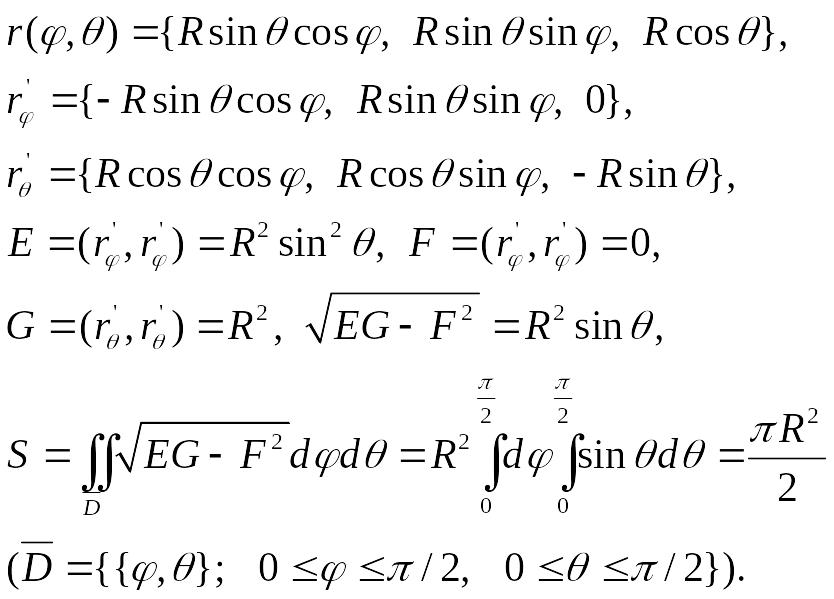
Покажем, что формула (1) инвариантна относительно замены координат и и на поверхности F.

Для этого введем новые координаты и по формулам

- это преобразование и обратное к нему предполагаются непрерывно дифференцируемы. По отношению к новым координа­там поверхность F задается уравнением

где — прообраз замкнутой области при отображении . Имеем следующие соотношения:

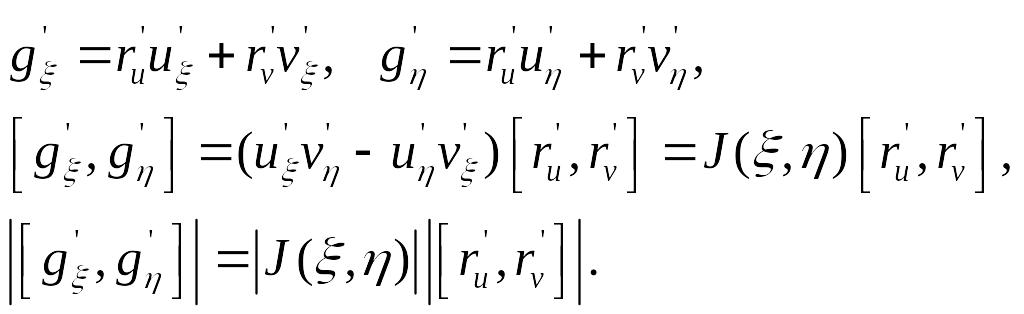
В силу

Где

В двойном интеграле (1) сделаем замену переменных по фор­мулам . Тогда в силу

.

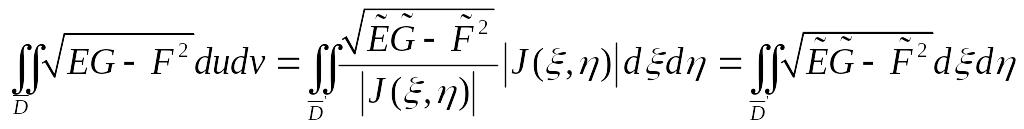Таким образом, формула (1) не зависит от выбора системы ко­ординат на поверхности.

Изложенные соображения показывают разумность приведен­ного выше определения площади поверхности.

21. Интегралы по поверхности.

Пусть F — гладкая регулярная поверхность без самопересечений, заданная уравнением

— замкнутая ограниченная область, граница которой состоит из конечного числа простых замкнутых контуров. Обозна­чим часть поверхности F, определяемую множеством :

.

Пусть функция непрерывна в точках поверхности .

Определение. Поверхностный интеграл от функции по поверхности определяется равенством

(1)

где функции Е, F и G определяются формулами .

Очевидно, при сделанных относительно функции и поверхности F предположениях поверхностный интеграл первого рода всегда существует.

Замечание. В случае, когда поверхность задается урав­нением формула (1) принимает следую­щий вид:

Определение. Гладкая регулярная поверхность называет­ся ориентируемой, если на ней можно выбрать непрерывное поле единичных векторов нормали. В противном случае поверх­ность называется неориентируемой.

Поверхность, па которой выбрано непрерывное поле еди­ничных векторов нормали, называется ориентированной.

Очевидно, на гладкой регулярной поверхности без самопере­сечений существуют только два непрерывных поля единичных векторов нормали, а именно,

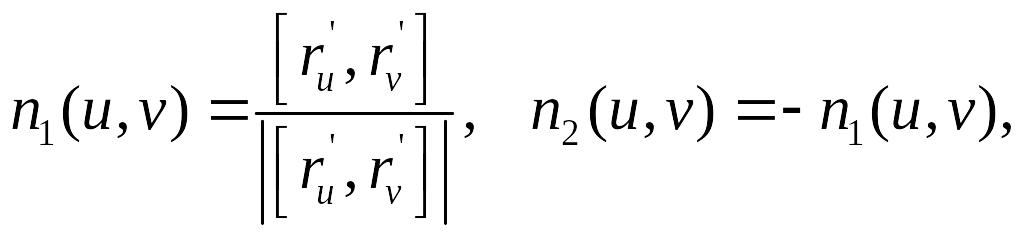
т. е. поверхность может быть ориентирована двумя различными

способами.

Замечание. Существуют неориентируемые поверхности. Простейшим примером такой поверхности является лист Мёбиуса. 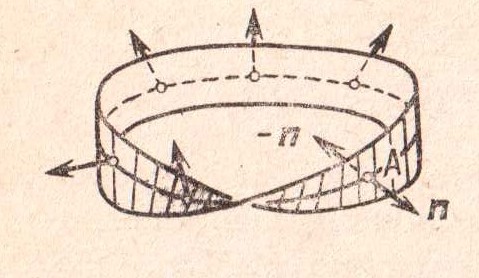Эту по­верхность можно получить, склеив два конца прямоугольной полоски бумаги, пред­варительно повернув один из них на 180°. При движении по «средней линии» ли­ста Мёбиуса, начиная с точки А, единич­ный вектор нормали непрерывно повора­чивается. По возвращении в точку А единичный вектор нормали, очевидно, изменит свое направление на противоположное. Поэтому на листе Мёбиуса нельзя, построите непрерывное поле единичных векторов нормали. Таким образом, лист Мёбиуса — неориентируемая поверхность.

Пусть гладкая регулярная поверхность без самопересечений ориентирована с помощью поля единичных векторов нормали

Пусть векторное поле

непрерывно на поверхности .

Определение. Потоком векторного поля через ориентированную поверхность называется интеграл вида

(2)

где поверхность определяется уравнением

.

Если поверхность ориентировать с помощью поля нормалей , то поток векторного поля (2) меняет знак.

При сделанных относительно векторного поля и по­верхности предположениях поверхностный интеграл (2) всегда существует.

Замечание. Если и поверхность задана урав­нением то

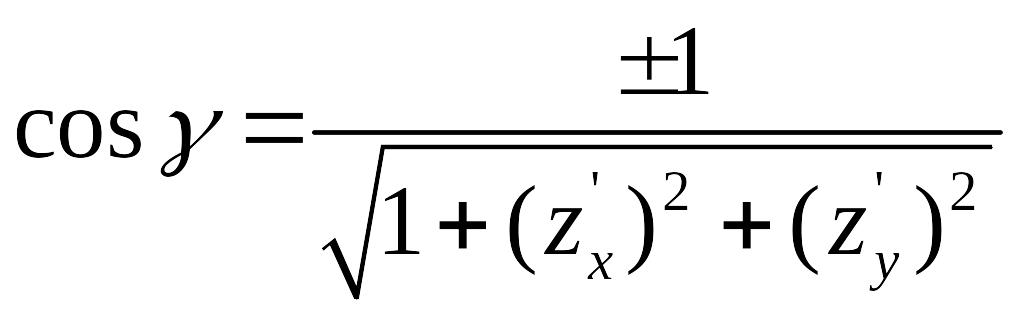
(знак зависит от выбора ориентации поверхности) и

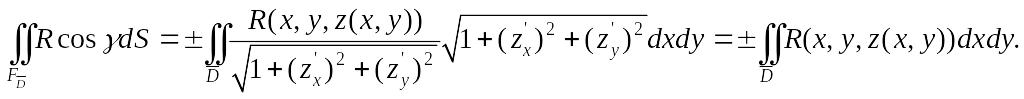
Эта формула оправдывает следующее обозначение:

По аналогичным соображениям интегралы

, обозначаются , соответственно. Полный поверхностный интеграл (2) обозначается так

В заключение параграфа распространим введенные нами понятия поверхностных интегралов на более широкий класс по­верхностей.

Определение. Поверхность называется кусочно гладкой регулярной поверхностью, если ее можно разбить на конечное число поверхностей таким образом, что:

1°. Каждая из поверхностей является частью некоторой

гладкой регулярной поверхности без самопересечений.

2°. Если поверхности , имеют общие точки, то эти точки лежат на кривых, ограничивающих и .

3°. Каждая из поверхностей имеет общий участок границы хотя бы с одной из поверхностей .

Поверхностный интеграл от непрерывной функции по кусочно гладкой регулярной поверхности определяется ра­венством

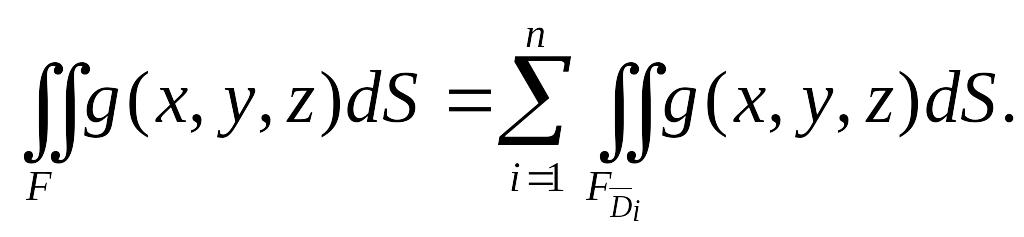
В частности, при интеграл

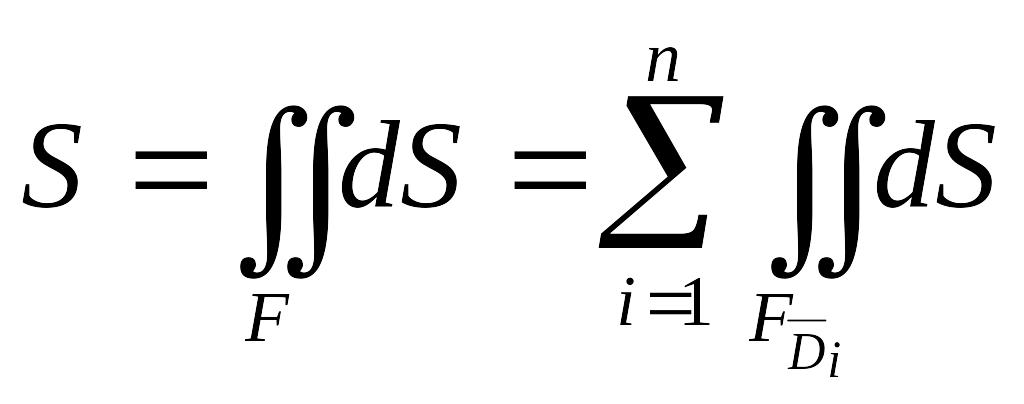
естественно назвать площадью поверхности .

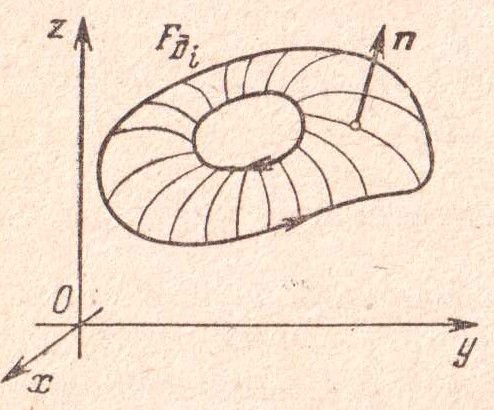
Сформулируем теперь правило ориентации контуров, ограничивающих поверхность : если, поверхность ориентирована, то каж­дый из контуров, ограничивающих эту поверхность, проходится таким обра­зом, что точки поверхности находятся слева от контура, если смотреть с конца вектора единичной нормали, определяющего ориентацию.

Определение. Кусочно гладкая регулярная поверхность называется ориентируемой, если каждую из поверхностей можно ориентировать так, чтобы все общие участки границы, принадлежащие различным поверхностям , , проходились

на них в различных направлениях.

Кусочно гладкая регулярная поверхность называется ориен­тированной, если каждая из поверхностей ориентирована в соответствии с условием, сформулированным выше.

Поток непрерывного векторного поля через ориенти­рованную кусочно гладкую регулярную поверхность определя­ется равенством