Вероятность ошибки приема флуктуирующих сигналов
Запишем сигнал на входе приемника в виде
(3.5)
Здесь = Sx / S0 – случайный мультипликативный коэффициент, Sx – случайная амплитуда, S0 – амплитуда в отсутствие замираний.
Тогда
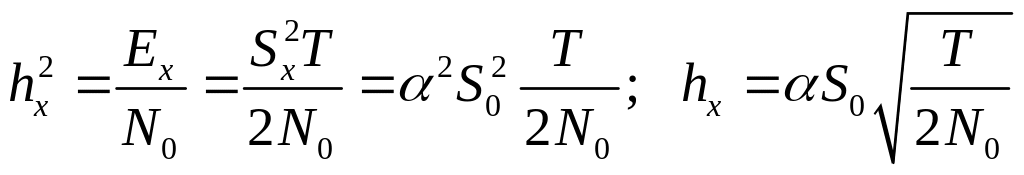(3.6)
Величина hx характеризует ОСШ принятого в данный момент времени символа. Вероятность ошибки при этом обозначим как PE(hx). Необходимо найти среднюю за сеанс связи вероятность ошибки. Математическое ожидание М[PE(hx)] ищем обычным образом:
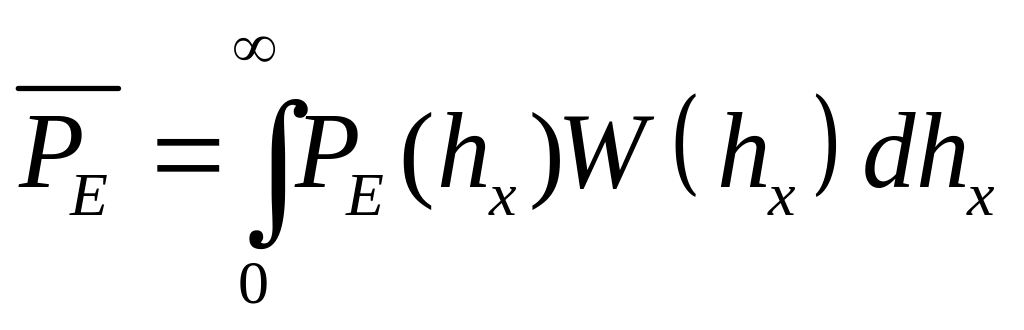, (3.7)
где
W(hx)
– неизвестное пока распределение
случайной величины hx.
Будем предполагать, что канал является
релеевским, т.е. амплитуда Sx
распределена по релеевскому закону.
Связь между величинами hx
и Sx
дает соотношение (3.6). Представим его в
виде
,
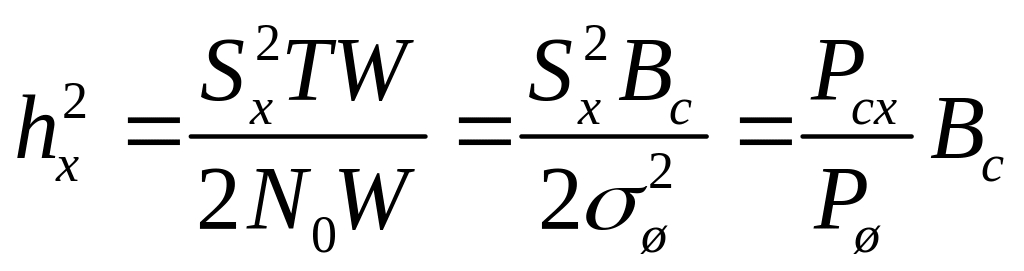или
= aSx, (3.8)
где Bc
= WT – база сигнала,
- мощность шума, Pcx
– мощность принятого сигнала.
Распределение случайной амплитуды запишем в виде:
,
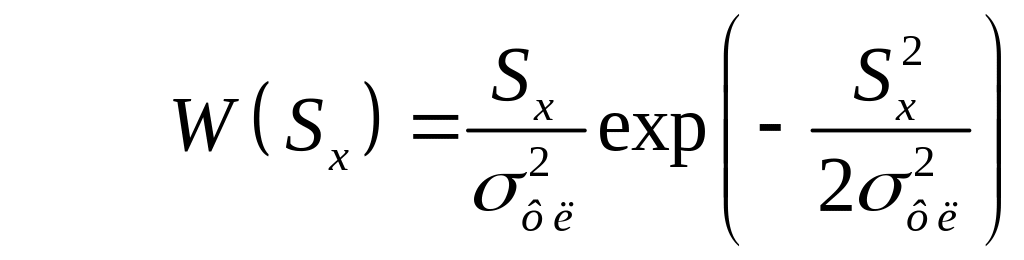(3.9)
где
- мощность флуктуирующей составляющей.
Воспользуемся теоремой о функциональном преобразовании распределений случайных величин, которая в данном контексте выглядит, как
W(y) = Wx[(y)] [(y)], где:
y=f(x) – связь между старой и новой случайными величинами x и y: hx = aSx, (y) – функция, обратная f(x): Sx = hx / a,
Wx(x) – плотность распределения вероятностей случайной величины x. Тогда:
(3.10)
В последнем соотношении использовано
равенство средней энергии посылки
флуктуирующего сигнала и энергии посылки
сигнала в отсутствии флуктуаций, что
следует из физических соображений.
Говоря другими словами,
.
Окончательно, искомую плотность распределения запишем в виде
(3.11)
Теперь имеется все необходимое для вычисления вероятности ошибки в каналах со случайными параметрами. Для получения удобной сокращенной записи введем коэффициент с, учитывающий тип используемых сигналов:
с =
для противоположных сигналов,
с = 1 для ортогональных сигналов,
с = 1/ для сигналов БАМ
Когерентный прием двоичных сигналов
Среднее значение вероятности ошибки в соответствии с (3.7) ищем в виде
(3.12)
Интеграл (3.12) берем по частям, воспользовавшись правилом udv = uv - vdu.
В нашем случае
u = Q(chx), dv = exp(-hx2/h2)d(hx2/h2);
,
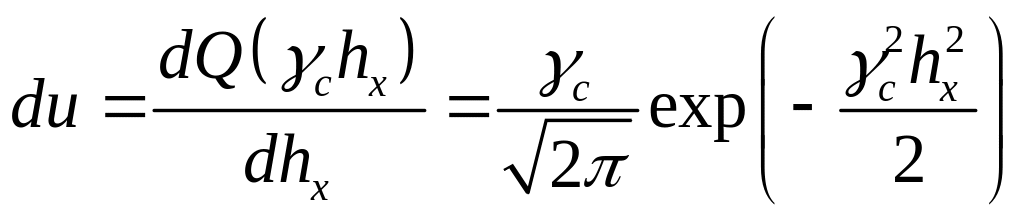v = exp(-hx2/h2).
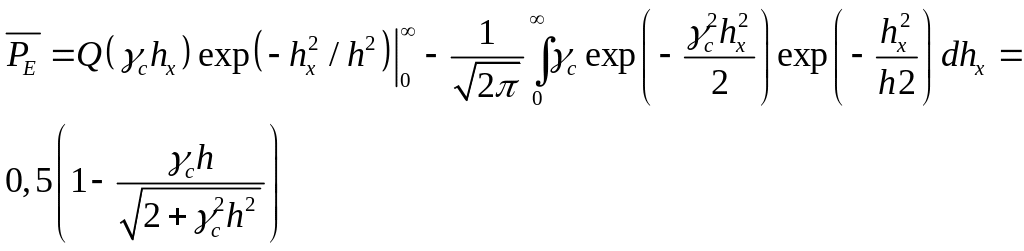(3.13)
При вычислении (3.13) использован табличный интеграл [6]
Цифровые системы связи должны работать с вероятностями ошибок PE 10-3, что обеспечивается отношением сигнал/шум h 3. В этом случае
(3.14)
и для различных типов манипуляции получаем:
для сигналов БАМ;
для сигналов БЧМ;
для сигналов БФМ.
Некогерентный прием двоичных сигналов
Ранее были получены выражения для вероятности ошибки некогерентного приема сигналов БАМ и БЧМ (2.56) и (2.58). Объединяя их с помощью коэффициента с, получим заменой h на hx:
PE(hx) = 0,5 exp(-c2hx2/2) (3.15)
Проделав вычисления, аналогичные разделу 3.1.1, получим выражения для средней вероятности ошибки в канале со случайными параметрами:
, (3.16)
которое упрощается для больших отношений сигнал/шум до
. (3.17)
Для различных типов манипуляции будем иметь:
для сигналов БАМ;
для сигналов БЧМ;
для сигналов БФМ.
Весьма поучительно сравнение затрат энергии для получения вероятности ошибок, не превышающих 10-5, при отсутствии и наличии замираний, которое представлено таблицей 3.1.
Таблица 3.1
-
Сигнал
h2
Гауссовский
Релеевский
БАМ
45
2105
БЧМ
22
105
БФМ
11
5104
Из приведенных в таблице расчетных данных следует, что без принятия специальных мер некогерентный прием при наличии замираний требует огромных энергетических затрат, совершенно неприемлемых в практической реализации. Поэтому рассмотрим далее методы, применяемые для борьбы с замираниями.