
1.5. Колебания и волны
Основные характеристики колебательного движения. Гармонические колебания. Собственные и вынужденные колебания. Резонанс. Природа звука. Физические основы речи и слуха человека. Характеристики слухового ощущения и их связь с физическими характеристиками звука. Аудиометрия. Фонокардиография. Инфразвук и ультразвук. Физические основы сейсмологии. Природные источники инфразвука и ультразвука (землетрясение, шторм, цунами). Действие инфразвука и ультразвука на биологические объекты. Медико-биологическое использование ультразвука.
5.1. Гармоническое колебание и его характеристики
Колебательным движением (колебанием) называется процесс, при котором система, многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему. Если этот возврат совершается через равные промежутки времени, то колебание называется периодическим. Наглядным примером колебания может служить движение часового маятника. Колебательные движения исключительно широко распространены в природе и технике. Вибрация натянутой струны, движение поршня дизеля и ножей косилки, суточные и годичные изменения температуры воздуха, морские
приливы и отливы, волнение водной поверхности, биение сердца, дыхание, тепловое движение ионов кристаллической решетки твердого тела, переменный ток и его электромагнитное поле, движение электронов в атоме
и т. д. — все это в конечном счете колебательные процессы. Несмотря на большое разнообразие колебательных процессов как по физической при-
природе, так и по степени сложности, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими.
С основными
закономерностями и характеристиками
гармонического колебания проще всего
познакомиться на примере равномерного
движения материальной точки по окружности.
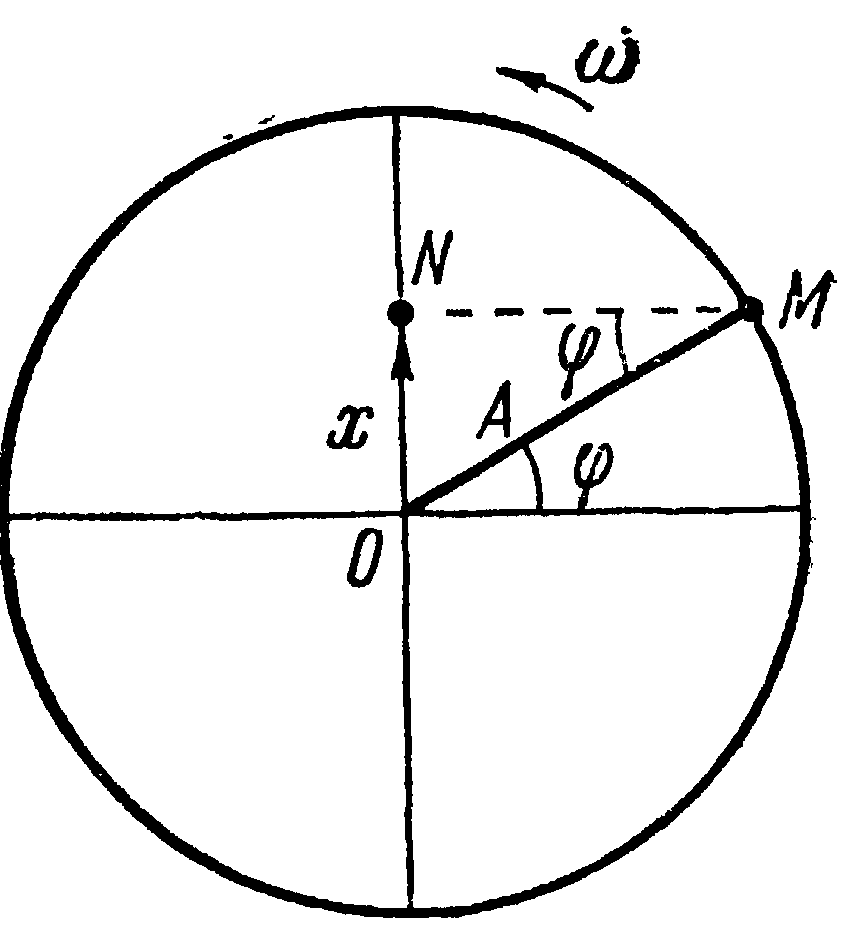
Пусть материальная точка М
движется
против часовой стрелки по окружности
радиусом А
с постоянной угловой скоростью
![]() (рис. 5.1). Тогда ее проекция N
на вертикальный диаметр будет совершать
периодические колебания около положения
равновесия О,
а величина смещения этой проекции (
(рис. 5.1). Тогда ее проекция N
на вертикальный диаметр будет совершать
периодические колебания около положения
равновесия О,
а величина смещения этой проекции (![]() )
изменяться в пределах от +А
до -А,
также совершая периодические колебания.
Величина смещения в любой момент времени
)
изменяться в пределах от +А
до -А,
также совершая периодические колебания.
Величина смещения в любой момент времени
![]() определяется очевидным соотношением
определяется очевидным соотношением
![]() (1)
(1)
Так как период
вращения материальной точки
![]() ,
число ее оборотов в секунду
,
число ее оборотов в секунду
![]() ,
угловая скорость
и угол поворота радиуса
,
угловая скорость
и угол поворота радиуса
![]() связаны между собой соотношениями:
связаны между собой соотношениями:
![]()
 Рисунок
5.1.
Рисунок
5.1.
то формулу (1) можно написать еще так:
![]() (2)
(2)
![]() (2а)
(2а)
![]() (2б).
(2б).
Соотношения (1) — (2б) являются разновидностями уравнения гармонических колебаний. Следовательно, гармоническим называется колебание, при котором изменение колеблющейся величины со временем происходит по закону синуса (или косинуса, если точка М проецируется на горизонтальной диаметр). Смещение х положительно, когда направлено вверх от положения равновесия, и отрицательно, когда направлено вниз. Абсолютное значение максимального смещения А называется амплитудой колебания.
При описании колебательных процессов физические величины , , и принято называть иначе, чем мы называли их ранее: называется периодом колебания, - частотой колебания, - круговой, или циклической частотой и - фазой колебания. Единицы измерения этих величин остаются, конечно, прежними.
Фазой колебания
![]() называется аргумент тригонометрической
функции в уравнении гармонического
колебания. Физический смысл фазы состоит
в том, что она определяет смещение в
любой момент времени, т. е. определяет
состояние колебательной системы.
Действительно, например, при
называется аргумент тригонометрической
функции в уравнении гармонического
колебания. Физический смысл фазы состоит
в том, что она определяет смещение в
любой момент времени, т. е. определяет
состояние колебательной системы.
Действительно, например, при
![]() смещение
смещение
![]() ,
при
,
при
![]()
![]() ,
при
,
при
![]()
![]() и т.п. Из уравнения (1) следует, что фазам,
различающимся между собой на величину,
кратную
и т.п. Из уравнения (1) следует, что фазам,
различающимся между собой на величину,
кратную
![]() ,
соответствуют одинаковые смещения.
Изменение фазы на
рад соответствует промежутку времени
в один период
.
,
соответствуют одинаковые смещения.
Изменение фазы на
рад соответствует промежутку времени
в один период
.
Колебательное движение реальной механической системы всегда сопровождается трением, на преодоление которого расходуется часть энергии колебательной системы. Поэтому энергия колебания в процессе колебания уменьшается, переходя в теплоту. Так как энергия колебания пропорциональна квадрату амплитуды
![]() ,
,
где
![]() - амплитуда,
-
круговая частота колебаний, то постепенно
уменьшается и амплитуда колебаний.
Когда вся энергия колебания перейдет
в теплоту, колебание прекратится
(затухнет). Такого рода колебания
называются затухающими.
- амплитуда,
-
круговая частота колебаний, то постепенно
уменьшается и амплитуда колебаний.
Когда вся энергия колебания перейдет
в теплоту, колебание прекратится
(затухнет). Такого рода колебания
называются затухающими.
Для того чтобы система совершала незатухающие колебания, необходимо восполнять извне потери энергии колебания на трение. Для этого надо воздействовать на систему периодически изменяющейся силой
![]()
где
![]() —
амплитудное (максимальное) значение
силы,
— круговая частота колебаний силы,
—
время. Внешняя сила, обеспечивающая
незатухающие колебания системы,
называется вынуждающей силой, а колебания
системы — вынужденными.
Очевидно, что вынужденные колебания
происходят с частотой, равной частоте
вынуждающей силы.
—
амплитудное (максимальное) значение
силы,
— круговая частота колебаний силы,
—
время. Внешняя сила, обеспечивающая
незатухающие колебания системы,
называется вынуждающей силой, а колебания
системы — вынужденными.
Очевидно, что вынужденные колебания
происходят с частотой, равной частоте
вынуждающей силы.
Амплитуда вынужденного колебания
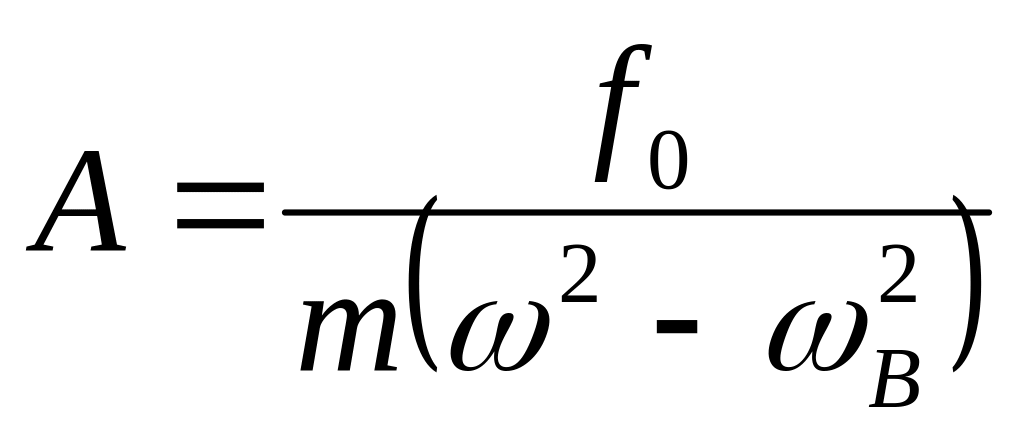
зависит от
соотношения круговых частот вынужденного
и собственного колебаний: при
![]() будет
будет
![]() и
и
![]() .
.
В действительности
благодаря трению амплитуда вынужденных
колебаний остается конечной. Она
достигает максимального значения в том
случае, когда частота вынужденных
колебаний близка к частоте собственных
колебаний системы. Явление резкого
возрастания амплитуды вынужденных
колебаний при
![]() называется резонансом.
называется резонансом.
5.2. Характеристики звуковой волны.
Колебания частиц в упругих средах, распространяющиеся в форме продольных волн, частота которых лежит в пределах, воспринимаемых человеческим ухом, т. е. в среднем от16 до20000 Гц, называются звуковыми колебаниями или просто звуком.
Волна называется поперечной, если частицы среды колеблются перпендикулярно к лучу. Если же они колеблются вдоль луча, то волна называется продольной.
Звуки разделяются на тоны и шумы. Тоном называется звук, который представляет регулярное колебание с постоянными или закономерно изменяющимися по времени амплитудой и частотой. В зависимости от формы колебания частиц среды тоны подразделяются на простые (гармонические) и сложные. Простой (или гармонический) тон может быть получен с помощью камертона или звукового генератора. К сложным тонам относятся, например, звуки музыкальных инструментов, гласные звуки речи человека и др.
Звуковой тон характеризуется частотой (или периодом), амплитудой и формой колебания или его гармоническим спектром, а также величинами, относящимися к звуковой волне: интенсивностью или силой звука и звуковым давлением.
Интенсивностью
или силой
звука называют
плотность потока энергии звуковой
волны; единицы измерения – 1
![]() ,
1
,
1
![]() ,
а также 1
,
а также 1
![]() .
.
Звуковым или
акустическим давлением
![]() называют
эффективное (среднеквадратическое)
значение добавочного давления (избыточного
над средним давлением окружающей среды),
образующегося в участках сгущения
частиц в звуковой волне. Оно выражается
в ньютонах на квадратный метр (
называют
эффективное (среднеквадратическое)
значение добавочного давления (избыточного
над средним давлением окружающей среды),
образующегося в участках сгущения
частиц в звуковой волне. Оно выражается
в ньютонах на квадратный метр (![]() ).
).
Для плоской
гармонической волны звуковое давление
связано с интенсивностью звука
![]() соотношением
соотношением
![]() ,
где
,
где
![]() -
плотность среды,
-
плотность среды,
![]() -
скорость звука.
-
скорость звука.
Звук, свободно распространяющийся в среде, представляет собой бегущую волну. В ограниченных участках среды образуются стоячие звуковые волны. При совпадении или кратном отношении частоты колебаний звуковой волны и собственной частоты участка среды амплитуда колебаний резко возрастает, это явление называют звуковым резонансом и используют для усиления звука. Звуковыми резонаторами обычно служат воздушные столбы, заполняющие полости соответствующих размеров и формы. Если на резонатор попадает сложная звуковая волна, то в ней усиливаются только гармонические тоны, частоты которых совпадают или кратны собственной частоте резонатора.
