5.3 Кут між прямою і площиною.

Н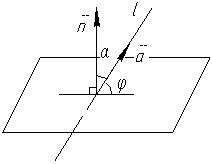 ехай - кут між прямою і площиною , - кут між нормальним вектором площини і напрямним вектором прямої

Кут між прямою і площиною знаходять за формулою

Умова паралельності прямої і площини :

Умова перпендикулярності прямої і площини :

5.4 Окремі випадки завдання площини у просторі

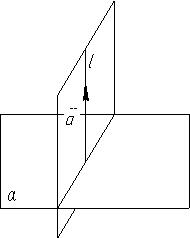
5.4.1 Рівняння площини, яка проходить через задану пряму, перпендикулярно до заданої площини.

Нехай пряма задана рівнянням , а площина задана рівнянням причому . Тоді рівняння має вигляд:

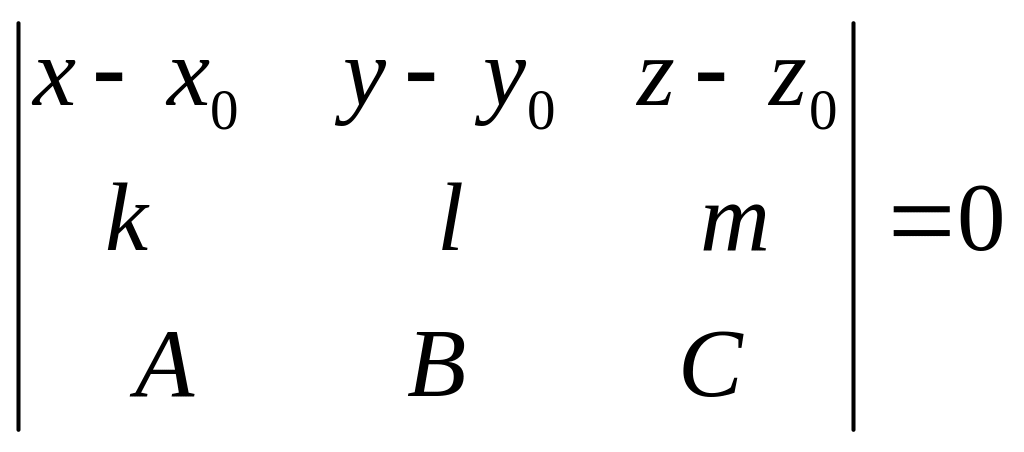
5.4.2 Рівняння площини, яка проходить через дві паралельні прямі.

Дві паралельні прямі і задані відповідно рівняннями

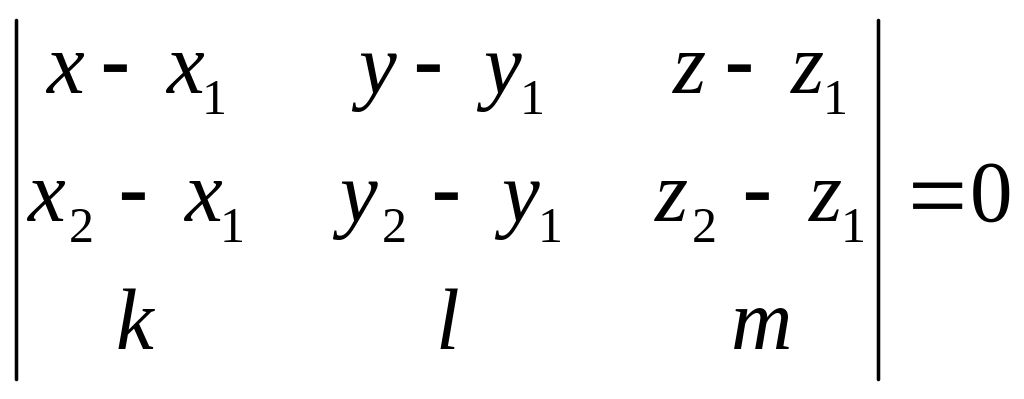- рівняння шуканої площини.

5.4.3 Рівняння площини, яка проходить через дві прямі, що перетинаються.

Дві прямі, що перетинаються і задані відповідно рівняннями

Т оді:

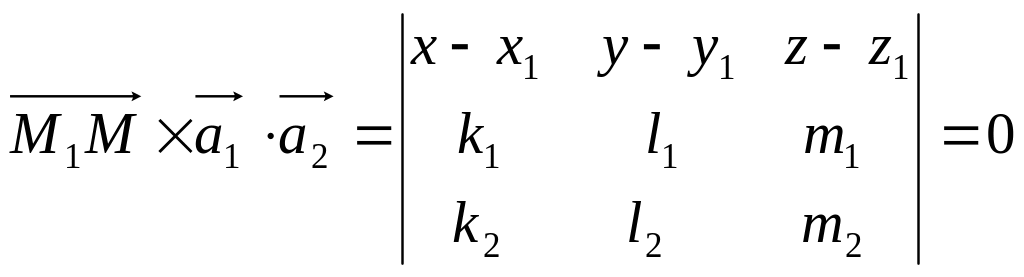- рівняння

шуканої площини.

5.4.4 Рівняння площини, яка проходить через задану пряму і задану точку.

Дана пряма задана рівнянням і точка ( ) .

Тоді:

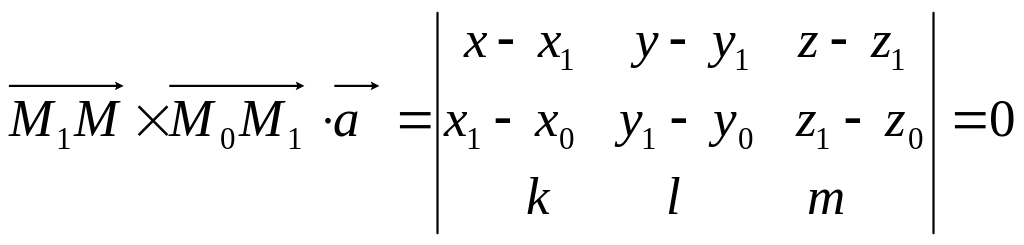- рівняння шуканої площини.

Контрольні запитання.

5. Запишіть загальне рівняння площини. Зробіть його досліження.

6. Які умови паралельності та перпендикулярності площин?

7. Запишіть рівняння площини, що проходить через три точки.

8. Запишіть види рівнянь прямої у просторі.

9. Як знайти кут між прямою і площиною?

10. Запишіть рівняння площини, яка проходить через дві паралельні прямі.

11. Запишіть рівняння площини, яка проходить через дві прямі, що перетинаються.

12. Запишіть рівняння площини, яка проходить через задану пряму і задану точку.

Лекція 6. Криві другого порядку. Поверхні другого порядку

План.

1. Вступ.

2. Еліпс (*).

3. Гіпербола (*).

4. Парабола (*).

5. Поверхні другого порядку (*).

6.1 Вступ.

Кривою другого порядку називається множина М точок площини, координати яких задовольняють рівняння другого степеня

, де - дійсні числа.

До кривих другого порядку відносяться: коло, еліпс, гіпербола, парабола.

Коло – це геометричне місце точок, кожна з яких рівновіддалена від даної точки, яка називається центром кола.

, точка - центр кола.

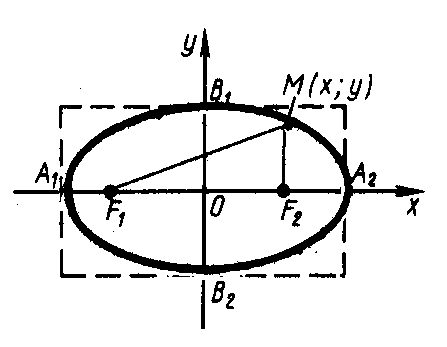
6.2 Еліпс.

Еліпс – це геометричне місце точок площини, сума відстаней від кожної з яких до двох заданих точок, які називаються фокусами, є величина стала і дорівнює 2а.

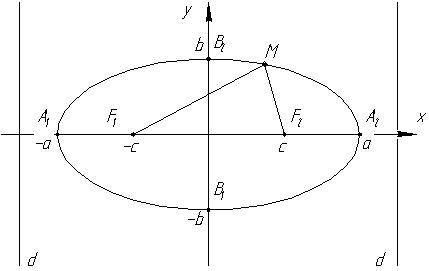
Точка - належить еліпсу, і - фокуси, і - фокусні радіуси точки М.

За означенням

Позначимо , тоді .

Поділимо обидві частини цієї рівності на , тоді

- канонічне рівняння еліпса.

2а – велика вісь, 2в – мала вісь, 2с – фокусна вісь, - вершини еліпса

зв’язок між фокусною відстанню та осями еліпса ( ).

Ексцентриситетом еліпса називається відношення фокусної відстані до більшої осі: . Ексцентриситет вказує на форму еліпса.

Директрисами еліпса називаються прямі, що задаються рівнянням: .

- рівняння еліпса із зміщеним центром, - центр.

Канонічне рівняння
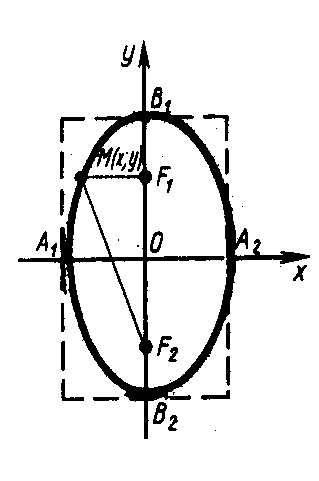
Розташування фокусів Координати фокусів Співвідношення між a і b Велика вісь Мала вісь Фокусна відстань Ексцентриситет Співвідношення між a,b,c	F1 ; F2  Ox F­1(-c;0), F2(c;0) a>b |A1A2|=2a |B1B2|=2b |F1F2|=2c =c/a a2 - b2 = с2	F1 ; F2  Oy F­1(0;c), F2(0;-c) a<b |B1B2|=2b |A1A2|=2a |F1F2|=2c =c/b b2 - a2 = с2