
- •1.Основные гипотезы о свойствах материалов.
- •2. Внутренние силовые факторы в статически определимых нагруженных конструкциях (усилия и моменты) и методы их определения.
- •3. Виды и обозначения напряжений и деформаций. Правило знаков. Закон Гука при растяжении и сдвиге.
- •4. Методы механических испытаний материалов.
- •5. Типовые диаграммы растяжения и сжатия пластичных и хрупких материалов. Деформационное упрочнение (наклёп). Эффект Баушингера.
- •6. Механические хар-ки материала (предел упругости, текучести, прочности, модуль Юнга, коэффициент Пуассона).
- •7. Инженерные методы расчёта на прочность (по допускаемым напряжениям, предельным состояниям (расчётным сопротивлениям), разрушающим нагрузкам).
- •8. Внутренние усилия, напряжения и деформации при растяжении стержней. Правила построения эпюр. Расчёты на прочность.
- •9. Потенциальная энергия деформации при растяжении-сжатии.
- •10. Напряжения на наклонных площадках при растяжении и сжатии.
- •11. Статически неопределимые задачи при растяжении и сжатии. Метод решения.
- •12. Монтажные, влажностные и термические напряжения и деформации. Учёт ползучести.
- •15. Потенциальная энергия деформации при сдвиге.
- •14. Сдвиг и срез. Инженерные методы расчётов на прочность.
- •13. Напряжения и деформации при сдвиге. Закон парности касательных напряжений.
- •16. Определение геометрических характеристик сечений (статические моменты, осевые, полярные и центробежные моменты инерции, моменты сопротивления).
- •17. Центр тяжести сечения. Метод определения. Понятие о центральных осях.
- •18. Зависимость между моментами инерции относительно параллельных осей.
- •19. Вычисление моментов инерции простейших фигур (прямоугольник, круг).
- •20. Порядок вычисления моментов инерции сложных фигур. Главные оси и главные моменты инерции.
- •21. Напряжения при кручении цилиндрического бруса круглого сечения.
- •22. Деформации при кручении цилиндрического бруса круглого сечения.
- •23. Потенциальная энергия деформации при кручении.
- •24. Кручение тонкостенного бруса замкнутого профиля.
- •25. Распределение напряжений по сечению при кручении бруса прямоугольного сечения.
- •26. Расчёты на прочность и жёсткость при кручении.
- •27. Расчёт цилиндрических винтовых пружин малого шага.
- •28. Статически неопределимые задачи при кручении.
- •29. Внутренние силовые факторы при изгибе бруса.
- •30. Дифференциальные зависимости между силовыми факторами при изгибе.
- •31. Правила построения эпюр поперечных сил и изгибающих моментов.
- •36. Потенциальная энергия деформации при изгибе.
- •35. Напряжения при изгибе тонкостенных балок. Центр изгиба.
- •34. Расчёты на прочность при поперечном изгибе.
- •33. Касательные напряжения при поперечном изгибе. Формула Журавского.
- •32. Нормальные напряжения при чистом изгибе. Рациональные формы поперечных сечений балок.
- •37. Перемещения при изгибе. Диф. Ур. Упругой линии и его интегрирование.
- •38. Перемещения при изгибе. Метод начальных параметров.
- •39. Энергетический метод определения перемещений сечений балок. Интеграл Мора.
- •40. Способ Верещагина. Формула Симпсона.
5. Типовые диаграммы растяжения и сжатия пластичных и хрупких материалов. Деформационное упрочнение (наклёп). Эффект Баушингера.
Диаграмма растяжения пластичных материалов:
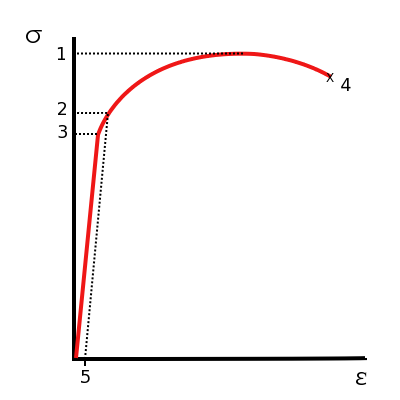
Диаграмма растяжения хрупких материалов:
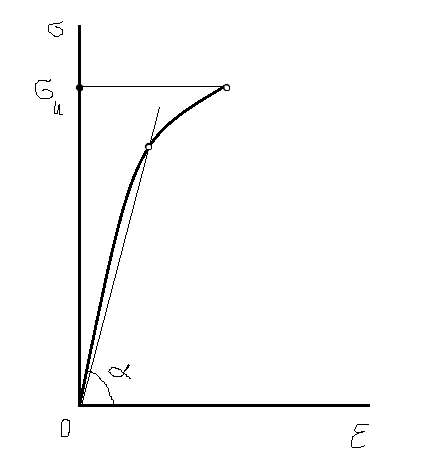
Наклёп — упрочнение поверхности металлов и сплавов вследствие изменения их структуры и фазового состава в процессе пластической деформации, при температуре ниже температуры рекристаллизации. Наклёп сопровождается выходом на поверхность образца дефектов кристаллической решётки, увеличением прочности и твёрдости и снижением пластичности, ударной вязкости, сопротивления металлов деформации противоположного знака.
Различают два вида наклёпа: фазовый и деформационный. Деформационный наклёп является результатом действия внешних деформационных сил. При фазовом наклёпе источником деформаций служат фазовые превращения, в результате которых образуются новые фазы с отличным от исходных удельными объёмами.
Увеличение предела текучести материала при растяжении приводит к уменьшению его при сжатии. Подобное изменение механических характеристик материала после пластического деформирования носит название эффекта Баушингера.
6. Механические хар-ки материала (предел упругости, текучести, прочности, модуль Юнга, коэффициент Пуассона).
Механическими характеристиками конструкционных материалов называются величины, характеризующие их прочность, пластичность, твёрдость и т.д., а также модули упругости и коэффициент Пуассона.
Предел упругости — максимальная величина механического напряжения, при которой деформация данного материала остаётся упругой, то есть полностью исчезает после снятия нагрузки.
Предел
текучести
— механическое напряжение
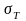 ,
отвечающее нижнему положению площадки
текучести на диаграмме деформирования
материала. Предел
прочности
— механическое напряжение
,
отвечающее нижнему положению площадки
текучести на диаграмме деформирования
материала. Предел
прочности
— механическое напряжение
 ,
выше которого происходит разрушение
материала.
,
выше которого происходит разрушение
материала.
Модуль Юнга (модуль упругости) — коэффициент, характеризующий сопротивление материала растяжению/сжатию при упругой деформации.
Модуль
Юнга рассчитывается следующим образом:![]() ,
где
,
где
E — модуль упругости, измеряемый в паскалях
F — сила в ньютонах,
S — площадь поверхности, по которой распределено действие силы,
l — длина деформируемого стержня,
x — модуль изменения длины стержня в результате упругой деформации.
Коэффициент Пуассона (обозначается как ν или μ) характеризует упругие свойства материала. Коэф. показывает, во сколько раз изменяется поперечное сечение деформируемого тела при его растяжении или сжатии. Для абсолютно хрупкого материала коэф. = 0, для абсолютно упругого = 0,5.
Диаграмма сжатия пластичных материалов:
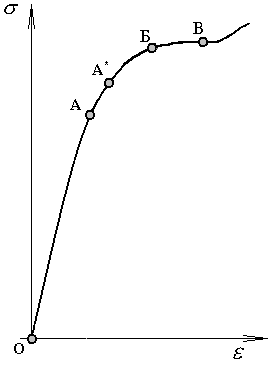
Диаграмма сжатия хрупких материалов:

7. Инженерные методы расчёта на прочность (по допускаемым напряжениям, предельным состояниям (расчётным сопротивлениям), разрушающим нагрузкам).
Можно выделить три основных метода расчёта элементов конструкций или деталей машин на прочность при силовых воздействиях:
1. По допускаемым напряжениям
У
пластичных материалов опасное состояние
хар-ся появлением значительных
пластических деформаций, у хрупких –
возникновением трещин. Для каждого
материала устанавливается опасное
(предельное) напряжение
 .
Далее определяется допускаемое
напряжение:
.
Далее определяется допускаемое
напряжение:
 .
Где
.
Где
 -
коэф. запаса прочности.
-
коэф. запаса прочности.
Условие
прочности имеет вид:
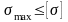 ,
где
,
где
 -
наибольшее по абсолютной величине
напряжение в конструкции.
-
наибольшее по абсолютной величине
напряжение в конструкции.
2. По допускаемым нагрузкам (по разрушающим нагрузкам)
Метод расчёта по допускаемым нагрузкам предполагает определение расчётным путём не напряжений, а максимальной нагрузки, которую может выдержать конструкция, не разрушаясь и не претерпевая непрерывно нарастающих пластических деформ. В основу метода положено условие предельного равновесия системы, т.е. установление предельного значения внешней нагрузки, которая может быть уравновешена внутренними силами.
3. По предельным состояниям
Предельное состояние – такое состояние конструкции, когда она теряет способность к сопротивлению внешним нагрузкам или её эксплуатация становится затруднительной.
Метод расчёта по предельным состояниям позволяет производить прочностные расчёты конструкций как в предположении упругой работы материала, так и с учётом пластических деформаций.
8. Внутренние усилия, напряжения и деформации при растяжении стержней. Правила построения эпюр. Расчёты на прочность.
Принцип Сен-Венана: в сечениях, достаточно удаленных от мест приложения сил, распределение напряжений и деформаций мало зависит от способа приложения нагрузок.
Принцип Сен-Венана дает возможность вести расчет без учета местных (локальных) деформаций, возникающих вблизи точек приложения внешних сил и отличающихся от деформаций основного объема материала, что в большинстве случаев упрощает решение задачи.
Гипотеза плоских сече-ний (гипотеза Я.Бернулли): поперечные сечения стержня плоские и перпендикулярные его оси до деформации остаются плоскими и перпендикулярными оси, и после деформации.
Мысленно рассекая стержень, определим внутренние силы в растянутом стержне:
а) стержень, нагруженный растягивающими силами F и находящийся в равновесии, рассекаем произвольным сечением;
б) отбрасываем одну из частей стержня, а ее действие на другую часть компенсируем внутренними усилиями интенсивностью ;
в)
осевое внутреннее
усилие N,
возникающее в сечении стержня,
определим,
составляя уравнения равновесия для
отсеченной части: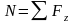 .
.
Проецируя внешнюю силу F, действующую на отсеченную часть стержня, на другие оси (x и y), а также составляя уравнения моментов относительно координатных осей, легко убедится, что осевое усилие N является единственным внутренним усилием, возникающим в сечении стержня (остальные тождественно равны нулю).
Таким образом, при растяжении (сжатии) из шести внутренних усилий в сечении стержня возникает только одно — продольная сила N.
7
4
8
9
10
12
